Question 1. Define a function as a set of ordered pairs.
Solution:
Let A and B be two non-empty sets. A relation from A to B, i.e., a subset of A×B, is called a function (or a mapping) from A to B, if
(i) for each a ∈ A there exists b ∈ B such that (a, b) ∈ f
(ii) (a, b) ∈ f and (a, c) ∈ f ⇒ b = c
Question 2. Define a function as a correspondence between two sets.
Solution:
Let A and B be two non-empty sets. Then a function ‘f’ from set A to B is a rule or method or correspondence which associates elements of set A to elements of set B such that:
(i) all elements of set A are associated to elements in set B.
(ii) an element of set A is associated to a unique element in set B.
Question 3. What is the fundamental difference between a relation and a function? Is every relation a function?
Solution:
Let ‘f’ be a function and R be a relation defined from set X to set Y.
The domain of the relation R might be a subset of the set X, but the domain of the function f must be equal to X. This is because each element of the domain of a function must have an element associated with it, whereas this is not necessary for a relation.
In relation, one element of X might be associated with one or more elements of Y, while it must be associated with only one element of Y in a function.
Thus, not every relation is a function. However, every function is necessarily a relation.
Question 4. Let A = {–2, –1, 0, 1, 2} and f: A → Z be a function defined by f(x) = x2 – 2x – 3. Find:
(i) range of f i.e. f (A)
(ii) pre-images of 6, –3 and 5
Solution:
Given:
A = {–2, –1, 0, 1, 2}
f : A → Z such that f(x) = x2 – 2x – 3
(i) Range of f i.e. f (A)
A is the domain of the function f. Hence, range is the set of elements f(x) for all x ∈ A.
Substituting x = –2 in f(x), we get
f(–2) = (–2)2 – 2(–2) – 3
= 4 + 4 – 3
= 5
Substituting x = –1 in f(x), we get
f(–1) = (–1)2 – 2(–1) – 3
= 1 + 2 – 3
= 0
Substituting x = 0 in f(x), we get
f(0) = (0)2 – 2(0) – 3
= 0 – 0 – 3
= – 3
Substituting x = 1 in f(x), we get
f(1) = 12 – 2(1) – 3
= 1 – 2 – 3
= – 4
Substituting x = 2 in f(x), we get
f(2) = 22 – 2(2) – 3
= 4 – 4 – 3
= –3
Thus, the range of f is {-4, -3, 0, 5}.
(ii) pre-images of 6, –3 and 5
Let x be the pre-image of 6
⇒ f(x) = 6
x2 – 2x – 3 = 6
x2 – 2x – 9 = 0
x = [-(-2) ± √ ((-2)2 – 4(1) (-9))] / 2(1)
= [2 ± √ (4+36)] / 2
= [2 ± √40] / 2
= 1 ± √10
However, 1 ± √10 ∉ A
Thus, there exists no pre-image of 6.
Now, let x be the pre-image of –3
⇒ f(x) = –3
x2 – 2x – 3 = –3
x2 – 2x = 0
x(x – 2) = 0
x = 0 or 2
Clearly, both 0 and 2 are elements of A.
Thus, 0 and 2 are the pre-images of –3.
Now, let x be the pre-image of 5
⇒ f(x) = 5
x2 – 2x – 3 = 5
x2 – 2x – 8= 0
x2 – 4x + 2x – 8= 0
x(x – 4) + 2(x – 4) = 0
(x + 2)(x – 4) = 0
x = –2 or 4
However, 4 ∉ A but –2 ∈ A
Thus, –2 is the pre-images of 5.
∴ Ø, {0, 2}, -2 are the pre-images of 6, -3, 5
Question 5. If a function f: R → R be defined by
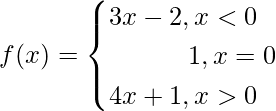
Find: f (1), f (–1), f (0), f (2).
Solution:
Given:
Let us find f (1), f (–1), f (0) and f (2).
When x > 0, f (x) = 4x + 1
Substituting x = 1 in the above equation, we get
f (1) = 4(1) + 1
= 4 + 1
= 5
When x < 0, f(x) = 3x – 2
Substituting x = –1 in the above equation, we get
f (–1) = 3(–1) – 2
= –3 – 2
= –5
When x = 0, f(x) = 1
Substituting x = 0 in the above equation, we get
f (0) = 1
When x > 0, f(x) = 4x + 1
Substituting x = 2 in the above equation, we get
f (2) = 4(2) + 1
= 8 + 1
= 9
∴ f (1) = 5, f (–1) = –5, f (0) = 1 and f (2) = 9.
Question 6. A function f: R → R is defined by f(x) = x2. Determine
(i) range of f
(ii) {x: f(x) = 4}
(iii) {y: f(y) = –1}
Solution:
Given:
f : R → R and f(x) = x2.
(i) range of f
Domain of f = R (set of real numbers)
We know that the square of a real number is always positive or equal to zero.
∴ range of f = R+∪ {0}
(ii) {x: f(x) = 4}
Given:
f(x) = 4
we know, x2 = 4
x2 – 4 = 0
(x – 2)(x + 2) = 0
∴ x = ± 2
∴ {x: f(x) = 4} = {–2, 2}
(iii) {y: f(y) = –1}
Given:
f(y) = –1
y2 = –1
However, the domain of f is R, and for every real number y, the value of y2 is non-negative.
Hence, there exists no real y for which y2 = –1.
∴{y: f(y) = –1} = ∅
Question 7. Let f: R+→ R, where R+ is the set of all positive real numbers, be such that f(x) = loge x. Determine
(i) the image set of the domain of f
(ii) {x: f (x) = –2}
(iii) whether f (xy) = f (x) + f (y) holds.
Solution:
Given f: R+→ R and f(x) = loge x.
(i) the image set of the domain of f
Domain of f = R+ (set of positive real numbers)
We know the value of logarithm to the base e (natural logarithm) can take all possible real values.
∴ The image set of f = R
(ii) {x: f(x) = –2}
Given f(x) = –2
loge x = –2
∴ x = e-2 [since, logb a = c ⇒ a = bc]
∴ {x: f(x) = –2} = {e-2}
(iii) Whether f (xy) = f (x) + f (y) holds.
We have f (x) = loge x ⇒ f (y) = loge y
Now, let us consider f (xy)
F (xy) = loge (xy)
f (xy) = loge (x × y) [since, logb (a×c) = logb a + logb c]
f (xy) = loge x + loge y
f (xy) = f (x) + f (y)
∴ the equation f (xy) = f (x) + f (y) holds.
Question 8. Write the following relations as sets of ordered pairs and find which of them are functions:
(i) {(x, y): y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
(ii) {(x, y): y > x + 1, x = 1, 2 and y = 2, 4, 6}
(iii) {(x, y): x + y = 3, x, y ∈ {0, 1, 2, 3}}
Solution:
(i) {(x, y): y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
When x = 1, y = 3(1) = 3
When x = 2, y = 3(2) = 6
When x = 3, y = 3(3) = 9
∴ R = {(1, 3), (2, 6), (3, 9)}
Hence, the given relation R is a function.
(ii) {(x, y): y > x + 1, x = 1, 2 and y = 2, 4, 6}
When x = 1, y > 1 + 1 or y > 2 ⇒ y = {4, 6}
When x = 2, y > 2 + 1 or y > 3 ⇒ y = {4, 6}
∴ R = {(1, 4), (1, 6), (2, 4), (2, 6)}
Hence, the given relation R is not a function.
(iii) {(x, y): x + y = 3, x, y ∈ {0, 1, 2, 3}}
When x = 0, 0 + y = 3 ⇒ y = 3
When x = 1, 1 + y = 3 ⇒ y = 2
When x = 2, 2 + y = 3 ⇒ y = 1
When x = 3, 3 + y = 3 ⇒ y = 0
∴ R = {(0, 3), (1, 2), (2, 1), (3, 0)}
Hence, the given relation R is a function.
Question 9. Let f: R → R and g: C → C be two functions defined as f(x) = x2 and g(x) = x2. Are they equal functions?
Solution:
Given:
f: R → R ∈ f(x) = x2 and g : R → R ∈ g(x) = x2
f is defined from R to R, the domain of f = R.
g is defined from C to C, the domain of g = C.
Two functions are equal only when the domain and codomain of both the functions are equal.
In this case, the domain of f ≠ domain of g.
∴ f and g are not equal functions.
Share your thoughts in the comments
Please Login to comment...