Question 26. Find the intervals in which f(x) = log (1 + x) – x/(1 + x) is increasing or decreasing.
Solution:
We have,
f(x) = log (1 + x) – x/(1 + x)
On differentiating both sides with respect to x, we get
f'(x) = 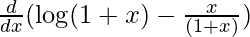
f'(x) = 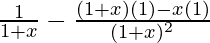
f'(x) = 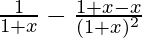
f'(x) = 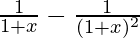
f'(x) = 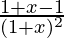
f'(x) = 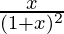
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 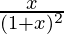 = 0
= 0
=> x = 0
Clearly, f'(x) > 0 if x > 0.
Also, f'(x) < 0 if –1 < x < 0 or x < –1.
Thus f(x) is increasing in (0, ∞) and decreasing in (–∞, –1) ∪ (–1, 0).
Question 27. Find the intervals in which f(x) = (x + 2)e–x is increasing or decreasing.
Solution:
We have,
f(x) = (x + 2)e–x
On differentiating both sides with respect to x, we get
f'(x) = 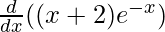
f'(x) = e–x – e–x (x + 2)
f'(x) = e–x (1 – x – 2)
f'(x) = e–x (x + 1)
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> e–x (x + 1) = 0
=> x = –1
Clearly, f'(x) > 0 if x < –1.
Also, f'(x) < 0 if x > –1.
Thus f(x) is increasing in (–∞, –1) and decreasing in (–1, ∞).
Question 28. Show that the function f given by f(x) = 10x is increasing for all x.
Solution:
We have,
f(x) = 10x
On differentiating both sides with respect to x, we get
f'(x) = 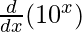
f'(x) = 10x log 10
Now we have, x ∈ R, we get
=> 10x > 0
=> 10x log 10 > 0
=> f'(x) > 0
Thus, f(x) is increasing for all x.
Hence proved.
Question 29. Prove that the function f given by f(x) = x – [x] is increasing in (0, 1).
Solution:
We have,
f(x) = x – [x]
On differentiating both sides with respect to x, we get
f'(x) = ![Rendered by QuickLaTeX.com \frac{d}{dx}(x - [x])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-60a73eca4975e25d39c798deba5b8cc9_l3.png)
f'(x) = 1
Now we have,
=> 1 > 0
=> f'(x) > 0
Thus, f(x) is increasing in the interval (0, 1).
Hence proved.
Question 30. Prove that the function f(x) = 3x5 + 40x3 + 240x is increasing on R.
Solution:
We have,
f(x) = 3x5 + 40x3 + 240x
On differentiating both sides with respect to x, we get
f'(x) = 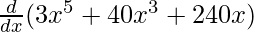
f'(x) = 15x4 + 120x2 + 240
f'(x) = 15 (x4 + 8x2 + 16)
f'(x) = 15 (x2 + 4)2
Now we know,
=> (x2 + 4)2 > 0
=> 15 (x2 + 4)2 > 0
=> f'(x) > 0
Thus, the given f(x) is increasing on R.
Hence proved.
Question 31. Prove that the function f given by f(x) = log cos x is strictly increasing on (–π/2, 0) and strictly decreasing on (0, π/2).
Solution:
We have,
f(x) = log cos x
On differentiating both sides with respect to x, we get
f'(x) = 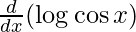
f'(x) = 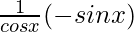
f'(x) = 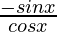
f'(x) = – tan x
Now for x ∈ (0, π/2), we get
=> 0 < x < π/2
=> tan 0 < tan x < tan π/2
=> 0 < tan x < 1
=> tan x > 0
=> – tan x < 0
=> f'(x) < 0
Also for x ∈ (–π/2, 0), we have,
=> –π/2 < x < 0
=> tan (–π/2) < tan x < tan 0
=> –1 < tan x < 0
=> tan x < 0
=> – tan x > 0
=> f'(x) > 0
Thus, f(x) is strictly increasing on the interval (–π/2, 0) and strictly decreasing on the interval (0, π/2).
Hence proved.
Question 32. Show that the function f given by f(x) = x3 – 3x2 + 4x is strictly increasing on R.
Solution:
We have,
f(x) = x3 – 3x2 + 4x
On differentiating both sides with respect to x, we get
f'(x) = 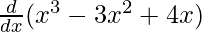
f'(x) = 3x2 – 6x + 4
f'(x) = 3 (x2 – 2x + 1) + 1
f'(x) = 3 (x – 1)2 + 1
Now, we know,
=> (x – 1)2 > 0
=> 3 (x – 1)2 > 0
=> 3 (x – 1)2 + 1 > 0
=> f'(x) > 0
Thus, f(x) is strictly increasing on R.
Hence proved.
Question 33. Show that the function f given by f(x) = cos x is strictly decreasing in (0, π), increasing in (π, 2π) and neither increasing or decreasing in (0, 2π).
Solution:
We have,
f(x) = cos x
On differentiating both sides with respect to x, we get
f'(x) = 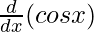
f'(x) = – sin x
Now for x ∈ (0, π), we get
=> 0 < x < π
=> sin 0 < sin x < sin π
=> 0 < sin x < 0
=> sin x > 0
=> – sin x < 0
=> f'(x) < 0
Also for x ∈ (π, 2π), we get
=> π < x < 2π
=> sin 0 < sin x < sin π
=> 0 < sin x < 0
=> sin x < 0
=> – sin x > 0
=> f'(x) > 0
Thus, f(x) is strictly increasing on the interval (π, 2π) and strictly decreasing on the interval (0, π).
So, the function is neither increasing or decreasing in (0, 2π).
Hence proved.
Question 34. Show that f(x) = x2 – x sin x is an increasing function on (0, π/2).
Solution:
We have,
f(x) = x2 – x sin x
On differentiating both sides with respect to x, we get
f'(x) = 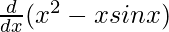
f'(x) = 2x – (x cos x + sin x)
f'(x) = 2x – x cos x – sin x
Now for x ∈ (0, π/2), we have
=> 0 ≤ sin x ≤ 1
=> 0 ≤ cos x ≤ 1
So, this implies,
=> 2x – x cos x – sin x > 0
=> f'(x) > 0
Thus, f(x) is an increasing function on the interval (0, π/2).
Hence proved.
Question 35. Find the value(s) of a for which f(x) = x3 – ax is an increasing function on R.
Solution:
We have,
f(x) = x3 – ax
On differentiating both sides with respect to x, we get
f'(x) = 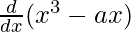
f'(x) = 3x2 – a
Now we are given that f(x) = x3 – ax is an increasing function on R, we get
=> f'(x) > 0
=> 3x2 – a > 0
=> a < 3x2
The critical point for 3x2 = 0 will be 0.
So, we get a ≤ 0.
Therefore, the values of a must be less than or equal to 0.
Question 36. Find the value of b for which the function f(x) = sin x – bx + c is a decreasing function on R.
Solution:
We have,
f(x) = sin x – bx + c
On differentiating both sides with respect to x, we get
f'(x) = 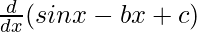
f'(x) = cos x – b + 0
f'(x) = cos x – b
Now we are given that f(x) = sin x – bx + c is a decreasing function on R, we get
=> f'(x) < 0
=> cos x – b < 0
=> b > cos x
The critical point for cos x = 0 will be 1.
So, we get b ≥ 1.
Therefore, the values of b must be greater than or equal to 1.
Question 37. Show that f(x) = x + cos x – a is an increasing function on R for all values of a.
Solution:
We have,
f(x) = x + cos x – a
On differentiating both sides with respect to x, we get
f'(x) = 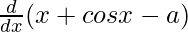
f'(x) = 1 – sin x
f'(x) = 
f'(x) = 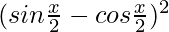
Now for x ∈ R, we have
=> 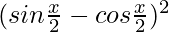 > 0
> 0
=> f'(x) > 0
Thus, the f(x) is an increasing function on R for all values of a.
Hence proved.
Question 38. Let f defined on [0, 1] be twice differentiable such that |f”(x)| ≤ 1 for all x ∈ [0, 1]. If f(0) = f(1), then show that f'(x) < 1 for all x ∈ [0, 1].
Solution:
As f(0) = f(1) and f is differentiable, we can apply Rolle’s theorem here. So, we get
f(c) = 0 for some c ∈ [0, 1].
On applying Lagrange’s mean value theorem, we get,
For point c and x ∈ [0, 1], so we have
=> 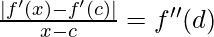
=> 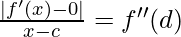
=> 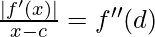
As we are given that |f”(d)| ≤ 1 for x ∈ [0, 1], we get
=> 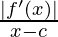 ≤ 1
≤ 1
=> |f'(x)| ≤ x – c
Now as both x and c lie in [0, 1], therefore x – c ∈ (0, 1).
This gives us, |f'(x)| < 1 for all x ∈ (0, 1).
Hence proved.
Question 39. Find the interval in which f(x) is increasing or decreasing:
(i) f(x) = x |x|, x ∈ R
Solution:
We have,
f(x) = x |x|, x ∈ R
=> 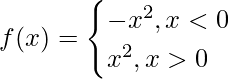
=> 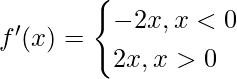
=> f'(x) > 0 for all values of x
Therefore, f(x) is an increasing function for all real values.
(ii) f(x) = sin x + |sin x|, 0 < x ≤ 2π
Solution:
We have,
f(x) = sin x + |sin x|, 0 < x ≤ 2π
=> 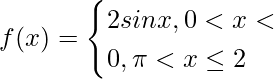
=> 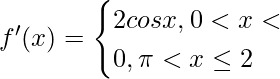
The function cos x is positive between the interval (0, π/2).
Therefore, the function is increasing in the interval (0, π/2).
Also, the function cos x is negative between the interval (π/2, π).
Therefore, the function is decreasing in the interval (0, π/2).
Now for π ≤ x ≤ 2π, value of f'(x) is 0.
Hence the function is neither increasing nor decreasing in the interval (π, 2π).
(iii) f(x) = sin x (1 + cos x), 0 < x ≤ π/2
Solution:
We have,
f(x) = sin x (1 + cos x)
On differentiating both sides with respect to x, we get
f'(x) = 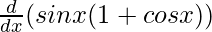
f'(x) = 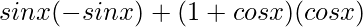
f'(x) = –sin2 x + cos x + cos2x
f'(x) = cos2 x – sin2 x + cos x
f'(x) = cos2 x – (1 – cos2 x) + cos x
f'(x) = cos2 x – 1 + cos2 x + cos x
f'(x) = 2 cos2 x + cos x – 1
f'(x) = 2 cos2 x + 2 cos x – cos x – 1
f'(x) = 2 cos x (cos x + 1) – 1 (cos x + 1)
f'(x) = (2 cos x – 1) (cos x + 1)
For f(x) to be increasing, we must have,
=> f'(x) > 0
=> (2 cos x – 1) (cos x + 1) > 0
=> 0 < x < π/3
=> x ∈ (0, π/3)
For f(x) to be decreasing, we must have,
=> f'(x) < 0
=> (2 cos x – 1) (cos x + 1) > 0
=> π/3 < x < π/2
=> x ∈ (π/3, π/2)
Thus, f(x) is increasing on the interval x ∈ (0, π/3) and decreasing on the interval x ∈ (π/3, π/2).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...