Class 11 RD Sharma Solutions – Chapter 19 Arithmetic Progressions- Exercise 19.4 | Set 2

Question 11. Find the sum of all integers between 100 and 550 which are divisible by 9.

Solution:

According to question

A.P = 108, 117…549 

From the given A.P. we get

a(first term) = 108, d(common difference) = 9, a_n(nth term) = 549 

Find the value of n using the given formula

a_n = a + (n – 1)d

549 = 108 + (n – 1)(9) 

441 = 9n – 9 

450 = 9n 

n = 50  

Now, we find the sum of the given A.P. using the following formula

S = n/2 [2a + (n -1)d]

S = 50/2 [2(108) + (50 – 1)(9)]

= 25 [216 + (49)(9)]

= 25 [216 + 441]

= 25 [657]

= 16425  

Hence,  the sum of all integers between 100 and 550 which are divisible by 9 = 16425

Question 12. Find the sum of the series:  

3 + 5 + 7 + 6 + 9 + 12 + 9 + 13 + 17 + … to 3n terms. 

Solution:

A.P = 3 +5 +7 + 9 + … to 3n  

From the given A.P. we get

a = 3, d = 2, n = 3n  

Now, we find the sum of the given A.P. using the following formula

S = n/2 [2a + (n – 1)d]

= 3n/2 [2(3) + (3n – 1)(2)]

= 3n [3 + (3n – 1)]

= 3n [3n + 2]

Hence, the sum of the given A.P = 3n [3n + 2]

Question 13. Find the sum of all those integers between 100 and 800 each of which on division by 16 leaves the remainder 7.

Solution:

According to question

A.P = 103, 119,…,791  

From the given A.P. we get

a = 103, l = 791  

Find the value of n using the given formula

a_n = a + (n – 1)d

791 = 103 + (n – 1)16 

n = 44

Now, we find the sum of the given A.P. using the following formula

S = n/2 [a + l]

S = 44/2 [103 + 791]

= 22 [894]

= 19668

Hence, the sum of all those integers between 100 and 800 

each of which on division by 16 leaves the remainder 7 = 19668

Question 14. Solve:  

(i) 25 + 22 + 19 + 16 + … + x = 115 

(ii) 1 +4+7+ 10 + … + x = 590

Solution:

(i) A.p= 25 + 22 + 19 + 16 +…+x = 115  

From the given A.P. we get

a = 25, d = -3, S = 115 

Using the formula

 S = n/2[2a + (n – 1)d] 

⇒ 115 = n/2 [2 x 25+ (n – 1)(-3)]

⇒ 115 x 2 = n[50 – 3n + 3] 

⇒ 230 = n(53 – 3n) 

⇒ 230 = 53n – 3n²

⇒ 3n² – 53n + 230 = 0 

Using quadratic formula: 

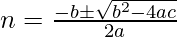
Now, Put the value of a = 3, b = – 53 and c = 230, we get

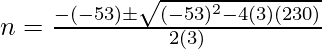
n = 46/6,10

⇒ n = 10 as n ≠ 46/6

So, a_n = x = a + (n – 1)d 

⇒ x = 25 + (10 – 1)(-3)

⇒ x = 25 – 27 = -2

Hence, the value of x = -2

(ii) A.P = 1 + 4 + 7 + 10 +….+ x = 590 

From the given A.P. we get

a = 1, d = 3  

Using the formula

S = n/2 [2a + (n – 1)d] 

⇒ 590 = n/2[2 x 1 + (n – 1)(3)] 

⇒ 590 x 2 = n[2 + 3n – 3] 

⇒ 1180 = n(3n – 1) 

⇒ 1180 = 3n² – n 

⇒ 3n² – n -1180 = 0 

Using quadratic formula: 

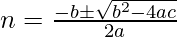
Now, Put the value of a = 3, b = – 1 and c = -1180, we get

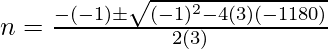
n = -118/6, 20

⇒ n = 20, as n ≠ -118/6 

a_n = x = a + (n – 1)d 

⇒ x = 1 + (20 – 1)(3) 

⇒ x = 1 + 60 – 3 = 58  

Hence, the value of x = 58

Question 15. Find the r^th term of an A.P., the sum of whose first n terms is 3n² + 2n. 

Solution:

According to the question

As, S_n = 3n² + 2n 

So, a = S₁ = 3 x 1² + 2 x 1 = 3 + 2 = 5 and 

S₂ = 3 x 2²+2 x 2 = 12+4 = 16 

⇒ a + a2 = 16 

⇒ a + a + d = 16 

⇒ 2a + d = 16 

⇒ 2 x 5 + d = 16 

⇒ d = 16 – 10 

⇒ d = 6 

Now, 

a_r = a + (r – 1)d 

= 5+ (r -1) x 6 

= 5 + 6r – 6

Hence, the a_r = 6r – 1

Question 16. How many terms are there in the A.P. whose first and fifth terms are -14 and 2 respectively and the sum of the terms is 40? 

Solution:

According to question we have

a = -14 and S_n = 40 ………………………. (i)

a₅ = 2 

By using formula

⇒ a + (5 – 1)d = 2 

⇒ -14 + 4d = 2 

⇒ 4d = 16 

⇒ d = 4  …………………………..(ii) 

By using formula

S_n = n/2 [2a + (n – 1)d] 

⇒ 40 = n/2 [2(-14) + (n – 1) x 4]                   ( From eq(i) and (ii)) 

⇒ 80 = n[-28 + 4n – 4] 

⇒ 80 = 4n² – 32n 

⇒ n² – 8n – 20 = 0 

⇒ (n -10)(n + 2) = 0 

⇒ n = 10, -2  

But n cannot be negative.

Hence, the total number of terms in the A.P = 10

Question 17. The sum of the first 7 terms of an A.P. is 10 and that of the next 7 terms is 17. Find the progression. 

Solution: 

According to question we have

S₇ = 10 

By using formula 

S_n = n/2 [2a + (n – 1)d] 

⇒ 7/2 [2a + (7 – 1)d] = 10 

⇒ 7/2 [2a + 6d] = 10  

⇒ a + 3d = 10/7   ………………………………… (i)

 Also, the sum of the next seven terms = S₁₄ – S₇ = 17 

⇒ 14/2 [2a + (14 – 1)d] – 7/2 [2a + (7 – 1)d] = 17 

⇒ 7[2a + 13d] – 7/2[2a + 6d] = 17  

14a + 91d – 7a – 21d = 17  

7a + 70d = 17  

a + 10d = 17/7  ………………………………….. (ii) 

From eq(i) and (ii), we get:

10/7 – 3d = 17/7 – 10d 

⇒ 7d = 1 

⇒ d = 1/7  

On putting the value in eq(i), we get:

 a + 3d = 10/7

⇒ a+ 3/7 = 10/7

⇒ a = 1, d = 1/7 

Hence, the progression = 1, 8/7, 9/7, 10/7 …

Question 18. The third term of an A.P. is 7 and the seventh term exceeds three times the third term by 2. Find the first term, the common difference, and the sum of first 20 terms. 

Solution:

According to question we have

a₃ = 7, a₇ – 3a₃ = 2  

By using formula 

a_n = a + (n – 1)d

⇒ a + (3 – 1)d = 7 

⇒ a + 2d = 7  …………………………………… (i) 

Also, 

a₇ – 3a₃ = 2 

⇒ a₇ – 21 = 2(Given) 

⇒ a + (7 – 1)d = 23 

⇒ a + 6d = 23 ………………………………………. (ii) 

From eq(i) and (ii), we get

4d = 16  

⇒ d = 4 

On putting the value in eq(i), we get   

a + 2(4) = 7

a = -1 

By using formula

S_n = n/2 [2a + (n – 1)d] 

S₂₀ = 20/2 [2(-1) + (20-1)(4)]

⇒ S₂₀ = 10[-2 + 76]

⇒ S₂₀ = 10[74] = 740

Hence, 

a = -1, d = 4, S₂₀ = 740

Question 19. The first term of an A.P. is 2 and the last term is 50. The sum of all these terms is 442. Find the common difference. 

Solution:

According to question we have

a = 2,l = 50, S_n = 442 

Now, S_n = 442 

⇒ n/2[a + l] = 442 

⇒ n/2 [2 + 50] = 442 

⇒ n = 17 

a₁₇ = 50 

By using formula, we get

⇒ a + (17 – 1) d = 50 

⇒ 2 + 16d = 50  

⇒ d = 3  

Question 20. The number of terms of an A.P. is even; the sum of odd terms is 24, of the even terms is 30, and the last term exceeds the first by 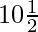, find the number of terms and the series.  

Solution:

According to question, we have

a₁ + a₃+… +a_2n-1 = 24 ……………..(1)  

a₂ + a₄+… +a_2n = 30 ……………..(2)  

Now, subtracting eq(1) from (2), we get: 

(d + d+…+ upto n terms) = 6 

⇒ nd = 6 ………….(3) 

Given : 

a_2n = a₁ + 21/2

⇒ a_2n – a₁ = 21/2

⇒ a + (2n – 1)d – a = 21/2  [a_2n= a + (2n – 1)d, a₁ = a]

⇒ 2nd – d = 21/2

⇒ 2 x 6 – d = 21/2 (From eq(3))  

⇒ d = 3/2 

On putting the value in eq(3), we get

n = 4 

⇒ 2n = 8 

Thus, there are 8 terms in the progression. 

To find the value of the first term: 

a₂ + a₄+…+a_2n = 30 

⇒ (a + d) + (a + 3d)+… +[a + (2n – 1)d] = 30 

⇒ n/2 [(a + d) + a + (2n – 1)d] = 30 

On putting n = 4 and d = 3/2, we get

a = 3/2

Hence, the series will be 1, 1/2, 3,  …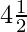

Question 21. If S_n = n²p and S_m = m² p, m ≠ n, in an A.P., prove that S_p = p³. 

Solution:

S_n = n²p

⇒ n/2 [2a + (n – 1)d] = n²p

⇒ 2np = 2a + (n – 1)d          ………………. (i) 

S_m = m²p

⇒ n/2 [2a + (m – 1)d] = m²p

⇒ 2mp = 2a + (m – 1)d       ……………….. (ii) 

On subtracting eq(ii) from eq(i), we get 

2p(n – m) = (n – m)d

2p = d                                ………………..(iii)

On substituting the value in eq(i), we get 

nd = 2a + (n – 1)d

⇒ nd – nd + d = 2a

⇒ a = d/2 = p [from eq(iii)]  ……………….(iv)

S_p = p/2[2a + (p – 1)d]

⇒ S_p = p/2[2p + (p – 1)2p]

⇒ S_p = p/2[2p + 2p² -2p]

⇒ S_p = p/2[2p²]

⇒ S_p = p³

Hence Proved

Question 22. If 12th term of an A.P. is -13 and the sum of the first four terms is 24, what is the sum of first 10 terms? 

Solution:

Let us considered first term = a and common difference = d

Given that a₁₂ = -13 

Using the formula

⇒ a + (12 – 1)d = -13 

⇒ a + 11d = -13           ………………. (i) 

Also, S₄ = 24 (given)

Using the formula

⇒ 4/2 [2a + (4 – 1)d] = 24 

⇒ 2(2a + 3d) = 24 

⇒ 2a + 3d = 12           ………………. (ii) 

From eq(i) and (ii), we get 

19d = -38 

d = -2 

Now put the value of d in eq(i), we get 

a + 11(-2) = -13  

⇒ a = 9 

S₁₀ = 10/2 [(2)(9) + (10 – 1)(-2)]

⇒ S₁₀ = 5[18 – 18] = 0

Hence, the sum of first ten terms = 0