Question 1. Find the intervals in which the following functions are increasing or decreasing.
(i) f(x) = 10 – 6x – 2x2
Solution:
We are given,
f(x) = 10 – 6x – 2x2
On differentiating both sides with respect to x, we get
f'(x) = 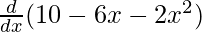
f'(x) = 0 – 6 – 4x
f'(x) = – 6 – 4x
For f(x) to be increasing, we must have,
=> f'(x) > 0
=> – 6 – 4x > 0
=> – 4x > 6
=> x < –6/4
=> x < –3/2
=> x ∈ (–∞, –3/2)
For f(x) to be decreasing, we must have,
=> f'(x) < 0
=> – 6 – 4x < 0
=> – 4x < 6
=> x > –6/4
=> x > –3/2
=> x ∈ ( –3/2, ∞)
Thus, f(x) is increasing on the interval x ∈ (–∞, –3/2) and decreasing on the interval x ∈ ( –3/2, ∞).
(ii) f(x) = x2 + 2x – 5
Solution:
We are given,
f(x) = x2 + 2x – 5
On differentiating both sides with respect to x, we get
f'(x) = 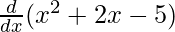
f'(x) = 2x + 2 – 0
f'(x) = 2x + 2
For f(x) to be increasing, we must have,
=> f'(x) > 0
=> 2x + 2 > 0
=> 2x > –2
=> x > –2/2
=> x > –1
=> x ∈ (–1, ∞)
For f(x) to be decreasing, we must have,
=> f'(x) < 0
=> 2x + 2 < 0
=> 2x < –2
=> x < –2/2
=> x < –1
=> x ∈ (–∞, –1)
Thus, f(x) is increasing on the interval x ∈ (–1, ∞) and decreasing on the interval x ∈ ( –∞, –1).
(iii) f(x) = 6 – 9x – x2
Solution:
We are given,
f(x) = 6 – 9x – x2
On differentiating both sides with respect to x, we get
f'(x) = 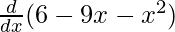
f'(x) = 0 – 9 – 2x
f'(x) = – 9 – 2x
For f(x) to be increasing, we must have,
=> f'(x) > 0
=> –9 – 2x > 0
=> –2x > 9
=> x > –9/2
=> x ∈ (–9/2, ∞)
For f(x) to be decreasing, we must have,
=> f'(x) < 0
=> –9 – 2x < 0
=> –2x < 9
=> x < –9/2
=> x ∈ (–∞, –9/2)
Thus, f(x) is increasing on the interval x ∈ (–9/2, ∞) and decreasing on the interval x ∈ ( –∞, –9/2).
(iv) f(x) = 2x3 – 12x2 + 18x + 15
Solution:
We are given,
f(x) = 2x3 – 12x2 + 18x + 15
On differentiating both sides with respect to x, we get
f'(x) = 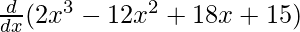
f'(x) = 6x2 – 24x + 18 + 0
f'(x) = 6x2 – 24x + 18
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 6x2 – 24x + 18 = 0
=> 6 (x2 – 4x + 3) = 0
=> x2 – 4x + 3 = 0
=> x2 – 3x – x + 3 = 0
=> x (x – 3) – 1 (x – 3) = 0
=> (x – 1) (x – 3) = 0
=> x = 1, 3
Clearly, f'(x) > 0 if x < 1 and x > 3.
Also, f'(x) < 0, if 1 < x < 3.
Thus, f(x) is increasing on the interval x ∈ (–∞, 1)∪ (3, ∞) and decreasing on the interval x ∈ (1, 3).
(v) f(x) = 5 + 36x + 3x2 – 2x3
Solution:
We are given,
f(x) = 5 + 36x + 3x2 – 2x3
On differentiating both sides with respect to x, we get
f'(x) = 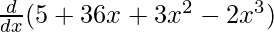
f'(x) = 0 + 36 + 6x – 6x2
f'(x) = 36 + 6x – 6x2
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 36 + 6x – 6x2 = 0
=> 6 (– x2 + x + 6) = 0
=> 6 (–x2 + 3x – 2x + 6) = 0
=> –x2 + 3x – 2x + 6 = 0
=> x2 – 3x + 2x – 6 = 0
=> (x – 3) (x + 2) = 0
=> x = 3, – 2
Clearly, f’(x) > 0 if –2 < x < 3.
Also f’(x) < 0 if x < –2 and x > 3.
Thus, f(x) is increasing on x ∈ (–2, 3) and f(x) is decreasing on interval x ∈ (–∞, –2) ∪ (3, ∞).
(vi) f(x) = 8 + 36x + 3x2 – 2x3
Solution:
We are given,
f(x) = 8 + 36x + 3x2 – 2x3
On differentiating both sides with respect to x, we get
f'(x) = 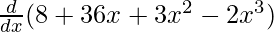
f'(x) = 0 + 36 + 6x – 6x2
f'(x) = 36 + 6x – 6x2
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 36 + 6x – 6x2 = 0
=> 6 (– x2 + x + 6) = 0
=> 6 (–x2 + 3x – 2x + 6) = 0
=> –x2 + 3x – 2x + 6 = 0
=> x2 – 3x + 2x – 6 = 0
=> (x – 3) (x + 2) = 0
=> x = 3, –2
Clearly, f’(x) > 0 if –2 < x < 3.
Also f’(x) < 0 if x < –2 and x > 3.
Thus, f(x) is increasing on x ∈ (–2, 3) and f(x) is decreasing on interval x ∈ (–∞, –2) ∪ (3, ∞).
(vii) f(x) = 5x3 – 15x2 – 120x + 3
Solution:
We are given,
f(x) = 5x3 – 15x2 – 120x + 3
On differentiating both sides with respect to x, we get
f'(x) = 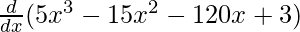
f'(x) = 15x2 – 30x – 120 + 0
f'(x) = 15x2 – 30x – 120
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 15x2 – 30x – 120 = 0
=> 15(x2 – 2x – 8) = 0
=> 15(x2 – 4x + 2x – 8) = 0
=> x2 – 4x + 2x – 8 = 0
=> (x – 4) (x + 2) = 0
=> x = 4, –2
Clearly, f’(x) > 0 if x < –2 and x > 4.
Also f’(x) < 0 if –2 < x < 4.
Thus, f(x) is increasing on x ∈ (–∞,–2) ∪ (4, ∞) and f(x) is decreasing on interval x ∈ (–2, 4).
(viii) f(x) = x3 – 6x2 – 36x + 2
Solution:
We are given,
f(x) = x3 – 6x2 – 36x + 2
On differentiating both sides with respect to x, we get
f'(x) = 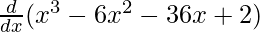
f'(x) = 3x2 – 12x – 36 + 0
f'(x) = 3x2 – 12x – 36
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 3x2 – 12x – 36 = 0
=> 3(x2 – 4x – 12) = 0
=> 3(x2 – 6x + 2x – 12) = 0
=> x2 – 6x + 2x – 12 = 0
=> (x – 6) (x + 2) = 0
=> x = 6, –2
Clearly, f’(x) > 0 if x < –2 and x > 6.
Also f’(x) < 0 if –2< x < 6
Thus, f(x) is increasing on x ∈ (–∞,–2) ∪ (6, ∞) and f(x) is decreasing on interval x ∈ (–2, 6).
(ix) f(x) = 2x3 – 15x2 + 36x + 1
Solution:
We are given,
f(x) = 2x3 – 15x2 + 36x + 1
On differentiating both sides with respect to x, we get
f'(x) = 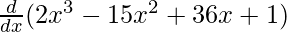
f'(x) = 6x2 – 30x + 36 + 0
f'(x) = 6x2 – 30x + 36
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 6x2 – 30x + 36 = 0
=> 6 (x2 – 5x + 6) = 0
=> 6(x2 – 3x – 2x + 6) = 0
=> x2 – 3x – 2x + 6 = 0
=> (x – 3) (x – 2) = 0
=> x = 3, 2
Clearly, f’(x) > 0 if x < 2 and x > 3.
Also f’(x) < 0 if 2 < x < 3.
Thus, f(x) is increasing on x ∈ (–∞, 2) ∪ (3, ∞) and f(x) is decreasing on interval x ∈ (2, 3).
(x) f(x) = 2x3 + 9x2 + 12x + 1
Solution:
We are given,
f(x) = 2x3 + 9x2 + 12x + 1
On differentiating both sides with respect to x, we get
f'(x) = 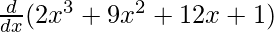
f'(x) = 6x2 + 18x + 12 + 0
f'(x) = 6x2 + 18x + 12
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 6x2 + 18x + 12 = 0
=> 6 (x2 + 3x + 2) = 0
=> 6(x2 + 2x + x + 2) = 0
=> x2 + 2x + x + 2 = 0
=> (x + 2) (x + 1) = 0
=> x = –1, –2
Clearly, f’(x) > 0 if –2 < x < –1.
Also f’(x) < 0 if x < –1 and x > –2.
Thus, f(x) is increasing on x ∈ (–2,–1) and f(x) is decreasing on interval x ∈ (–∞, –2) ∪ (–2, ∞).
(xi) f(x) = 2x3 – 9x2 + 12x – 5
Solution:
We are given,
f(x) = 2x3 – 9x2 + 12x – 5
On differentiating both sides with respect to x, we get
f'(x) = 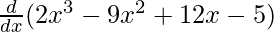
f'(x) = 6x2 – 18x + 12 – 0
f'(x) = 6x2 – 18x + 12
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 6x2 – 18x + 12 = 0
=> 6 (x2 – 3x + 2) = 0
=> 6(x2 – 2x – x + 2) = 0
=> x2 – 2x – x + 2 = 0
=> (x – 2) (x – 1) = 0
=> x = 1, 2
Clearly, f’(x) > 0 if x < 1 and x > 2.
Also f’(x) < 0 if 1 < x < 2.
Thus, f(x) is increasing on x ∈ (–∞, 1) ∪ (2, ∞) and f(x) is decreasing on interval x ∈ (1, 2).
(xii) f(x) = 6 + 12x + 3x2 – 2x3
Solution:
We are given,
f(x) = 6 + 12x + 3x2 – 2x3
On differentiating both sides with respect to x, we get
f'(x) = 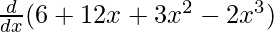
f'(x) = 0 + 12 + 6x – 6x2
f'(x) = 12 + 6x – 6x2
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 12 + 6x – 6x2 = 0
=> 6 (–x2 + x + 2) = 0
=> x2 – x – 2 = 0
=> x2 – 2x + x – 2 = 0
=> (x – 2) (x + 1) = 0
=> x = 2, –1
Clearly, f’(x) > 0 if –1 < x < 2.
Also f’(x) < 0 if x < –1 and x > 2.
Thus, f(x) is increasing on x ∈ (–1, 2) and f(x) is decreasing on interval x ∈ (–∞, –1) ∪ (2, ∞).
(xiii) f(x) = 2x3 – 24x + 107
Solution:
We are given,
f(x) = 2x3 – 24x + 107
On differentiating both sides with respect to x, we get
f'(x) = 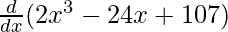
f'(x) = 6x2 – 24 + 0
f'(x) = 6x2 – 24
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 6x2 – 24 = 0
=> 6x2 = 24
=> x2 = 4
=> x = 2, –2
Clearly, f’(x) > 0 if x < –2 and x > 2.
Also f’(x) < 0 if –2 < x < 2.
Thus, f(x) is increasing on x ∈ (–∞, –2) ∪ (2, ∞), and f(x) is decreasing on interval x ∈ (–2, 2).
(xiv) f(x) = –2x3 – 9x2 – 12x + 1
Solution:
We are given,
f(x) = –2x3 – 9x2 – 12x + 1
On differentiating both sides with respect to x, we get
f'(x) = 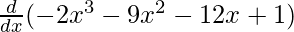
f'(x) = –6x2 – 18x – 12 + 0
f'(x) = –6x2 – 18x – 12
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> –6x2 – 18x – 12 = 0
=> 6 (–x2 – 3x – 2) = 0
=> x2 + 3x + 2 = 0
=> x2 + 2x + x + 2 = 0
=> (x + 2) (x + 1) = 0
=> x = –2, –1
Clearly, f’(x) > 0 if x < –1 and x > –2.
Also, f’(x) < 0 if –2 < x < –1.
Thus, f(x) is increasing on x ∈ (–2, –1) and f(x) is decreasing on interval x ∈ (–∞, –2) ∪ (–1, ∞).
(xv) f(x) = (x – 1) (x – 2)2
Solution:
We are given,
f(x) = (x – 1) (x – 2)2
On differentiating both sides with respect to x, we get
f'(x) = 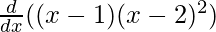
f'(x) = (x – 2)2 + 2 (x – 1) (x – 2)
f'(x) = (x – 2) (x – 2 + 2x – 2)
f'(x) = (x – 2) (3x – 4)
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> (x – 2) (3x – 4) = 0
=> x = 2, 4/3
Clearly, f’(x) > 0 if x < 4/3 and x > 2.
Also, f’(x) < 0 if 4/3 < x < 2.
Thus, f(x) is increasing on x ∈ (–∞, 4/3) ∪ (2, ∞) and f(x) is decreasing on interval x ∈ (4/3, 2).
(xvi) f(x) = x3 – 12x2 + 36x + 17
Solution:
We are given,
f(x) = x3 – 12x2 + 36x + 17
On differentiating both sides with respect to x, we get
f'(x) = 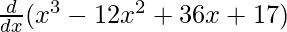
f'(x) = 3x2 – 24x + 36 + 0
f'(x) = 3x2 – 24x + 36
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 3x2 – 24x + 36 = 0
=> 3 (x2 – 8x + 12) = 0
=> x2 – 8x + 12 = 0
=> x2 – 6x – 2x + 12 = 0
=> (x – 6) (x – 2) = 0
=> x = 6, 2
Clearly, f’(x) > 0 if x < 2 and x > 6.
Also, f’(x) < 0 if 2 < x < 6.
Thus, f(x) is increasing on x ∈ (–∞, 2) ∪ (6, ∞) and f(x) is decreasing on interval x ∈ (2, 6).
(xvii) f(x) = 2x3 – 24x + 7
Solution:
We are given,
f(x) = 2x3 – 24x + 7
On differentiating both sides with respect to x, we get
f'(x) = 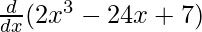
f'(x) = 6x2 – 24 + 0
f'(x) = 6x2 – 24
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 6x2 – 24 = 0
=> 6x2 = 24
=> x2 = 4
=> x = 2, –2
Clearly, f’(x) > 0 if x < –2 and x > 2.
Also f’(x) < 0 if –2 < x < 2.
Thus, f(x) is increasing on x ∈ (–∞, –2) ∪ (2, ∞), and f(x) is decreasing on interval x ∈ (–2, 2).
(xviii) f(x) = 3x4/10 – 4x3/5 -3x2 + 36x/5 + 11
Solution:
We are given,
f(x) = 3x4/10 – 4x3/5 -3x2 + 36x/5 + 11
On differentiating both sides with respect to x, we get
f'(x) = 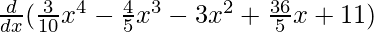
f'(x) = 6x3/5 – 12x2/5 -3(2x) + 36/5
f'(x) = 6/5[(x – 1)(x + 2)(x – 3)]
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 6/5[(x – 1)(x + 2)(x – 3)] = 0
=> x = 1, –2, 3
Clearly, f’(x) > 0 if –2 < x < 1 and if x > 3
Also f’(x) < 0 if 1 < x < 3.
Thus, f(x) is increasing on x ∈ (3, ∞) and f(x) is decreasing on interval x ∈ (1, 3).
(xix) f(x) = x4 – 4x
Solution:
We are given,
f(x) = x4 – 4x
On differentiating both sides with respect to x, we get
f'(x) = 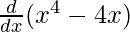
f'(x) = 4x3 – 4
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 4x3 – 4 = 0
=> 4 (x3 – 1) = 0
=> x3 – 1 = 0
=> x3 = 1
=> x = 1
Clearly, f’(x) > 0 if x > 1.
Also f’(x) < 0 if x < 1.
Thus, f(x) is increasing on x ∈ (1, ∞), and f(x) is decreasing on interval x ∈ (–∞, 1).
(xx) f(x) = x4/4 + 2/3x3 – 5/2x2 – 6x + 7
Solution:
We have,
f(x) = x4/4 + 2/3x3 – 5/2x2 – 6x + 7
On differentiating both sides with respect to x, we get
f'(x) = 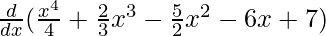
f'(x) = 4x3/4 + 6x2/3 – 10x/2 – 6 + 0
f'(x) = x3 + 2x2 – 5x – 6
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> x3 + 2x2 – 5x – 6 = 0
=> (x + 1) (x + 3) (x – 2) = 0
=> x = –1, –3, 2
Clearly f'(x) > 0 if –3 < x < –1 and x > 2.
Also f'(x) < 0 if x < –3 and –1 < x < 2.
Thus, f(x) is increasing on x ∈ (–3, –1) ∪ (2, ∞) and f(x) is decreasing on interval x ∈ (–∞, –3) ∪ (–1, 2).
(xxi) f(x) = x4 – 4x3 + 4x2 + 15
Solution:
We have,
f(x) = x4 – 4x3 + 4x2 + 15
On differentiating both sides with respect to x, we get
f'(x) = 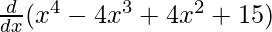
f'(x) = 4x3 – 12x2 + 8x + 0
f'(x) = 4x3 – 12x2 + 8x
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 4x3 – 12x2 + 8x = 0
=> 4x (x2 – 3x + 2) = 0
=> 4x (x – 2) (x – 1) = 0
=> x = 0, 1, 2
Clearly f'(x) > 0 if 0 < x < 1 and x > 2.
Also f'(x) < 0 if x < 0 and 1 < x < 2.
Thus, f(x) is increasing on x ∈ (0, 1) ∪ (2, ∞) and f(x) is decreasing on interval x ∈ (–∞, 0) ∪ (1, 2).
(xxii) f(x) = 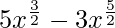 , x > 0
, x > 0
Solution:
We have,
f(x) = 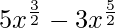
On differentiating both sides with respect to x, we get
f'(x) = 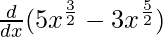
f'(x) = 
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=>  = 0
= 0
=> 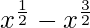 = 0
= 0
=> x1/2(1 – x) = 0
=> x = 0, 1
Clearly f'(x) > 0 if 0 < x < 1.
Also f'(x) < 0 if x > 0.
Thus, f(x) is increasing on x ∈ (0, 1) and f(x) is decreasing on interval x ∈ (1, ∞).
(xxiii) f(x) = x8 + 6x2
Solution:
We have,
f(x) = x8 + 6x2
On differentiating both sides with respect to x, we get
f'(x) = 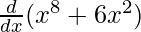
f'(x) = 8x7 + 12x
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 8x7 + 12x = 0
=> 4x (2x6 + 3) = 0
=> x = 0
Clearly f'(x) > 0 if x > 0.
Also f'(x) < 0 if x < 0.
Thus, f(x) is increasing on x ∈ (0, ∞) and f(x) is decreasing on interval x ∈ (–∞, 0).
(xxiv) f(x) = x3 – 6x2 + 9x + 15
Solution:
We are given,
f(x) = x3 – 6x2 + 9x + 15
On differentiating both sides with respect to x, we get
f'(x) = 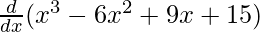
f'(x) = 3x2 – 12x + 9 + 0
f'(x) = 3x2 – 12x + 9
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 3x2 – 12x + 9 = 0
=> 3 (x2 – 4x + 3) = 0
=> x2 – 4x + 3 = 0
=> x2 – 3x – x + 3 = 0
=> (x – 3) (x – 1) = 0
=> x = 3, 1
Clearly f'(x) > 0 if x < 1 and x > 3.
Also f'(x) < 0 if 1 < x < 3.
Thus, f(x) is increasing on x ∈ (–∞, 1) ∪ (3, ∞) and f(x) is decreasing on interval x ∈ (1, 3).
(xxv) f(x) = [x(x – 2)]2
Solution:
We are given,
f(x) = [x(x – 2)]2
On differentiating both sides with respect to x, we get
f'(x) = ![Rendered by QuickLaTeX.com \frac{d}{dx}[x(x - 2)]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-01185a523de3e85ae9b921daf228a1f6_l3.png)
f'(x) = 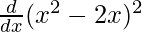
f'(x) = 2 (x2 – 2x) (2x – 2)
f'(x) = 4x (x – 2) (x – 1)
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 4x (x – 2) (x – 1) = 0
=> x = 0, 1, 2
Clearly f'(x) > 0 if 0 < x < 1 and x > 2.
Also f'(x) < 0 if x < 0 and 1< x < 2.
Thus, f(x) is increasing on x ∈ (0, 1) ∪ (2, ∞) and f(x) is decreasing on interval x ∈ (–∞, 0) ∪ (1, 2).
(xxvi) f(x) = 3x4 – 4x3 – 12x2 + 5
Solution:
We are given,
f(x) = 3x4 – 4x3 – 12x2 + 5
On differentiating both sides with respect to x, we get
f'(x) = 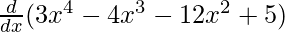
f'(x) = 12x3 – 12x2 – 24x
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 12x3 – 12x2 – 24x = 0
=> 12x (x2 – x – 2) = 0
=> 12x (x + 1) (x – 2) = 0
=> x = 0, –1, 2
Clearly f'(x) > 0 if –1 < x < 0 and x > 2.
Also f'(x) < 0 if x < –1 and 0< x < 2.
Thus, f(x) is increasing on x ∈ (–1, 0) ∪ (2, ∞) and f(x) is decreasing on interval x ∈ (–∞, –1) ∪ (0, 2).
(xxvii) f(x) = 3x4/2 – 4x3 – 45x2 + 51
Solution:
We have,
f(x) = 3x4/2 – 4x3 – 45x2 + 51
On differentiating both sides with respect to x, we get
f'(x) = 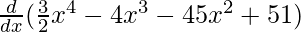
f'(x) = 6x3 – 12x2 – 90x
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> 6x3 – 12x2 – 90x = 0
=> 6x (x2 – 2x – 15) = 0
=> 6x (x + 3) (x – 5) = 0
=> x = 0, –3, 5
Clearly f'(x) > 0 if –3 < x < 0 and x > 5.
Also f'(x) < 0 if x < –3 and 0< x < 5.
Thus, f(x) is increasing on x ∈ (–3, 0) ∪ (5, ∞) and f(x) is decreasing on interval x ∈ (–∞, –3) ∪ (0, 5).
(xxvii) f(x) = 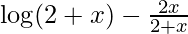
Solution:
We have,
f(x) = 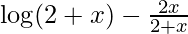
On differentiating both sides with respect to x, we get
f'(x) = 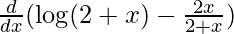
f'(x) = 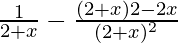
f'(x) = 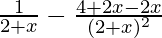
f'(x) = 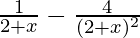
f'(x) = 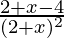
f'(x) = 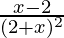
Clearly f'(x) > 0 if x > 2.
Also f'(x) < 0 if x < 2
Thus, f(x) is increasing on x ∈ (2, ∞) and f(x) is decreasing on interval x ∈ (–∞, 2).
Question 2. Determine the values of x for which the function f(x) = x2 – 6x + 9 is increasing or decreasing. Also, find the coordinates of the point on the curve y = x2 – 6x + 9 where the normal is parallel to the line y = x + 5.
Solution:
Given f(x) = x2 – 6x + 9
On differentiating both sides with respect to x, we get
=> f’(x) = 2x – 6
=> f’(x) = 2(x – 3)
For f(x), we need to find the critical point, so we get,
=> f’(x) = 0
=> 2(x – 3) = 0
=> (x – 3) = 0
=> x = 3
Clearly, f’(x) > 0 if x > 3.
Also f’(x) < 0 if x < 3.
Thus, f(x) is increasing on (3, ∞) and f(x) is decreasing on interval x ∈ (–∞, 3).
Equation of the given curve is f(x) = x2 – 6x + 9.
Slope of this curve is given by,
=> m1 = dy/dx
=> m1 = 2x – 6
And slope of the line is y = x + 5
Slope of this curve is given by,
=> m2 = dy/dx
=> m2 = 1
Now according to the question,
=> m1m2 = –1
=> 2x – 6 = –1
=> 2x = 5
=> x = 5/2
Putting x = 5/2 in the curve y = x2 – 6x + 9, we get,
=> y = (5/2)2 – 6 (5/2) + 9
=> y = 25/4 – 15 + 9
=> y = 1/4
Therefore, the required coordinates are (5/2, 1/4).
Question 3. Find the intervals in which f(x) = sin x – cos x, where 0 < x < 2π is increasing or decreasing.
Solution:
We have,
f(x) = sin x – cos x
On differentiating both sides with respect to x, we get
f'(x) = \frac{d}{dx}(sin x – cos x)
f'(x) = cos x + sin x
For f(x), we need to find the critical point, so we get,
=> f'(x) = 0
=> cos x + sin x = 0
=> 1 + tan x = 0
=> tan x = –1
=> x = 3π/4 , 7π/4
Clearly f'(x) > 0 if 0 < x < 3π/4 and 7π/4 < x < 2π.
Also f'(x) < 0 if 3π/4 < x < 7π/4.
Thus, f(x) is increasing on x ∈ (0, 3π/4) ∪ (7π/4, 2π) and f(x) is decreasing on interval x ∈ (3π/4, 7π/4).
Question 4. Show that f(x) = e2x is increasing on R.
Solution:
We have,
=> f(x) = e2x
On differentiating both sides with respect to x, we get
f'(x) = 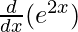
f'(x) = 2e2x
For f(x) to be increasing, we must have
=> f’(x) > 0
=> 2e2x > 0
=> e2x > 0
Now we know, the value of e lies between 2 and 3. Therefore, f(x) will be always greater than zero.
Thus, f(x) is increasing on interval R.
Hence proved.
Question 5. Show that f(x) = e1/x, x ≠ 0 is a decreasing function for all x ≠ 0.
Solution:
We have,
=> f(x) = e1/x
On differentiating both sides with respect to x, we get
f'(x) = 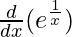
f'(x) = -ex/x2
As x ∈ R, we have,
=> ex > 0
Also, we get,
=> 1/x2 > 0
This means, ex/x2 > 0
=> -ex/x2 < 0
Thus, f(x) is a decreasing function for all x ≠ 0.
Hence proved.
Question 6. Show that f(x) = loga x, 0 < a < 1 is a decreasing function for all x > 0.
Solution:
We have,
=> f(x) = loga x
On differentiating both sides with respect to x, we get
f'(x) = 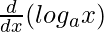
f'(x) = 1/xloga
As we are given 0 < a < 1,
=> log a < 0
And for x > 0, 1/x > 0
Therefore, f'(x) is,
=> 1/xloga < 0
=> f'(x) < 0
Thus, f(x) is a decreasing function for all x > 0.
Hence proved.
Question 7. Show that f(x) = sin x is increasing on (0, π/2) and decreasing on (π/2, π) and neither increasing nor decreasing in (0, π).
Solution:
We have,
f(x) = sin x
On differentiating both sides with respect to x, we get
f'(x) = 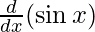
f'(x) = cos x
Now for 0 < x < π/2,
=> cos x > 0
=> f'(x) > 0
And for π/2 < x < π,
=> cos x < 0
=> f'(x) < 0
Thus, f(x) is increasing on x ∈ (0, π/2) and f(x) is decreasing on interval x ∈ (π/2, π).
Hence f(x) is neither increasing nor decreasing in (0, π).
Hence proved.
Question 8. Show that f(x) = log sin x is increasing on (0, π/2) and decreasing on (π/2, π).
Solution:
We have,
f(x) = log sin x
On differentiating both sides with respect to x, we get
f'(x) = 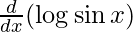
f'(x) = (1/sinx)cosx
f'(x) = cot x
Now for 0 < x < π/2,
=> cot x > 0
=> f'(x) > 0
And for π/2 < x < π,
=> cos x < 0
=> f'(x) < 0
Thus, f(x) is increasing on x ∈ (0, π/2) and f(x) is decreasing on interval x ∈ (π/2, π).
Hence proved.
Question 9. Show that f(x) = x – sin x is increasing for all x ∈ R.
Solution:
We have,
f(x) = x – sin x
On differentiating both sides with respect to x, we get
f'(x) = 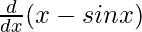
f'(x) = 1 – cos x
Now, we are given x ∈ R, we get
=> –1 < cos x < 1
=> –1 > cos x > 0
=> f’(x) > 0
Thus, f(x) is increasing on interval x ∈ R.
Hence proved.
Question 10. Show that f(x) = x3 – 15x2 + 75x – 50 is an increasing function for all x ∈ R.
Solution:
We have,
f(x) = x3 – 15x2 + 75x – 50
On differentiating both sides with respect to x, we get
f'(x) = 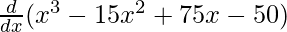
f'(x) = 3x2 – 30x + 75 – 0
f'(x) = 3x2 – 30x + 75
f’(x) = 3(x2 – 10x + 25)
f’(x) = 3(x – 5)2
Now, as we are given x ϵ R, we get
=> (x – 5)2 > 0
=> 3(x – 5)2 > 0
=> f’(x) > 0
Thus, f(x) is increasing on interval x ∈ R.
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...