Class 12 RD Sharma Solutions – Chapter 17 Increasing and Decreasing Functions – Exercise 17.2 | Set 2
Last Updated :
15 Feb, 2022
Question 11. Show that f(x) = cos2 x is a decreasing function on (0, π/2).
Solution:
We have,
f(x) = cos2 x
On differentiating both sides with respect to x, we get
f'(x) = 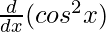
f'(x) = 2 cos x (– sin x)
f'(x) = – sin 2x
Now for 0 < x < π/2,
=> sin 2x > 0
=> – sin 2x < 0
=> f'(x) < 0
Thus, f(x) is decreasing on x ∈ (0, π/2).
Hence proved.
Question 12. Show that f(x) = sin x is an increasing function on (–π/2, π/2).
Solution:
We have,
f(x) = sin x
On differentiating both sides with respect to x, we get
f'(x) = 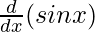
f'(x) = cos x
Now for –π/2 < x < π/2,
=> cos x > 0
=> f'(x) > 0
Thus, f(x) is increasing on x ∈ (–π/2, π/2).
Hence proved.
Question 13. Show that f(x) = cos x is a decreasing function on (0, π), increasing in (–π, 0) and neither increasing nor decreasing in (–π, π).
Solution:
We have,
f(x) = cos x
On differentiating both sides with respect to x, we get
f'(x) = 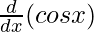
f'(x) = – sin x
Now for 0 < x < π,
=> sin x > 0
=> – sin x < 0
=> f’(x) < 0
And for –π < x < 0,
=> sin x < 0
=> – sin x > 0
=> f’(x) > 0
Therefore, f(x) is decreasing in (0, π) and increasing in (–π, 0).
Hence f(x) is neither increasing nor decreasing in (–π, π).
Hence proved.
Question 14. Show that f(x) = tan x is an increasing function on (–π/2, π/2).
Solution:
We have,
f(x) = tan x
On differentiating both sides with respect to x, we get
f'(x) = 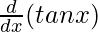
f'(x) = sec2 x
Now for –π/2 < x < π/2,
=> sec2 x > 0
=> f’(x) > 0
Thus, f(x) is increasing on interval (–π/2, π/2).
Hence proved.
Question 15. Show that f(x) = tan–1 (sin x + cos x) is a decreasing function on the interval (π/4, π /2).
Solution:
We have,
f(x) = tan–1 (sin x + cos x)
On differentiating both sides with respect to x, we get
f'(x) = 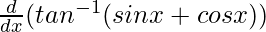
f'(x) = 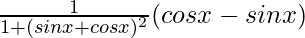
f'(x) = 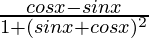
f'(x) = 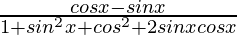
f'(x) = 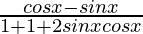
f'(x) = 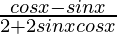
f'(x) = 
Now for π/4 < x < π/2,
=> 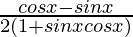 < 0
< 0
=> f’(x) < 0
Thus, f(x) is decreasing on interval (π/4, π/2).
Hence proved.
Question 16. Show that the function f(x) = sin (2x + π/4) is decreasing on (3π/8, 5π/8).
Solution:
We have,
f(x) = sin (2x + π/4)
On differentiating both sides with respect to x, we get
f'(x) = 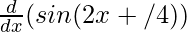
f'(x) = 2 cos (2x + π/4)
Now we have, 3π/8 < x < 5π/8
=> 3π/4 < 2x < 5π/4
=> 3π/4 + π/4 < 2x + π/4 < 5π/4 + π/4
=> π < 2x + π/4 + 3π/2
As, 2x + π/4 lies in 3rd quadrant, we get,
=> cos (2x + π/4) < 0
=> 2 cos (2x + π/4) < 0
=> f'(x) < 0
Thus, f(x) is decreasing on interval (3π/8, 5π/8).
Hence proved.
Question 17. Show that the function f(x) = cot–1 (sin x + cos x) is increasing on (0, π/4) and decreasing on (π/4, π/2).
Solution:
We have,
f(x) = cot–1 (sin x + cos x)
On differentiating both sides with respect to x, we get
f'(x) = 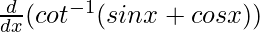
f'(x) = 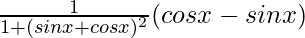
f'(x) = 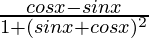
f'(x) = 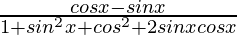
f'(x) = 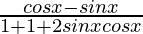
f'(x) = 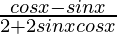
f'(x) = 
Now for π/4 < x < π/2,
=> 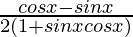 < 0
< 0
=> cos x – sin x < 0
=> f’(x) < 0
Also for 0 < x < π/4,
=> 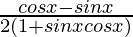 > 0
> 0
=> cos x – sin x > 0
=> f'(x) > 0
Thus, f(x) is increasing on interval (0, π/4) and decreasing on intervals (π/4, π/2).
Hence proved.
Question 18. Show that f(x) = (x – 1) ex + 1 is an increasing function for all x > 0.
Solution:
We have,
f(x) = (x – 1) ex + 1
On differentiating both sides with respect to x, we get
f'(x) = 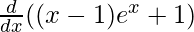
f'(x) = ex + (x – 1) ex
f'(x) = ex(1+ x – 1)
f'(x) = x ex
Now for x > 0,
⇒ ex > 0
⇒ x ex > 0
⇒ f’(x) > 0
Thus f(x) is increasing on interval x > 0.
Hence proved.
Question 19. Show that the function x2 – x + 1 is neither increasing nor decreasing on (0, 1).
Solution:
We have,
f(x) = x2 – x + 1
On differentiating both sides with respect to x, we get
f'(x) = 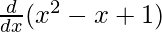
f'(x) = 2x – 1 + 0
f'(x) = 2x – 1
Now for 0 < x < 1/2, we have
=> 2x – 1 < 0
=> f(x) < 0
Also for 1/2 < x < 1,
=> 2x – 1 > 0
=> f(x) > 0
Thus f(x) is increasing on interval (1/2, 1) and decreasing on interval (0, 1/2).
Hence, the function is neither increasing nor decreasing on (0, 1).
Hence proved.
Question 20. Show that f(x) = x9 + 4x7 + 11 is an increasing function for all x ∈ R.
Solution:
We have,
f(x) = x9 + 4x7 + 11
On differentiating both sides with respect to x, we get
f'(x) = 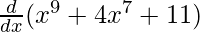
f'(x) = 9x8 + 28x6 + 0
f'(x) = 9x8 + 28x6
f'(x) = x6 (9x2 + 28)
As it is given, x ∈ R, we get,
=> x6 > 0
Also, we can conclude that,
=> 9x2 + 28 > 0
This gives us, f'(x) > 0.
Hence, the function is increasing on the interval x ∈ R.
Hence proved.
Question 21. Show that f(x) = x3 – 6x2 + 12x – 18 is increasing on R.
Solution:
We have,
f(x) = x3 – 6x2 + 12x – 18
On differentiating both sides with respect to x, we get
f'(x) = 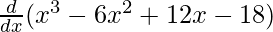
f'(x) = 3x2 – 12x + 12 – 0
f'(x) = 3x2 – 12x + 12
f'(x) = 3 (x2 – 4x + 4)
f'(x) = 3 (x – 2)2
Now for x ∈ R, we get,
=> (x – 2)2 > 0
=> 3 (x – 2)2 > 0
=> f'(x) > 0
Hence, the function is increasing on the interval x ∈ R.
Hence proved.
Question 22. State when a function f(x) is said to be increasing on an interval [a, b]. Test whether the function f(x) = x2 – 6x + 3 is increasing on the interval [4, 6].
Solution:
A function f(x) is said to be increasing on an interval [a, b] if f(x) > 0.
We have,
f(x) = x2 – 6x + 3
On differentiating both sides with respect to x, we get
f'(x) = 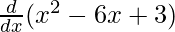
f'(x) = 2x – 6 + 0
f'(x) = 2x – 6
f'(x) = 2(x – 3)
Now for x ∈ [4, 6], we get,
=> 4 ≤ x ≤ 6
=> 1 ≤ (x – 3) ≤ 3
=> x – 3 > 0
=> f'(x) > 0
Thus, the function is increasing on the interval [4, 6].
Hence proved.
Question 23. Show that f(x) = sin x – cos x is an increasing function on (–π/4, π/4).
Solution:
We have,
f(x) = sin x – cos x
On differentiating both sides with respect to x, we get
f'(x) = 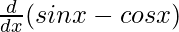
f'(x) = cos x + sin x
f'(x) = ![Rendered by QuickLaTeX.com \sqrt{2}[\frac{1}{\sqrt{2}}cosx+\frac{1}{\sqrt{2}}sinx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a8761a7adef7f4e394b9d0c27af4092_l3.png)
f'(x) = ![Rendered by QuickLaTeX.com \sqrt{2}[sin\frac{\pi}{4}cosx+cos\frac{\pi}{4}sinx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b522ca3fa241ae5a5e55bb29ae9abb8_l3.png)
f'(x) = 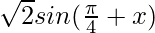
Now we have, x ∈ (–π/4, π/4)
=> –π/4 < x < π/4
=> 0 < (x + π/4) < π/2
=> sin 0 < sin (x + π/4) < sin π/2
=> 0 < sin (x + π/4) < 1
=> sin (x + π/4) > 0
=> √2 sin (x + π/4) > 0
=> f'(x) > 0
Thus, the function is increasing on the interval (–π/4, π/4).
Hence proved.
Question 24. Show that f(x) = tan–1 x – x is a decreasing function on R.
Solution:
We have,
f(x) = tan–1 x – x
On differentiating both sides with respect to x, we get
f'(x) = 
f'(x) = 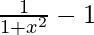
f'(x) = 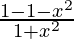
f'(x) = 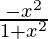
Now for x ∈ R, we have,
=> x2 > 0 and 1 + x2 > 0
=> 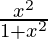 > 0
> 0
=> 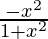 < 0
< 0
=> f'(x) < 0
Thus, f(x) is a decreasing function on the interval x ∈ R.
Hence proved.
Question 25. Determine whether f(x) = –x/2 + sin x is increasing or decreasing function on (–π/3, π/3).
Solution:
We have,
f(x) = –x/2 + sin x
On differentiating both sides with respect to x, we get
f'(x) = 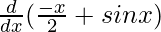
f'(x) = 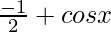
Now, we have
=> x ∈ (–π/3, π/3)
=> –π/3 < x < π/3
=> cos (–π/3) < cos x < cos (π/3)
=> 1/2 < cos x < 1/2
=> 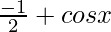 > 0
> 0
=> f'(x) > 0
Thus, f(x) is a increasing function on the interval x ∈ (–π/3, π/3).
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...