Class 11 RD Sharma Solutions – Chapter 25 Parabola – Exercise 25.1 | Set 2
Last Updated :
21 Jul, 2021
Question 11. Find the equation of the parabola whose focus is (5, 2) and having a vertex at (3, 2).
Solution:
Given that, the vertex of the parabola is (3, 2) and the focus of the parabola is (5, 2)
So, the slope of the axis of the parabola = 0
The slope of the directrix is not defined.
Let us assume the directrix intersect the axis at point K (r, s).
So, (r + 5)/2 = 3, (s + 2)/2 = 2
=> r = 1, s = 2
Hence, the equation of the directrix is x – 1 = 0 or x = 1.
Now, let us assume P (x, y) be any point on the parabola whose focus is S (5, 2).
And the equation of directrix is x =1.
So, the first we draw PM perpendicular to x = 1.
Then
SP = PM
SP2 = PM2
(x – 5)2 + (y – 2)2 = 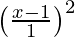
x2 + 25 – 10x + y2 + 4 – 4y = x2 + 1 – 2x
25 – 10x + y2 + 4 – 4y – 1 + 2x = 0
=> y2 – 4y – 8x + 28 = 0
Hence, the equation of the parabola is y2 – 4y – 8x + 28 = 0
Question 12. The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest wire being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.

Solution:
Given that the suspension cable forms a parabola with the vertex at (0, 6).
So, let us assume that the equation of the parabola formed by the suspension cable be,
(x – 0)2 = 4a (y – 6)
And it passes through point P (−50, 30) and Q (50, 30).
So, 2500 = 4a (30 – 6)
=> 4a = 2500/24
By putting the value of 4a in the given equation, we get
x2 = (2500/24) (y – 6)
Now, let the coordinates be (18, l) and it lies on the parabola (2).
So, 182 = (2500/24) (l – 6)
=> 324 = (2500/24) (l – 6)
=> l = 9.11 m
Therefore, 9.11 m is the supporting wire attached to the roadway 18 m from the middle.
Question 13. Find the equations of the lines joining the vertex of the parabola y2 = 6x to the point on it which have abscissa 24.
Solution:
Let us assume A and B be points on the parabola y2 = 6x.
Now, OA, OB be the lines joining the vertex O to the points A and B whose abscissa is 24.
Now,
=> y2 = 6 × 24
=> y2 = 144
=> y = ± 12
So, the coordinates of the points A is (24, 12) and B is (24, –12).
Hence, the equation of lines are
=> 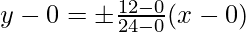
=> ±2y = x
Question 14. Find the coordinates of points on the parabola y2 = 8x whose focal distance is 4.
Solution:
Given that, the parabola is y2 = 8x
⇒ y2 = 4(2)x
Now, on comparing it with the general equation of parabola y2 = 4ax, we will get a = 2.
Let us assume that the required point be (x1, y1).
Also, given that focal distance is 4
=> x1 + a = 4
=> x1 + 2 = 4
=> x1 = 2
Now, this point satisfy the equation of parabola,
So, (y1)2 = 8(2) = 16
=> y12 = 16
=> y1 = ± 4
Hence, the coordinates of the points are (2, 4) and (2, −4).
Question 15. Find the length of the line segment joining the vertex of the parabola y2 = 4ax and a point on the parabola where the line segment makes an angle θ to the x-axis.
Solution:
Let us assume that the coordinates of the point on the parabola is B (x1, y1) and BO be the line segment in the parabola.
Now, in triangle AOB,
cos θ = AO/OB and sin θ = AB/OB
=> cos θ = x1/OB and sin θ = y1/OB
x1 = OB cos θ and y1 = OB sin θ
Now, the curve is passing through point (x1, y1)
So, (y1)2 = 4a(x1)
=> (OB sin θ)2 = 4a (OB cos θ)
=> (OB)2 sin2 θ = 4a OB cos θ
=> OB = 4a cos θ/sin2 θ
=> OB = 4a cosec θ cot θ
Therefore, the required length is 4a cosec θ cot θ.
Question 16. If the points (0, 4) and (0, 2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
Solution:
Given that the vertex of the parabola is (0, 4) and the focus of the parabola is (0, 2)
From the points we conclude that the vertex and focus lie on y-axis, so y-axis is the axis of the parabola.
Now, if the directrix meets the axis of the parabola at point Z, then AZ = AF = 2.
OZ = OF + AZ + FA
= 2 + 2 + 2
= 6
So, the equation of the directrix is y = 6.
i.e., y − 6 = 0
Let us assume P(x, y) be any point in the plane of the focus and directrix.
And MP be the perpendicular distance from P to the directrix, then P lies on parabola if FP = MP.
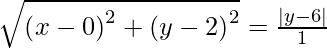
x2 + y2 – 4y + 4 = y2 – 12y + 36
=> x2 + 8y = 32
Hence, the equation of the parabola is x2 + 8y = 32
Question 17. If the line y = mx + 1 is tangent to the parabola y2 = 4x, then find the value of m.
Solution:
Given that the equation of the is y2 = 4x.
On substituting the value of y = mx + 1 in the equation of parabola, we get
(mx + 1)2 = 4x
⇒ m2x2 + 2mx + 1 = 4x
⇒ m2x2 + (2m − 4)x + 1 = 0
As we know that a tangent touches the curve at a point, so the roots of the equation must be equal.
So, D = 0
=> (2m − 4)2 − 4m2 = 0
=> 4m2 −16m + 16 − 4m2 = 0
=> m = 1
Therefore, the value of m is 1.
Question 18. Find the distance between the vertex and focus of the parabola y2 + 6y + 2x + 5 = 0.
Solution:
Given that the equation of the parabola is y2 + 6y + 2x + 5 = 0
(y + 3)2 + 2x – 4 = 0
(y + 3)2 = -2 (x – 2)
Let us assume Y = y + 3 and X = x – 2.
Now we get
Y2 = – 2X
On putting 4a = 2, we get
=> a = 1/2
Focus = (X = -1/2, Y = 0) = (x = 3/2, y = – 3)
Vertex = (X = 0, Y = 0) = (x = 2, y = -3)
So,
Focus = (3/2, -3)
Vertex = (2, -3)
Now, we find the distance between the vertex and the focus is,
D = 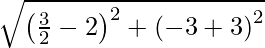
= 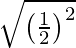
= 1/2 units
Therefore, the required distance is 1/2 units.
Question 19. Find the equation of the directrix of the parabola x2 − 4x − 8y + 12 = 0.
Solution:
Given that the equation of the parabola is x2 − 4x − 8y + 12 = 0
(x – 2)2 – 4 – 8y + 12 = 0
(x – 2)2 = 8 (y – 1)
Let us assume Y = y − 1 and X = x – 2.
Now we get
X2 = 8Y
Now, on comparing with x2 = 4ay, we get
=> a = 2
So, Directrix = Y = −a
=> y − 1 = −a
=> y = −a + 1
=> y = −2 + 1
=> y = −1
Therefore, the required equation of the directrix is y = -1.
Question 20. Write the equation of the parabola with focus (0, 0) and directrix x + y − 4 = 0.
Solution:
Given that the focus (0, 0) and directrix x + y − 4 = 0 of the parabola
Now, let us assume P (x, y) be any point on the parabola with the given focus and directrix
So, first we draw PM perpendicular to x + y = 4.
Then,
SP = PM
SP2 = PM2
(x – 0)2 + (y – 0)2 = 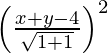
x2 + y2 = 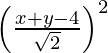
2x2 + 2y2 = x2 + y2 + 16 + 2xy – 8y – 8x
=> x2 + y2 – 2xy + 8x + 8y – 16 = 0
Hence, the equation of the parabola is x2 + y2 – 2xy + 8x + 8y – 16 = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...