Class 11 RD Sharma Solutions – Chapter 28 Introduction to 3D Coordinate Geometry – Exercise 28.3
Last Updated :
16 May, 2021
Question 1. The vertices of the triangle are A(5, 4, 6), B(1, -1, 3), and C(4, 3, 2). The internal bisector of angle A meets BC at D. Find the coordinates of D and the Length AD.
Solution:
We know that the angle bisector divides opposite side in ratio of other two sides
⇒D divides BC in ratio of AB:AC
A(5, 4, 6), B(1, -1, 3) and C(4, 3, 2)
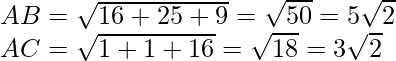
AB:AC=5:3=m:n
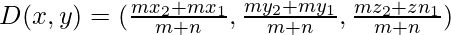
Substitute values for m:n=5:3
(x1,y1,z1)=(1,-1,3)
(x2,y2,z2)=(4,3,2)
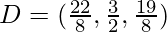
Question 2. A point C with z-coordinate 8 lies on the line segment joining the points A(2, -3, 4) and B(8, 0, 10). Find its coordinates.
Solution:
Z-coordinate 8
A(2, -3, 4) and B(8, 0, 10)
DR’s of AB=(6,3,6)
DR’s of BC=(x-8,y-0,8-10)
Given A,B,C lie on same line
So values of DR’s should be proportional
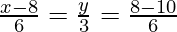
So x=6, y=-1
point is (6,-1,8)
Question 3. Show that three points A(2, 3, 4), B(-1, 2, -3) and C(-4, 1, -10) are collinear and find the ratio in which C divides AB.
Solution:
If points are collinear then all points lie on same line
and DR’s should be proportional
A(2, 3, 4), B(-1, 2, -3) and C(-4, 1, -10)
DR’s of AB=(3,1,7)
DR’s of BC=(3,1,7)
So A,B,C are collinear
Length of AC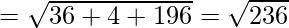
Length of AB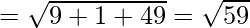
Ratio is AC:AB=2:1
So C divides AB in ratio 2:1 externally
Question 4. Find the ratio in which the line joining (2, 4, 5) and (3, 5, 4) is divided by the yz-plane.
Solution:
yz plane means x=0
Given (2,4,5) and (3,5,4)
Assume ratio to be m:n
Lets equate x term
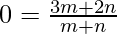
3m=-2n
m:n=-2:3
Which means yz plane divides the line in 2:3 ratio externally.
Question 5. Find the ratio in which the line segment joining the points (2, -1, 3) and (-1, 2, 1) is divided by the plane x+ y + z = 5.
Solution:
(2, -1, 3) and (-1, 2, 1)
x+y+z=5
Assume plane divides line in ratio λ:1
so point P which is dividing line in λ:1 ratio is
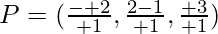
P lies on plane x+y+z=5
-λ+2+2λ-1+λ+3=5λ5
3λ=-1⇒λ=-1:3
Question 6. If the points A(3, 2, -4), B(9, 8, -10), and C(5, 4, -6) are collinear, find the ratio in which C divides AB.
Solution:
A(3, 2, -4), B(9, 8, -10) and C(5, 4, -6)
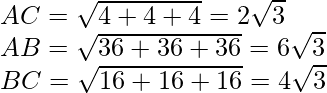
AC:BC=1:2
Question 7. The mid-points of the sides of a triangle ABC are given by (-2, 3, 5), (4, -1, 7), and (6, 5, 3). Find the coordinates of A, B, and C.
Solution:
Given midpoints (-2, 3, 5), (4, -1, 7) and (6, 5, 3)
Assume D is midpoint of AB, E is midpoint of BC
F is midpoint of CA
A(x1,y1,z1) B(x2,y2,z2) C(x3,y3,z3)
From midpoint formula, we get following equations
x1+x2=-4; x2+x3=8; x3+x1=12
y1+y2=6; y2+y3=-2; y3+y1=10
z1+z2=10; z2+z3=14; z3+z1=6
Solving above set of equations we get
A=(0,9,1)
B=(-4,-3,9)
C=(12,1,5)
Question 8. A(1, 2, 3), B(0, 4, 1), C(-1, -1, -3) are the vertices of a triangle ABC. Find the point in which the bisector of the angle ∠BAC meets BC.
Solution:
A(1, 2, 3), B(0, 4, 1), C(-1, -1, -3)
Angle bisector at A divides BC in ratio of AB:AC
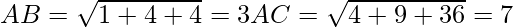
Assume D divides BC
so 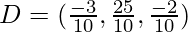
Question 9. Find the ratio in which the sphere x2+y2 +z2 = 504 divides the line joining the points (12, -4, 8) and (27, -9, 18).
Solution:
(12, -4, 8) and (27, -9, 18)
Assume point P is dividing line λ:1 ratio, we get
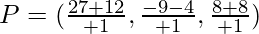
P lies on sphere, so substitute in sphere equation
x2+y2+z2=504
9(λ+4)2+(9λ+4)2+4(9λ+4)2=504(λ+1)2
729λ2+81λ2+324λ2+648λ+72λ+288λ+144+16+64=504λ2+1008λ+504
(1134-504)λ2+(1008-1008)λ+224-504=0
630λ2=280
λ2=4/9
λ=2:3
Question 10. Show that the plane ax + by + cz + d = 0 divides the line joining the points (x1,y1,z1) and (x2,y2,z2) in the ratio 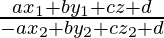
Solution:
Assume ratio is λ:1
Plane is ax+by+cz+d=0
points (x1,y1,z1) and (x2,y2,z2)
Assume point of intersection of line and plane is D
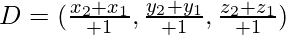
As D lies on plane, substitute D in plane equation, we get
λ(ax2+by2+cz2+d)+ax1+by1+cz1+d=0
⇒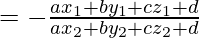
Question 11. Find the centroid of a triangle, mid-points of whose sides are (1, 2, -3), (3, 0, 1), and (-1, 1, -4).
Solution:
(1, 2, -3), (3, 0, 1) and (-1, 1, -4)
Centroid of triangle is given by
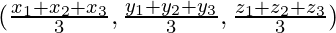
We know that
x1+x2=2
x2+x3=6
x1+x3=-2
Adding all gives ⇒2(x1+x2+x3)=6
so x1+x2+x3=3
Similarly, y1+y2+y3=3, z1+z2+z3=-6
centroid =(1,1,-2)
Question 12. The centroid of a triangle ABC is at the point (1, 1, 1). If the coordinate of A and B are (3, -5, 7) and (-1, 7, -6) respectively, find the coordinates of the point C.
Solution:
Given centroid (1,1,1)
A(3,-5,7) and B(-1,7,-6)
Equating terms, we get
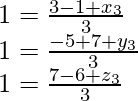
(x3,y3,z3)=(1,1,2)
Question 13. Find the coordinates of the points which trisect the line segment joining the points P(4, 2, -6) and Q(10, -16, 6).
Solution:
Trisection points are those which divide line in ratio 1:2 or 2:1
P(4, 2, -6) and Q(10, -16, 6)
Consider 1:2 case, we get
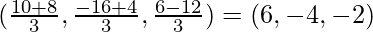
consider 2:! case, we get
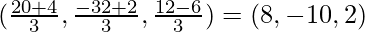
(6,-4,-2) and (8,-10,2) are trisection points
Question 14. Using section formula, show that the points A(2, -3, 4), B(-1, 2, 1) and C(0, 1/3, 2) are collinear.
Solution:
A(2, -3, 4), B(-1, 2, 1) and C(0, 1/3, 2)
DR’s of BC are 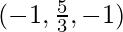
DR’s of AC are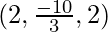
Its clear that all DR’s are proportional
Question 15. Given that P(3, 2, -4), Q(5, 4, -6), and R(9, 8, -10) are collinear. Find the ratio in which Q divides PR.
Solution:
P(3, 2, -4), Q(5, 4, -6) and R(9, 8, -10)
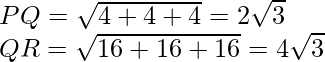
PQ:QR=1:2
Question 16. Find the ratio in which the line segment joining the points (4, 8, 10) and (6, 10, -8) is divided by the yz-plane.
Solution:
(4, 8, 10) and (6, 10, -8) is divided by the yz-plane
Equation of yz-plane is x=0
Assume ratio is m:n
Equating x-term, we get
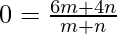
m:n=-2:3
So, XY plane divides the line segment in ratio 2:3 externally.
Share your thoughts in the comments
Please Login to comment...