Class 11 RD Sharma Solutions – Chapter 28 Introduction to 3D Coordinate Geometry – Exercise 28.1

Question 1: Name the octants in which the following points lie:

(i) (5, 2, 3)

(ii) (-5, 4, 3)

(iii) (4, -3, 5)

(iv) (7, 4, -3)

(v) (-5, -4, 7)

(vi) (-5, -3, -2)

(vii) (2, -5, -7)

(viii) (-7, 2, -5)

Solution:

(i) (5, 2, 3)

Here, since x, y and z all three are positive then octant will be XOYZ

(ii) (-5, 4, 3)

Here, since x is negative and y and z are positive then the octant will be X′OYZ

(iii) (4, -3, 5)

In this case, since y is negative and x and z are positive then the octant will be XOY′Z

(iv) (7, 4, -3)

Here, since z is negative and x and y are positive then the octant will be XOYZ′

(v) (-5, -4, 7)

Here, since x and y are negative and z is positive then the octant will be X′OY′Z

(vi) (-5, -3, -2)

Here, since x, y and z all three are negative then octant will be X′OY′Z′

(vii) (2, -5, -7)

Here, since z and y are negative and x is positive then the octant will be XOY′Z′

(viii) (-7, 2, -5)

Here, since x and z are negative and x is positive then the octant will be X′OYZ′

Question 2: Find the image of:

(i) (-2, 3, 4) in the yz-plane

(ii) (-5, 4, -3) in the xz-plane

(iii) (5, 2, -7) in the xy-plane

(iv) (-5, 0, 3) in the xz-plane

(v) (-4, 0, 0) in the xy-plane

Solution:

(i) (-2, 3, 4)

We can change the x-coordinate in order to find the corresponding image in the yz plane.

Hence, Image of point (-2, 3, 4) is (2, 3, 4)

(ii) (-5, 4, -3)

We can change the y-coordinate in order to find the corresponding image in the xz plane.

Here, Image of point (-5, 4, -3) is (-5, -4, -3)

(iii) (5, 2, -7)

We can change the z-coordinate in order to find the corresponding image in the xy plane.

Here, Image of point (5, 2, -7) is (5, 2, 7)

(iv) (-5, 0, 3)

We can change the y-coordinate in order to find the corresponding image in the xz plane.

Here, Image of point (-5, 0, 3) is (-5, 0, 3)

(v) (-4, 0, 0)

We can change the z-coordinate in order to find the corresponding image in the xy plane.

Here, Image of point (-4, 0, 0) is (-4, 0, 0)

Question 3: A cube of side 5 has one vertex at the point (1, 0, 1), and the three edges from this vertex are, respectively, parallel to the negative x and y-axes and positive z-axis. Find the coordinates of the other vertices of the cube.

Solution:

Given: 

A cube has side 4 having one vertex at (1, 0, 1)

Side of cube = 5

We have to find the coordinates of the other vertices of the cube.

So, 

Let the Point A(1, 0, 1) and AB, AD and AE is parallel to –ve x-axis, -ve y-axis and +ve z-axis respectively.

Since side of cube = 5

Point B is (-4, 0, 1)

Point D is (1, -5, 1)

Point E is (1, 0, 6)

Now, EH is parallel to –ve y-axis

Point H is (1, -5, 6)

HG is parallel to –ve x-axis

Point G is (-4, -5, 6)

Now, again GC and GF is parallel to –ve z-axis and +ve y-axis respectively

Point C is (-4, -5, 1)

Point F is (-4, 0, 6)

Question 4: Planes are drawn parallel to the coordinates planes through the points (3, 0, -1) and (-2, 5, 4). Find the lengths of the edges of the parallelepiped so formed.

Solution:

Given:  

Points are (3, 0, -1) and (-2, 5, 4)

We have to find the lengths of the edges of the parallelepiped formed.

For point (3, 0, -1)

x₁ = 3, y₁ = 0 and z₁ = -1

For point (-2, 5, 4)

x₂ = -2, y₂ = 5 and z₂ = 4

Plane parallel to coordinate planes of x₁ and x₂ is yz-plane

Plane parallel to coordinate planes of y₁ and y₂ is xz-plane

Plane parallel to coordinate planes of z₁ and z₂ is xy-plane

Distance between planes x₁ = 3 and x₂ = -2 is 3 – (-2) = 3 + 2 = 5

Distance between planes x₁ = 0 and y₂ = 5 is 5 – 0 = 5

Distance between planes z₁ = -1 and z₂ = 4 is 4 – (-1) = 4 + 1 = 5

Therefore,

The edges of parallelepiped is 5, 5, 5

Question 5: Planes are drawn through the points (5, 0, 2) and (3, -2, 5) parallel to the coordinate planes. Find the lengths of the edges of the rectangular parallelepiped so formed.

Solution:

Given:  

Points are (5, 0, 2) and (3, -2, 5)

We have to find the lengths of the edges of the parallelepiped formed

For point (5, 0, 2)

x₁ = 5, y₁ = 0 and z₁ = 2

For point (3, -2, 5)

x₂ = 3, y₂ = -2 and z₂ = 5

Plane parallel to coordinate planes of x₁ and x₂ is yz-plane

Plane parallel to coordinate planes of y₁ and y₂ is xz-plane

Plane parallel to coordinate planes of z₁ and z₂ is xy-plane

Distance between planes x₁ = 5 and x₂ = 3 is 5 – 3 = 2

Distance between planes y₁ = 0 and y₂ = -2 is 0 – (-2) = 0 + 2 = 2

Distance between planes z₁ = 2 and z₂ = 5 is 5 – 2 = 3

Therefore,

The edges of parallelepiped is 2, 2, 3

Question 6: Find the distances of the point P (-4, 3, 5) from the coordinate axes.

Solution:

Given:

The point P (-4, 3, 5)

The distance of the point from x-axis is given as:

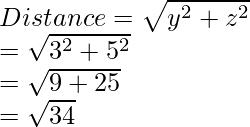
The distance of the point from y-axis is given as:

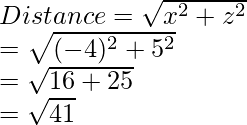
The distance of the point from z-axis is given as:

Question 7: The coordinates of a point are (3, -2, 5). Write down the coordinates of seven points such that the absolute values of their coordinates are the same as those of the coordinates of the given point.

Solution:

Given:  

Point (3, -2, 5)

The Absolute value of any point(x, y, z) is shown by,

√(x² + y² + z²)

We need to make sure that absolute value to be the same for all points.

So let the point A(3, -2, 5)

Remaining 7 points are:

Point B(3, 2, 5) (By changing the sign of y coordinate)

Point C(-3, -2, 5) (By changing the sign of x coordinate)

Point D(3, -2, -5) (By changing the sign of z coordinate)

Point E(-3, 2, 5) (By changing the sign of x and y coordinate)

Point F(3, 2, -5) (By changing the sign of y and z coordinate)

Point G(-3, -2, -5) (By changing the sign of x and z coordinate)

Point H(-3, 2, -5) (By changing the sign of x, y and z coordinate)