Question 23. Prove that the points (a, 0), (0, b) and (1, 1) are collinear if, 1/a + 1/b = 1.
Solution:
Let us assume that the points are A (a, 0), B (0, b) and C (1, 1) form a triangle ABC
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[a(b – 1) + 0(1 – 0) + 1(0 – b)]
= 1/2[ab – a + 0 + 1(-b)]
= 1/2[ab – a – b]
If the points are collinear, then area of ∆ABC = 0
⇒1/2(ab – a – b) = 0
⇒ab – a – b = 0
⇒ ab = a + b
Now on dividing by ab, we get
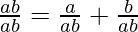
⇒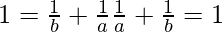
Question 24. Point A divides the join of P (-5, 1) and Q (3, 5) in the ratio k : 1. Find the two values of k for which the area of ∆ABC where B is (1, 5) and C (7, -2) is equal to 2 units.
Solution:
Let us assume that the coordinates of A be (x, y) which divides the join of P (-5, 1) and Q (3, 5) in the ratio.
So, the coordinates of A will be 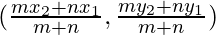
Or 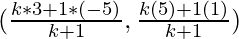 or
or 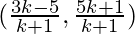
It is given that area of ∆ABC is 2 units and vertices are B(1, 5), C(7, -2) and A are the vertices
So, Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
⇒![Rendered by QuickLaTeX.com 2=\frac{1}{2}[\frac{3k-5}{k+1}(5+2)+1(-2-\frac{5k+1}{k+1}+7(\frac{5k+1}{k+1}-5)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f575d0393ffc056326eb991ab1c9ab5_l3.png)
⇒![Rendered by QuickLaTeX.com 2=\frac{1}{2}[\frac{3k-5}{k+1}*7-2-\frac{5k+1}{k+1}+7(\frac{5k+1}{(k+1)-35})]\\ ⇒4=[\frac{21k-35}{k+1}-\frac{5k+1}{k+1}+\frac{35k+7}{k+1}-37]\\ ⇒4=[\frac{21k-35-5k+1+35k+7-37k-37}{k+1}]\\ ⇒|\frac{14k-66}{k+1}|=±4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b08a756e3725a30ff20a6e4c4ddbebf1_l3.png)
(i) (14k – 66)(k + 1) = 4 ⇒ 14k – 66 = 4k + 4
⇒ 14k – 4k = 66 + 4
⇒10k = 70
⇒ k = 70/10 = 7
(ii) (14k – 66)(k + 1) = -4 ⇒ 14 – 66 = -4k – 4
⇒ 14k + 4k = -4 + 66 ⇒ 18k = 62
⇒ k = 62/18 = 31/9
Hence, the value of k is 7, 31/9
Question 25. The area of a triangle is 5. Two of its vertices are (2, 1) and (3, -2). The third vertex lies on y = x + 3. Find the third vertex.
Solution:
Let us considered ABC is a triangle whose vertices are (2, 1), (3, -2) and (x, y)
Also the area of triangle ABC is 5
So,
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
5 = 1/2[x(1 + 2) + 2(-2 – y) + 3(y – 1)]
10 = [3x-4-2y+3y-3]
10 = 3x + y – 7
3x + y = 10 + 7
3x + y = 17
But it is given that the point (x, y) lies on y = x + 3
So, 3x + x + 3 = 17
⇒ 4x = 17 – 3
4x = 14
⇒ x = 7/2
and y = x + 3 = 7/2 +3 = 13/2
Hence, the third vertex is (7/2, 13/2)
Question 26. Four points A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x) are given in such a way that 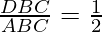 , find x?
, find x?
Solution:
Let us assume that ABCD is a quadrilateral whose vertices are A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x)
Now, AC and BD are joined
Area of triangle = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [6(5 + 2) + (-3)(-2 – 3) + 4(3 – 5)]
= 1/2 [6 * 7 + (-3)(-5) + 4(-2)]
= 1/2 [42 + 15 – 8] = 49/2
and area of △DBC,
= 1/2[x(5 + 2) + (-3)(-2 – 3x) + 4(3x – 5)]
= 1/2[7x + 6 + 9x + 12x – 20]
= 1/2[28x – 14] = 14x – 7
Now,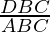 [Tex]=\frac{14x-7}{\frac{49}{2}} [/Tex]
[Tex]=\frac{14x-7}{\frac{49}{2}} [/Tex]
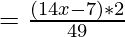
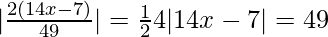
If 56x – 28 = 49
⇒ 56x = 49 + 28 = 77
⇒ x = 77/56 = 11/8
If 4(14x – 7) = 49
⇒56x – 28 = -49
⇒56x = -49 + 28 = -21
⇒x = -21/56 = -3/8
x = 11/8 or -3/8
Question 27. If three points (x1, y1), (x2, y2), (x3, y3) lie on the same line, prove that
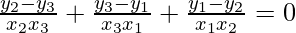
Solution:
Let us assume that ABC is a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3)
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
The points be on the same line, so
[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)] = 0
On dividing by x1 x2 x3, we get
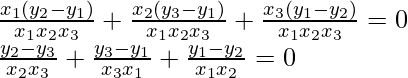
Question 28. Find the area of a parallelogram ABCD if three of its vertices are A (2, 4), B (2 + √3, 5) and C (2, 6).
Solution:
Given that ABCD is a ||gm whose vertices are A (2, 4), B (2 + √3, 5) and C (2, 6).
Now draw one diagonal AC of ||gm ABCD
Diagonal bisects the ||gm into two triangle equal in area
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [2(5 – 6) + (2 + √3)(6 – 4) + 2(4 – 5)]
= 1/2 [2 * (-1) + (2 + √3) * 2 + 2 * (-1)]
= 1/2 [-2 + 4 + 2√3 – 2] = 1/2 (2√3) = √3sq.units
So, the area of ||gm ABCD = 2 * area(△ABC)
= 2 * (√3) = 2√3 sq.units
Question 29. Find the value (s) of k for which the points (3k – 1, k – 2), (k, k – 7), and (k – 1, -k – 2) are collinear.
Solution:
Let us assume that the ABC is a triangle whose vertices are A(3k – 1, k – 2), B(k, k – 7) and C(k – 1, -k – 2)
and A, B, C are collinear
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[(3k – 1)(k – 7 + k + 2) + k(-k – 2 – k + 2) + (k – 1)(k – 2 – k + 7)]
= 1/2 [(3k – 1)(2k – 5) + k(-2k + (k – 1) * 5)]
= 1/2 [6k2 – 15k – 2k + 5 – 2k2 + 5k – 5]
= 1/2[4k2 – 12k] = 2k2 – 6k
= 2k(k – 3)
As we know that the points are collinear
so, Area of ABC=0
2k(k – 3) = 0
Either 2k = 0 or k – 3 = 0, then k = 0 or k = 3
Therefore, k = 0, 3
Question 30. If the points A (-1, -4), B (b, c) and C (5, -1) are collinear and 2b + c = 4, find the values of b and c.
Solution:
Let us assume that the ABC is a triangle whose vertices are A (-1, -4), B (b, c) and C (5, -1)
and A, B, C are collinear
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [-1(c + 1) + b(-1 + 4) + 5(-4 – c)]
= 1/2 [-c – 1 – b + 4b – 20 – 5c]
= 1/2 [3b – 6c – 21]
As we know that the points are collinear
so, Area of triangle ABC = 0
1/2(2b – 6c – 21) = 0
⇒3b – 6c = 21
3b – 6c = 21 ———–(i)
and 2b + c = 4 ———-(ii)
⇒c = 4 – 2b
On substituting the value of c in eq (i), we get
⇒3b – 6(4 – 2b) = 21
⇒3b – 24 + 12b = 21
15b = 21 + 24 = 45
⇒b = 45/15 = 3
c = 4 – 2b = 4 – 2 * 3 = 4 – 6 = -2
b = 3, c = -2
Question 31. If the points A (-2, 1), B (a, b), and C (4, -1) are collinear and a – b = 1, find the values of a and 6.
Solution:
Let us assume that the ABC is a triangle whose vertices are A (-2, 1), B (a, b), and C (4, -1)
and A, B, C are collinear
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [-2(b + 1) + a(-1 – 1) + 4(1 – b)]
= 1/2[-2b – 2 – 2a + 4 – 4b]
= 1/2 [-2b – 2 – 2a + 4 – 4b]
= 1/2 [-2a – 6b + 2] = -a – 3b + 1
As we know that the points are collinear
so, Area of triangle ABC = 0
-a – 3b + 1 = 0
a + 3b = 1 ————(i)
a = 1 – 3b
and given that a – b = 1 ————(ii)
On solving eq(i) and (ii), we get
4b = 0 ⇒ b = 0
Therefore, a = 1 – 3b = 1 – 3 * 0 = 1 – 0 = 1
a = 1, b = 0
Question 32. If the points A (1, -2), B (2, 3), C (a, 2), and D (-4, -3) form a parallelogram, find the value of a and height of the parallelogram taking AB as a base.
Solution:

Given that ABCD is a parallelogram whose vertices are A (1, -2), B (2, 3), C (a, 2), and D (-4, -3)
As we know that, diagonals bisects each other
i.e., mid-point of AC = mid-point of BD
⇒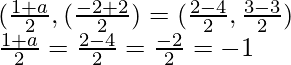
= 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
⇒1 + a = -2
⇒a = -3
So, the required value of a is -3
Given that, AB as base of a ||gm and drawn a perpendicular from A to AB
which meet AB at P. So, DP is a height of a ||gm.
Now, equation of base AB, passing through the points (1, -2) and (2, 3) is
⇒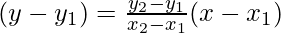
⇒(y + 2)=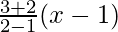
⇒(y + 2) = 5(x – 1)
⇒5x – y = 7 ————(i)
So, the slope of AB, say 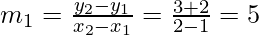
Let the slope of DP be m2.
Since, DP is perpendicular to AB.
By condition of perpendicularity
m1 * m2 = -1 ⇒ 5 * m2 = -1
⇒m2 = -1/5
Now, eq. of DP, having slope (-1/5)
and passing the point (-4,-3) is (y – y1) = m2(x – x1)
⇒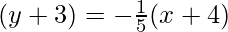
⇒5y + 15 = -x – 4
⇒x + 5y = -19 ————-(ii)
On adding eq (i) and (ii), then we get the intersection point P.
Now put the value of y from eq. (i) in eq. (ii), we get
x + 5(5x – 7) = -19 [using Eq. (i)]
⇒x + 25x – 35 = -19
⇒26x = 16
x = 8/13
Now put the value of x in Eq.(i), we get
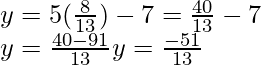
So, the coordinates of point P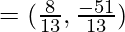
And, the length of the height of a parallelogram,
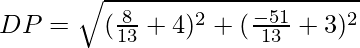
Now, by using distance formula, we get
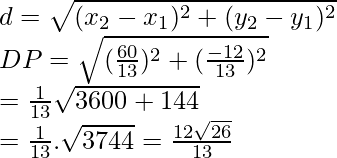
Hence, the required length of height of a parallelogram is 12√26/13
Question 33. A (6, 1), B (8, 2) and C (9, 4) are three vertices of a parallelogram ABCD. If E is the mid-point of DC, find the area of ∆ADE.
Solution:
Given that, ABCD is a parallelogram, whose vertices are A (6,1), B (8,2) and C (9,4)
Let us assume that the fourth vertex of parallelogram be D(x, y).
Now as we know that, the diagonal of a parallelogram bisect each other.
so, Mid point of BD = Mid point of AC
⇒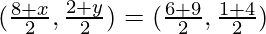
⇒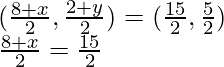
⇒8+x=15⇒x=7
and 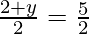
⇒2 + y = 5 ⇒ y = 3
So, fourth vertex of ||gm is D(7, 3)
Now, mid-point of side DC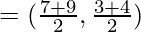
E = (8, 7/2)
Now we find the area of ∆ADE
= 1/2[6(3 – 7/2) + 7(7/2 – 1) + 8(1 – 3)]
= 1/2 [6 * (-1/2 + 7(5/2 + 8(-2)]
= 1/2 (-3 + 35/2 – 16)
= 1/2 ( 35/2 – 19)
= 1/2 (-3/2)
= -3/4 [As we know that area cannot be negative]
Hence, the required area ∆ADE is 3/4sq. units
Question 34. If D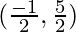 E (7, 3) and F
E (7, 3) and F 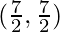 are the mid-points of sides of ∆ABC, find the area of ∆ABC.
are the mid-points of sides of ∆ABC, find the area of ∆ABC.
Solution:

Given that ABC is a triangle, so let us assume that the vertices of triangle ABC are A(x1, y1), B(x2, y2) and C(x3, y3)
And the mid points of side BC, CA, and AB are D(-1/2, 5/2), E(7, 3), and F(7/2, 7/2)
Since, D(-1/2, 5/2) is the mid-point of BC.
So, 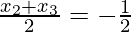
and 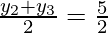
⇒x2 + x3 = -1 ————(i)
and y2 + y3 = 5
As we know that E(7, 3) is the mid-point of CA.
So, 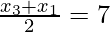 and
and 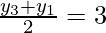
⇒x3 + x1 = 14 ———–(iii)
and y3 + y1 = 6 ————(iv)
Also, F(7/2, 7/2) is the mid-point of AB 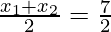
and 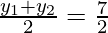
⇒x1 + x2 = 7 ————–(v)
and y1 + y2 = 7 —————-(vi)
Now on adding Eq.(i), (ii) and (v), we get
2(x1 + x2 + x3) = 20
x1 + x2 + x3 = 10 —————(vii)
On subtracting Eq. (i) (iii) and (v) from Eq. (vii), we get
x1 = 11, x2 = -4, x3 = 3
On adding Eq.(ii), (iv) and (vi), we get
2(y1 + y2 + y3) = 18
⇒y1 + y2 + y3 = 9 ————-(viii)
On subtracting Eq. (ii), (iv) and (vi) from Eq. (viii), we get
y1 = 4, y2 = 3, y3 = 9
Hence, the vertices of ∆ABC are A(11, 4), B(-4, 3) and C(3, 2)
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[11(3 – 2) + (-4)(2 – 4) + 3(4 – 3)]
= 1/2[11 * 1 + (-4)(-2) + 3(1)]
= 1/2(11 + 8 + 3)
= 22/2 = 11
Hence, the required area of ∆ABC is 11 sq.unit
Share your thoughts in the comments
Please Login to comment...