Question 40. Prove that the points (3, 0), (4, 5), (-1, 4), and (-2, -1) taken in order, form a rhombus. Also, find its area.
Solution:
Let us considered the given points are A(3, 0), B(4, 5), C(-1, 4) and D(-2, -1)
Now we find the length of the sides and diagonals,
By using distance formula
So, AB = 
AB2 = (4 + 3)2 + (5 – 0)2
= (1)2 + (5)2
= 1 + 25 = 26
Similarly, BC2 = (-1 – 4)2 + (4 – 5)2
= (-5)2 + (-1)2 = 25 + 1 = 26
CD2 = (-2 + 1)2 + (-1 – 4)2
= (-1)2 + (-5)2 = 1 + 25 = 26
and DA2 = (3 + 2)2 + (0 + 1)2
= (5)2 + (1)2 = 25 + 1 = 26
Diagonal AC2 = (-1 – 3)2 + (4 – 0)2
= (-4)2 + (4)2 = 16 + 16 = 32
and BD2 = (-2 – 4)2 + (-1 – 5)2
= (-6)2 + (-6)2 = 36 + 36 = 72
So, we conclude that the sides AB = BC = CD = DA and diagonal AC is not equal to BD
Hence, ABCD is a rhombus
Now we find the area of rhombus ABCD = Product of diagonals/2
= (√32 × √72)/2
= (√16 × 2 × 2 × 36)/2
= 4 × 2 × 6/2
= 24 sq. units
Question 41. In the seating arrangement of desks in a classroom three students Rohini, Sandhya, and Bina are seated at A (3, 1), B (6, 4), and C (8, 6). Do you think they are seated in a line?
Solution:
Given that A (3, 1), B (6, 4) and C (8, 6)
Now we find the length of the sides and diagonals,
By using distance formula
AB = 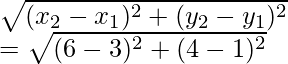
AB2 = (6 – 3)2 + (4 – 1)2
= (3)2 + (3)2 = 9 + 9 = 18
Similarly, BC2 = (8 – 6)2 + (6 – 4)2
= (2)2 + (2)2 = 4 + 4 = 8
and BC2 = (8 – 6)2 + (6 – 4)2
= (2)2 + (2)2 = 4 + 4 = 8
and CA2 = (3 – 8)2 + (1 – 6)2
= (-5)2 + (-5)2 = 25 + 25 = 50
AB = √18 = √9 * 2 = 3√2
BC = √8 = √4 * 2 = 2√2
and CA = √50 = √25 * 2 = 5√2
AB + BC = 3√2 + 2√2 = 5√2 = CA
Hence, A, B and C are collinear points. Hence, they are seated in a line.
Question 42. Find a point on y-axis which is equidistant from the points (5, -2) and (-3, 2).
Solution:
Let us assume P be the point lies on y-axis. So, its x = 0, so the coordinates of P is (0, y)
It is given that the point P (0, y) is equidistant from the points A(5, -2) and B(-3, 2).
So, PA = PB
Also, PA2 = PB2
Now by using distance formula, we get
(5 – 0)2 + (-2 – y)2 = (-3 – 0)2 + (2 – y)2
25 + 4 + y2 + 4y = 9 + 4 – 4y + y2
y2 + 4y + 4y – y2 = 13 – 29
8y = -16
y = -16/8 = 2
Hence, the required point P is (0,-2)
Question 43. Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4).
Solution:
Let us considered P (x, y) is equidistant from A(3, 6) and B(-3, 4)
So, PA = PB
Also, PA2 = PB2
Now by using distance formula, we get
![Rendered by QuickLaTeX.com \sqrt{(x-3)^2+(y-6)^2}=\sqrt{[x-(-3)]^2+(y-4)^2}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54196ecc917cb16e90636e8b3bb30e73_l3.png)
On squaring both sides, we get
(x – 3)2 + (y – 6)2 = (x + 3)2 + (y – 4)2
x2 – 6x + 9 + y2 – 12y + 36 = x2 + 6x + 9 = y2 – 8y + 16
-6x – 12y + 45 = 6x – 8y + 25
-6x – 6x – 12y + 8y + 45 – 25 = 0
-12 – 4y + 20 = 0
3x + y – 5 = 0
3x + y = 5
Question 44. If a point A (0, 2) is equidistant from the points B (3, p) and C (p, 5), then find the value of p.
Solution:
Given that the point A (0, 2) is equidistant from the points B (3, p) and C (p, 5)
Now by using distance formula, we get
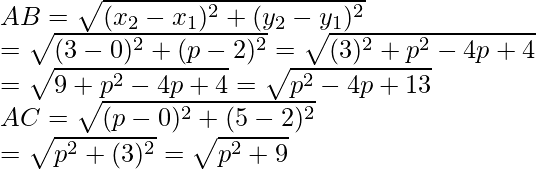
It is given that AB = AC
√p2 – 4p + 13 = √p2 + 9
So, on squaring both side, we get
= p2 – 4p + 13 = p2 + 9
p2 – 4p – p2 = 9 – 13
-4p = -4
p = 1
Hence, the value of p is 1
Question 45. Prove that the points (7, 10), (-2, 5), and (3, -4) are the vertices of an isosceles right triangle.
Solution:
Let us considered the points are A (7, 10), B (-2, 5) and C (3, -4)
Now we find the length of the sides
By using distance formula
Now AB = 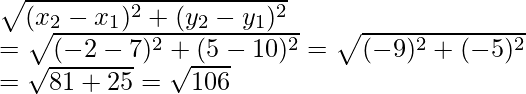
Similarly, BC = 
and AC = 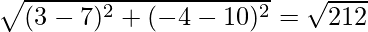
So, we conclude that AB = BC = √106 and AB2 + BC2 = AC2
Hence, ABC is an isosceles right triangle
Question 46. If the point P (x, 3) is equidistant from the points A (7, -1) and B (6, 8), find the value of x and the distance AP.
Solution:
It is given that Point P (x, 3) is equidistant from the points A (7, -1) and B (6, 8)
So, PA = PB
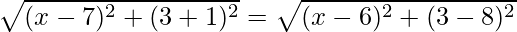
On squaring both sides, we get
(x – 7)2 + (4)2 = (x – 6)2 + (-5)2
x2 – 14x + 49 + 16 = x2 – 12x + 36 + 25
x2 – 14x + 65 = x2 – 12x + 61
x2 – 14x + 12x – x2 = 61 – 65
-2x = -4
x = -4/-2 = 2
x = 2
Now we find the distance 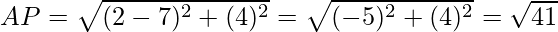
Question 47. If A (3, y) is equidistant from points P (8, -3) and Q (7, 6), find the value of y and find the distance AQ.
Solution:
It is given that point A (3, y) is equidistant from P (8, -3) and Q (7, 6)
So, AP = AQ
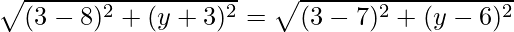
On squaring both sides, we get
(3 – 8)2 + (y + 3)2 = (-4)2 + (y – 6)2
(-5)2 + y2 + 6y + 9 = 16 + y2 – 12y + 36
25 + y2 + 6y + 9 = 16 + y2 – 12y + 36
y2 + 6y – y2 + 12y = 36 – 9 – 25 + 16
18y = 18
y = 18/18 = 1
y = 1
Now we find the distance 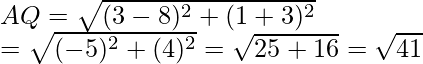
Question 48. If (0, -3) and (0, 3) are the two vertices of an equilateral triangle, find the coordinates of its third vertex.
Solution:

Given that the A (0, -3) and B (0, 3) are the two vertices of an equilateral triangle ABC
Let us assume that the coordinates of the third vertex be C (x, y)
In equilateral triangle, AC = AB
So,
(x – 0)2 + (y + 3)2 = (0 – 0)2 + (3 + 3)2
x2 + (y + 3)2 = 0 + (6)2 = 36
x2 + y2 + 6y + 9 = 36
x2 + y2 + 6y = 36 – 9 = 27 …….(i)
Also, BC = AB
(x – 0)2 + (y – 3)2 = 36
x2 + y2 + 9 – 6y = 36
x2 + y2 – 6y = 36 – 9 = 27 ……..(ii)
So, from eq (i) and (ii), we get
x2 + y2 + 6y = x2 + y2 – 6y
x2 + y2 + 6y – x2 – y2 + 6y = 0
12y = 0
y = 0
Now put the value of y in eq(i)
x2 + y2 + 6y = 27
x2 + 0 + 0 = 27
x = ±√27 = ±3√3
So, the coordinates of third point is(3√3, 0) or (-3√3, 0)
Question 49. If the point P (2, 2) is equidistant from the points A (-2, k) and B (-2k, -3), find k. Also, find the length of AP.
Solution:
Given that the point P (2, 2) is equidistant from the points A (-2, k) and B (-2k, -3)
So, AP = BP
(2 + 2)2 + (2 – k)2 = (2 + 2k)2 + (2 + 3)2
(4)2 + (2 – k)2 = (2 + 2k)2 + (5)2
16 + 4 + k2 – 4k = 4 + 4k2 + 8k + 25
4k2 + 8k + 29 – 16 – 4 – k2 + 4k = 0
3k2 + 12k + 9 = 0
k2 + 4k + 3 = 0
k2 + k + 3k + 3 = 0
k(k + 1) + 3(k + 1) = 0
(k + 1)(k + 3) = 0
So, the value of k either k + 1 = 0, then k = -1
or k + 3 = 0, then k = -3
Therefore, k = -1, -3
Now we find the distance 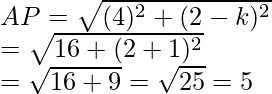
Question 50. Show that ∆ABC, where A (-2, 0), B (2, 0), C (0, 2) and ∆PQR, where P (-4, 0), Q (4, 0), R (0, 4) are similar.
Solution:
Given that In ∆ABC, the vertices are A (-2, 0), B (2, 0), C (0, 2)
In ∆PQR, the vertices are P (-4, 0), Q (4, 0), R (0, 4)
Show that ∆ABC ~ ∆PQR
So,

Now, 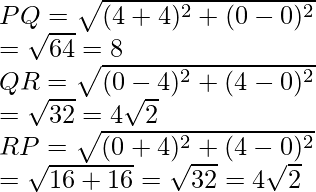
So, AB/PQ = 4/8 = 1/2
BC/QR = 2√2/4√2 = 1/2
CA/PQ = 2√2/4√2 = 1/2
So, AB/PQ = BC/QR = CA/RP
By using SSS
∆ABC ~ ∆PQR
Question 51. An equilateral triangle has two vertices at the points (3, 4), and (-2, 3). Find the coordinates of the third vertex.
Solution:

Given that the A (3, 4) and B (-2, 3) are the two vertices of an equilateral triangle ABC
Let us assume that the coordinates of the third vertex be C (x, y)
Now 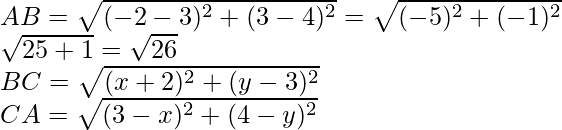
As we know that in equilateral triangle, AB = BC = CA
So, BC = AB
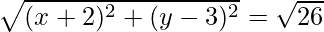
On squaring both side we get
(x + 2)2 + (y – 3)2 = 26
x2 + 4x + 4 + y2 – 6y + 9 = 26
x2 + y2 + 4x – 6y + 13 = 26
x2 + y2 + 4x – 6y = 26 – 13 = 12 ………..(i)
Similarly, CA = AB
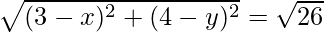
On squaring both side we get
(3 – x)2 + (4 – y)2 = 26
9 + x2 – 6x + 16 + y2 – 8y = 26
x2 + y2 – 6x – 8y + 25 = 26
x2 + y2 – 6x – 8y = 26 – 25 = 1 …….(ii)
Now on subtracting eq(ii) from (i), we get
10x + 2y = 12
5x + y = 6 ……..(iii)
y = 6 – 5x
Now substituting the value of y in eq(i), we get
x2 + (6 – 5x)2 + 4x – 6(6 – 5x) = 13
x2 + 36 + 25x2 – 60x + 4x – 36 + 30x – 13 = 0
26x2 – 26x – 13 = 0
2x2 – 2x – 1 = 0
Here, a = 2, b = -2, c = -1
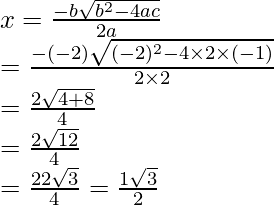
When x = (1 + √3)/2, then y = 6 – 5x = 6 – 5((1 + √3)/2) = (7 – 5√3)/2
Or when x = (1 – √3)/2, then y = 6 – 5x = 6 – 5((1 – √3)/2) = (7 + 5√3)/2
Hence, the co-ordinates of the point C is ((1 + √3)/2, (7 – 5√3)/2) or ((1 – √3)/2, (7 + 5√3)/2)
Question 52. Find the circumcenter of the triangle whose vertices are (-2, -3), (-1, 0), (7, -6).
Solution:

Given that the vertices of ∆ABC are A(-2, -3), B(-1, 0), and C(7, -6), and
let us assume that O is the circumcenter ∆ABC. So, the coordinates of O will be (x, y)
So, OA = OB = OC
Or OA2 = OB2 = OC2
Now 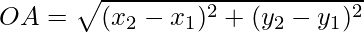
OA2 = (x + 2)2 + (y + 3)2
= x2 + 4x + 4 + y2 + 6y + 9
= x2 + y2 + 4x + 6y + 13
OB2 = (x + 1)2 + (y + 0)2
= x2 + 2x + 1 + y2
= x2 + y2 + 2x + 1
OC2 = (x – 7)2 + (y + 6)2
= x2 – 14x + 49 + y2 + 12y + 36
= x2 + y2 – 14x + 12y + 85
OA2 = OB2
x2 + y2 + 4x + 6y + 13 = x2 + y2 + 2x + 1
4x + 6y -2y = 1 – 13
2x + 6y = -12
x + 3y = -6 ………(i)
OB2 = OC2
x2 + y2 + 2x + 1 = x2 + y2 – 14x + 12y + 85
2x + 14x – 2y = 85 – 1
16x – 12y = 84
4x – 3y = 21 ………(ii)
From eq (i), we get
x = -3y – 6
On substituting the value of x in eq (ii)
4(-3y – 6) – 3y = 21
-12 – 24 – 3y = 21
-15y = 21 + 24
-15y = 45
y = -45/15 = -3
x = -3y – 6 = -3 × (-3) – 6
= + 9 – 6 = 3
Hence, the co-ordinates of O are (3,-3)
Question 53. Find the angle subtended at the origin by the line segment whose endpoints are (0, 100) and (10, 0).
Solution:
Let us considered the co-ordinates of the end points of a line segment are
A (0, 100), B (10, 0) and origin is O (0, 0)
So, the angle subtended by the line PQ at the origin is 90° or π/2
Question 54. Find the centre of the circle passing through (5, -8), (2, -9), and (2, 1).
Solution:

Given that O is the centre of the circle and A(5, -8), B(2, -9), and C (2, 1) are the points on the circle.
So, let us considered the co-ordinates of O be (x, y)
Therefore, OA = OB = OC
OA2 = OB2 = OC2
Now 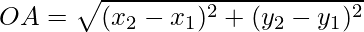
OA2 = (x – 5)2 + (y + 8)2
= x2 – 10x + 25 + y2 + 16y + 64
= x2 + y2 – 10x + 16y + 89
Similarly, OB2 = (x – 5)2 + (y + 9)2
= x2 + 4 – 4x + y2 + 81 + 18y
= x2 + y2 – 4x + 18y + 85
and OC2 = x2 – 4x + 4 + y2 – 2y + 1
= x2 + y2 – 4x – 2y + 5
OA2 = OB2
x2 + y2 – 10x + 16y + 89 = x2 + y2 – 4x + 18y + 85
-10x + 4x + 16y – 18y = 85 – 89
-6x – 2y = -4
3x + y = 2 …….(i)
OB2 = OC2
x2 + y2 – 4x + 18y + 85 = x2 + y2 – 4x – 2y + 5
18y + 2y = 5 – 85
20y = -80
y = -80/10 = -4
Now substitute the value of y in eq(i), we get
3x + y = 2
3x – 4 = 2
3x = 2 + 4 = 6
x = 6/3 = 2
Hence, the co-ordinates of O are(2,-4)
Question 55. If two opposite vertices of a square are (5, 4) and (1, -6), find the coordinates of its remaining two vertices.
Solution:

Given that the two opposite points of a ABCD square are A(5, 4) and C(1, -6)
Let us considered that the co-ordinates of B be (x, y).
So, join AC
As we know that the sides of a square are equal, so,
AB = BC
AB2 = BC2
(x – 5)2 + (y – 4)2 = (x – 1)2 + (y + 6)2
x2 – 10x + 25 + y2 – 8y + 16 = x2 – 2x + 1 +y2 + 12y + 36
-10x + 2x – 8y – 12y = 37 – 41
-8x – 20y = -4
2x + 5y = 1
2x = 1 – 5y
x = (1 – 5y)/2
So, ABC is a right-angled triangle
Now by using Pythagoras theorem, we get
AC2 = AB2 + BC2
(5 – 1)2 + (4 + 6)2 = x2 – 10x + 25 + y2 – 8y + 16 + x2 – 2x + 1 + y2 + 12y + 36
(4)2 + (10)2 = 2x2 + 2y2 – 12x + 4y + 78
16 + 100 = 2x2 + 2y2 – 12x + 4y + 78
2x2 + 2y2 – 12x + 4y + 78 – 16 – 100 = 0
2x2 + 2y2 – 12x + 4y – 38 = 0
x2 + y2 – 6x + 2y – 19 = 0 …..(i)
Now substituting x = (1 – 5y)/2 in eq(i), we get
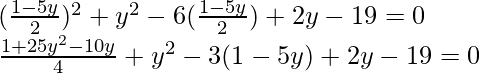
1 + 25y2 – 10y + 4y2 – 12 + 60y + 8y – 76 = 0
29y2 + 58y – 87 = 0
y2 + 2y – 3 = 0
y2 + 3y – y – 3 = 0
y(y + 3) – 1(y + 3) = 0
(y + 3)(y – 1) = 0
The value of y can be either y + 3 = 0, then y = -3
or y – 1 = 0, then y = 1
When y = 1, then
x = (1 – 5y)/2
= (1 – 5(1))/2
= -2
When y = -3, then
x = (1 – 5(-3))/2
= 8
So, the other points of ABCD square are(-2,1) and (8,-3)
Question 56. Find the centre of the circle passing through (6, -6), (3, -7), and (3, 3).
Solution:

Let us considered O be the centre of the circle is (x, y)
It is given that centre of the circle passing through (6, -6), (3, -7), and (3, 3)
Join OA, OB and OC
So, OA = OB = OC
OA2 = (x -6 )2 + (y + 6)2
OB2 = (x – 3)2 + (y + 7)2
and OC2 = (x – 3)2 + (y-3)2
As we know that OA2 = OB2
So, (x – 6)2 + (y + 6)2 = (x – 3)2 + (y + 7)2
x2 – 12x + 36 + y2+12y + 36 = x2 – 6x + 9 + y2 + 14y + 49
x2 – 12x + 36 + y2+12y + 36 – x2 + 6x – 9 – y2 – 14y – 49 = 0
-12x + 12y + 72 + 6x – 14y – 58 = 0
-6x – 2y + 14 = 0
-6x – 2y = -14
3x + y = 7 …..(i)
Also, OB2 = OC2
(x – 3)2 + (y + 7)2 = (x – 3)2 + (y – 3)2
x2 – 6x + 9 + y2+ 14y + 49 = x2 – 6x + 9 + y2 – 6y + 9
x2 + y2 – 6x + 58 + 14y – x2 – y2 + 6x + 6y – 18 = 0
20y + 40 = 0
20y = -40
y = -40/20 = -2
3x + (-2) = 7
3x = 7 + 2 = 9
x = 9/3 = 3
Hence, the co-ordinates of the centre are(3,-2)
Question 57. Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.
Solution:

Let us considered ABCD is square, in which the co-ordinates are A (-1, 2) and C (3, 2).
Let us assume the coordinates of B are (x, y)
Now, join AC
As we know that the sides of a square are equal, so,
AB = BC
AB2 = BC2
Now 
AB2 = (x + 1)2 + (y – 2)2
Similarly, BC2 = (x – 3)2 + (y – 2)2
As we know that AB = BC
So,
(x + 1)2 + (y – 2)2 = (x – 3)2 + (y – 2)2
(x + 1)2 = (x – 3)2
x2 + 2x + 1 = x2 – 6x + 9
x2 + 2x + 6x – x2 = 9 – 1 = 8
8x = 8
x = 8/8 = 1
Now in right triangle ABC
AC2 = AB2 + BC2
(3 + 1)2 + (2 – 2)2 = (x + 1)2 + (y – 2)2 + (x – 3)2 + (y – 2)2
(4)2 + (0)2 = x2 + 2x + 1 + y2 – 4y + 4 + x2 – 6x + 9 + y2 – 4y + 4
16 = 2x2 + 2y2 – 4x – 8y + 18
2x2 + 2y2 – 4x – 8y = 16 – 18
2x2 + 2y2 – 4x – 8y = -2
x2 + y2 – 2x – 4y = -1 …….(i)
Now substitute the value of x, in eq(i), we get
(1)2 + y2 – 2 × 1 – 4y = -1
1 + y2 – 2 – 4y = -1
y2 – 4y = -1 – 1 + 2 = 0
y(y – 4) = 0
So the value of the y can be either y = 0
or y – 4 = 0, then y = 4
Hence, the coordinates of other points will be (1, 0) and (1, 4)
Share your thoughts in the comments
Please Login to comment...