Question 1. Find the centroid of the triangle whose vertices are:
(i) (1, 4), (-1, -1), and (3, -2)
Solution:
Given, vertices of triangle are (1, 4), (-1, -1), and (3, -2)
As we know that the coordinates of the centroid of a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3)
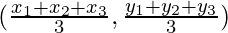
So, the coordinates of the centroid of a triangle are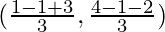
= (1, 1/3)
Hence, the centroid of the triangle whose vertices are (1, 4), (-1, -1), and (3, -2) is (1, 1/3).
(i) (-2, 3), (2, -1), and (4, 0)
Solution:
Given, vertices of triangle are (-2, 3), (2, -1), and (4, 0)
As we know that the coordinates of the centroid of a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3)
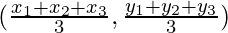
So, the coordinates of the centroid of a triangle are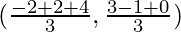
= (4/3, 2/3)
Hence, the centroid of the triangle whose vertices are (-2, 3), (2, -1), and (4, 0) is (4/3, 2/3).
Question 2. Two vertices of a triangle are(1, 2), (3, 5), and its centroid is at the origin. Find the coordinates of the third vertex.
Solution:
According to question
Two vertices of a triangle are(1, 2), (3, 5), and its centroid is at the origin
Find: the coordinates of the third vertex
So, let us assume that the coordinates of the third vertex is (x, y),
So, the coordinates of the centroid of a triangle are 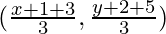
As we know that the centroid is at origin. So,
(x + 1 + 3)/3 = 0
x + 4 = 0
x = -4
(y + 2 + 5)/3 = 0
y + 7 = 0
y = -7
Hence, the third coordinate is (-4, -7)
Question 3. Find the third vertex of a triangle, If two of Its vertices are at (−3, 1) and (0, −2) and the centroid is at the origin.
Solution:
According to the question
ABC is a triangle in which the coordinates of A are (−3, 1), B are (0, −2), and C are (a, b)
and the centroid of the triangle ABC is (0, 0)
so,
(-3 + 0 + a)/3 = 0
a = 3
(1 – 2 + b)/3 = 0
b = 1
Hence, the coordinates of third vertex is (3, 1)
Question 4. A (3, 2) and B (−2, 1) are two vertices of a triangle ABC whose centroid G has the coordinates (5/3, -1/3). Find the coordinates of the third vertex C of the triangle.
Solution:
According to the question
ABC is a triangle in which the coordinates of A are (3, 2), B are (−2, 1), and C are (a, b)
and the centroid of the triangle ABC is (5/3, -1/3)
so,
(3 – 2 + a)/3 = 5/3
a = 4
(1 + 2 + b)/3 = -1/3
b = -4
Hence, the coordinates of third vertex is (4, -4)
Question 5. If (−2, 3), (4, −3), and (4, 5) are the mid-points of the sides of a triangle, Find the coordinates of Its centroid.
Solution:

Let us assume ABC is a triangle
Now in this triangle P, Q, R be the mid point of side, AC, AB, BC.
The coordinates of P(−2, 3), Q (4, −3), and R(4, 5)
Let us assume that the coordinates of A, B, and C are (x1, y1), (x2, y2), and (x3, y3)
As we know that P is the mid point of side AC,
So,
(x1 + x3) /2 = -2
= x1 + x3 = -4 …..(1)
(y1 + y3) /2 = 3
= y1 + y3 = 6 …..(2)
As we know that Q is the mid point of side AB,
So,
(x1 + x2) /2 = 4
= x1 + x2 = 8 …..(3)
(y1 + y2) /2 = -3
= y1 + y2 = -6 …..(4)
As we know that R is the mid point of side BC,
So,
(x2 + x3) /2 = 4
= x2 + x3 = 8 …..(5)
(y2 + y3) /2 = 5
= y2 + y3 = 10 …..(6)
Now add c
2(x1 + x2 + x3) = -4 + 8 + 8 = 12 …..( 7)
x1 + x2 + x3 = 6
Now subtract eq(1), (3), (5) from eq(7), we get
x1 = 10
x2 = -2
x3 = -2
Similarly, add (2), (4), and (6), we get
2(y1 + y2 + y3) = -6 + 6 + 10 = 10
y1 + y2 + y3 = 5 ……(8)
Now subtract eq(2), (4), (6) from eq(8), we get
y1 = -1
y2 = 11
y3 = -5
so, the coordinate of ABC triangle are (10, -1), (-2, 11), and (-2, -5)
Hence, the centroid of the triangle is ((10 – 2 – 2)/3, (-1 + 11 – 5)/3) = (2, 5/3)
Question 6. Prove analytically that the middle points of two sides of a triangle is equal to half to the third side.
Solution:

In triangle ABC,
D and E are the mid-points of the sides AB and AC
The DE = 1/2 BC
Let the coordinates of the vertices of a ∆ABC be (x1, y2), B(x2, y2), and C(x3, y3)
Then coordinates of D will be
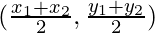
and coordinates of E will be
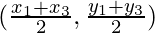
Length of BC=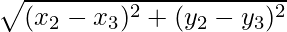 ……(1)
……(1)
and the length of DE
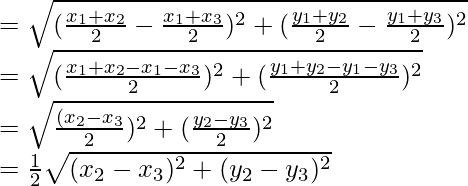
= 1/2 BC
Hence Proved
Question 7. Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the points of its diagonals meet in a point and bisect another.
Solution:

Let us assume the vertices of ABCD quadrilateral are A (x1, y1), B (x2, y2), C (x3, y3) and D (x4, y4)
In this quadrilateral, E and F are the mid-points of side BC and AD
and EF is joined G and H are the mid-points of diagonal AC and BD.
GH are joined
Now co-ordinates of E will be 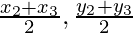
and co-ordinates of F will be 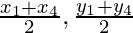
Co-ordinates of G will be 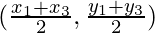
Co-ordinates of H will be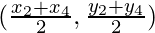
Here, EF and GH intersect each other at M.
So, let M is the midpoint of EF, then its coordinates will be
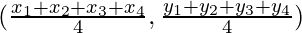
Let M is the midpoint of GH, then its coordinates of M will be
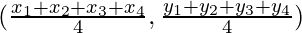
Here, we conclude that the coordinates of in both cases are same
Therefore, EF and GH bisect each other at M
Question 8. If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2 + PB2 + PC2 = GA2 + GB2 + GC2 + 3GP.
Solution:

According to the question
ABC is a triangle, G is the centroid of it let P(h, x) is any point in the plane.
We have to prove that PA2 + PB2 + PC2 = GA2 + GB2 + GC2 + 3GP
Proof:
In triangle ABC,
Let us assume the coordinates of are(x1, y1) of B are(x2, y2), and of C are(x3, y3)
Therefore, co-ordinates of centroid G will be (u, v)
Where u = (x1 + x2 + 3)/3 and v = (y1 + y2 + 3)/3
Now, we shall find L.H.S and R.H.S. separately
PA2 + PB2 + PC2 = (h – x1)2 + (k – y1)2 + (h – x2)2 + (k – y2)2 + (h – x3)2 + (k – y3)2
![Rendered by QuickLaTeX.com =3(h^2+k^2)+(x^2_1+x^2_2+x_3^2)+(y_1^2+y^2_2+y_3^2)-2h(x_1+x_2+x_3)-2k(y_1+y_2+y_3)\\ =3(h^2+k^2)+(x_1^2+x_2^2+x_3^2)+(y_1^2+y_2^2+y_3^2)-2h(3u)-2k(3v)\\ =3(h^2+k^2)-6hu-6kv+(x_1^2+x_2^2+x_3^2)+(x_1^2+x_2^2+x_3^2)GA^2+GB^2+GC^2+3GD^2\\ =(u-x_1)^2+(v-y_1)^2+(u-x_2)^2+(v-y_2)^2+(u-x_3)^2+(v-y_3)^2+3[(u-h)^2+(v-k)^2]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a506ae766ea9fb67f9fa2661db35f91e_l3.png)
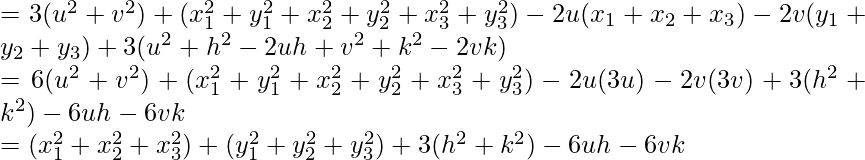
Hence proved
Question 9. If G be the centroid of triangle ABC, prove that AB2 + BC2 + CA2 = 3(GA2 + GB2 + GC2).
Solution:

According to the question
ABC is a triangle and G be the centroid of this triangle
We have to prove that AB2 + BC2 + CA2 = 3(GA2 + GB2 + GC2)
Proof:
Let us assume that the coordinates of the vertices of ∆ABC be
A(x1, y1), B(x2, y2), and C(x3, y3) and let G be the centroid of the triangle
Therefore, the coordinates of G will be
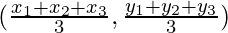
Now L.H.S.= AB2 + BC2 + CA2
= (x1 – x2)2 + (y1 – y2)2 + (x2 – x3)2 + (y2 – y3)2 + (x3 – x1)2 + (y3 – y1)2
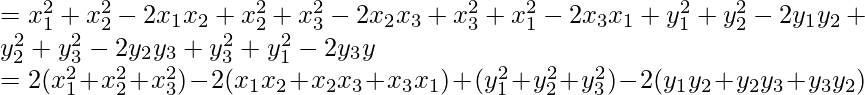
R.H.S = 3[GA2 + GB2 + GC2]
![Rendered by QuickLaTeX.com =3[(x_1-\frac{x_1+x_2+x_3}{3})^2+(y_1-\frac{y_1+y_2+y_3}{3})^2+(x_2-\frac{x_1+x_2+x_3}{3})^2+(y2-\frac{y_1+y_2+y_3}{3})^2+(x_3-\frac{x_1+x_2+x_3}{3})^3+(y_3-\frac{y_1+y_2+y_3}{3})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e56ac02a7f9617a2d11b837d2f289ac_l3.png)
![Rendered by QuickLaTeX.com =3[\frac{(2x_1-x_2-x_3}{3})^2+(\frac{2y_1+y_2-y_3}{3})^2+(\frac{2x_2-x_1-x_3}{3})^2+(\frac{2y_2-y_1-y_3}{3})^2+(\frac{2y_3-x_1-x_2}{3})^2+(\frac{2y_3-y_2-y_3}{3})^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1add7f91c8bf3975b46effe745e53b8e_l3.png)
![Rendered by QuickLaTeX.com =\frac{1}{3}[6x_1^2+6x_2^2-6x_1^2-6x_1x_2-6x_2x_3-6x_3x_1+6y_1^2+6y_2^2+6y_3^2-6y_1y_2-6y_2y_3-6y_3y_1]\\ =2[(x_1^2+x_2^2+x_3^2)-2(x_1x_2+x_2x_3+x_3x_1)+2(y_1^2+y_2^2+y_3^2+y_3^2+y_3^2)-2(y_1y_2+y_2y_3+y_3y_1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4aa5d894610c1d5c82be558d717007a4_l3.png)
= L.H.S
Hence proved
Question 10. In the figure, a right triangle BOA is given. C is the mid-point of the hypotenuse AB. Show that it is equidistant from the vertices O, A, and B.

Solution:
In right triangle OAB,
Co-ordinates of O are (0, 0), A are(2a, 0), and of B are(0, 2b)
C is the midpoint of AB. So, the co-ordinates of C will be
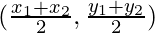
or
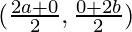
Now CO = 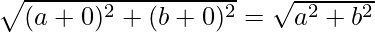
CA = 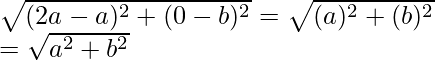
CB = 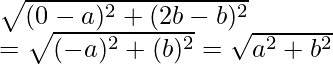
So, we can conclude that, CO = CA = CB
Hence, C is equidistant to form the vertices O, A and B.
Hence proved
Share your thoughts in the comments
Please Login to comment...