Question 1. Find the area of a triangle whose vertices are:
(i) (6, 3), (-3, 5) and (4, -2)
Solution:
Let us assume ABC is a triangle whose vertices are A(6, 3), B(-3, 5) and C(4, -2)
So,
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[6(5 + 2) + (-3)(-2 – 3) + 4(3 – 5)]
= 1/2[6(5 + 2) + (-3)(-2 – 3) + 4(3 – 5)]
= 1/2[42 + 15 – 8]
= 1/2 * 49
= 49/2 sq.unit
(ii) (at12, 2at1), (at22, 2at2) and (at32, 2at3)
Solution:
Let us assume ABC is a triangle whose vertices are A(at12, 2at1), (at22, 2at2) and (at32, 2at3)
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[at12(2at2 – 2at3) + at22(2at3 – 2at1) + at32(2at1 – 2at2)]
= 1/2[at122at2 – at122at3 + at222at3 – at222at1 + at322at1 – at322at2]
= 1/2 × 2a2[t12t2 – t12t3 + t22t3 – t22t1 + t32t1 – t32t2]
= a2[t12(t2 – t3) + t22(t3 – t1) + t32(t1 – t2)]
(iii) (a, c + a), (a, c) and (-a, c – a)
Let us assume ABC is a triangle whose vertices are A(a, c + a), B(a, c) and C(-a, c – a)
So, Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[a(c – c + a)a(c – a – c – a) + (-a)(c + a – c)]
= 1/2(a2 – 2a2 – a2)
= 1/2(-2a2)
= a2sq.units
Question 2. Find the area of the quadrilaterals, the coordinates of whose vertices are
(i) (-3, 2), (5, 4), (7, -6) and (-5, -4)
Solution:

Let us considered ABCD is a quadrilateral whose vertices are A(-3, 2), B(5, 4), C(7, -6) and D(-5, -4)
So, Area of ABCD = Area of ∆ABC + Area of ∆ADC ….(1)
So,
So, Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [-3(4 + 6) + (-6 – 2) + 7(2 – 4)]
= 1/2 [-3(10) + 5 * (-8) + 7 * (-2)]
= 1/2 [-30 – 40 – 14]
= 1/2 [-30-40-14]
= 1/2 (-84)
= -42
= 42 sq.units (Area cannot be in negative)
Similarly, area of ∆ADC
= 1/2 [-3(-6 + 4) + 7(-4 – 2) + (-5)(2 + 6)]
= 1/2 [-3(-2) + 7(-6) + (-5)(8)]
= 1/2 [6 – 42 – 40]
= 1/2 (-76)
= -38
= 38 sq. Units(Area cannot be in negative)
Now put all these values in eq(1), we get
Area of quadrilateral ABCD = 42 + 38 = 80 sq.units
(ii) (1, 2), (6, 2), (5, 3) and (3, 4)
Solution:

Let us considered ABCD is a quadrilateral whose vertices are A(1, 2), B(6, 2), C(5, 3) and D(3, 4)
So, Area of ABCD = Area of ∆ABC + Area of ∆ADC ….(1)
So, Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [1(2 – 3) + 6(3 – 2) + 5(2 – 2)]
= 1/2[-1 + 6 + 0]
= 1/2 (5)
= 5/2 sq.units
Similarly, area of ∆ADC
= 1/2 [1(3 – 4) + 5(4 – 2) + 3(2 – 3)]
= 1/2 [1 * (-1) + 5 * 2 + 3 * (-1)]
= 1/2 [-1 + 10 – 3]
= 1/2 * 6
= 3 sq.units
Now put all these values in eq(1), we get
Area of quadrilateral ABCD = 5/2 + 3 = (5 + 6)/2 = 11/2 sq.units
(iii) (-4, -2), (-3, -5), (3, -2), (2, 3)
Solution:

Let us considered ABCD is a quadrilateral whose vertices are A(-4, -2), B(-3, -5), C(3, -2), D(2, 3)
So, Area of ABCD = Area of ∆ABC + Area of ∆ADC ….(1)
So, Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [-4(-5 + 2) – 3(-2 + 2) + 3(-2 + 5)]
= 1/2 [-4 * (-3) – 3 * 0 + 3 * 3]
= 1/2 [12 + 0 + 9]
= 1/2 * 21
= 21/2 sq.units
Similarly, area of ∆ADC,
= 1/2 [-4(-2 – 3) + 3(3 + 2) + 2(-2 + 2)]
= 1/2[-4 * (-5) + 3 * 5 + 2 * 0]
= 1/2 [20 + 15 + 0]
= 1/2 * 35
= 35/2 sq.units
Now put all these values in eq(1), we get
Area of quadrilateral ABCD = 21/2 + 35/2 + 56/2 = 28 sq.units
Question 3. The four vertices of a quadrilateral are (1, 2), (-5, 6), (7, -4) and (k, -2) taken in order. If the area of the quadrilateral is zero, find the value of k?
Solution:

Let us considered ABCD is a quadrilateral whose vertices are A(1, 2), B(-5, 6), C(7, -4) and D(k, -2)
So, Area of ABCD = Area of ∆ABC + Area of ∆ADC ….(1)
Now area of ∆ABC
= 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [1(6 + 4) + (-5)(-4 – 2) + 7(2 – 6)]
= 1/2 [1 * 10 + (-5)(-6) + 7(-4)]
= 1/2 [10 + 30 – 28]
= 1/2 × 12
= 6sq.units
Similarly, area of ∆ADC,
= 1/2 [1(-4 + 2) + 7(-2 – 2) + k(2 + 4)]
= 1/2 [1(-2) + 7(-4) + k(-4)]
= 1/2 [-2 – 28 + 6k]
= 1/2 (-30 + 6k)
= -15+3k
= 3k – 15 sq.units
Now put all these values in eq(1), we get
Area of quadrilateral ABCD = 6 + 3k – 15
But it is given that the area of quadrilateral ABCD = 0
So,
0 = 6 + 3k – 15
k = 9/3 = 3
Hence, the value of k is 3.
Question 4. The vertices of ∆ABC are (-2, 1), (5, 4), and (2, -3) respectively. Find the area of the triangle and the length of the altitude through A.
Solution:

Given that, ABC is a triangle whose vertices are A(-2, 1), B(5, 4), and C(2, -3)
and AD ⊥ BC, let us assume AD = h
So, area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [-2(4 + 3) + 5(-3 – 1) + 2(1 – 4)]
= 1/2 [-2 * 7 + 5 * (-4) + 2(-3)]
= 1/2[-14 – 20 – 6]
= 1/2 * (-40)
= -20
= 20 sq. units
Now we find the length of BC = 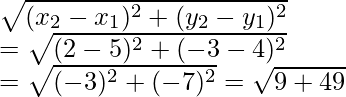
= √58 units
So, the area of ∆ABC = 1/2 * base * height
⇒ 20 = 1/2 * 58 * h
⇒ h = (20 * 2)/√58 = 40/√58 units
Question 5. Show that the following sets of points are collinear
(i) (2, 5), (4, 6) and (8, 8)
Solution:
As we know that 3 points are collinear is the area of the triangle formed by them is zero
So, let us assume ABC is a triangle whose vertices A(2, 5), B(4, 6) and C(8, 8)
So, area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[2(6 – 8 + 4(8 – 5) + 8(5 – 6)]
= 1/2 [2 * (-2) + 4 * 3 + 8 * (-1)]
= 1/2 [-4 + 12 – 8]
= 1/2 * 0 = 0
Area of ∆ABC = 0
Hence, points A, B and C are collinear
Hence proved
(b) (1, -1), (2, 1) and (4, 5)
Solution:
As we know that 3 points are collinear is the area of the triangle formed by them is zero
So, let us assume ABC is a triangle whose vertices A(1, -1), B(2, 1) and C(4, 5)
So, area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [1(1 – 5) + 2(5 + 1) + 4(-1 – 1)]
= 1/2 [1(-4) + 2 * 6 + 4(-2)]
= 1/2 [-4 + 12 – 8]
= 1/2 * 0 = 0
Area of ∆ABC = 0
Hence, points A, B and C are collinear
Hence proved
Question 6. Find the area of a quadrilateral ABCD, the coordinates of whose vertices are A (-3, 2), B (5, 4), C (7, -6), and D (-5, -4).
Solution:
Given that, ABCD is a quadrilateral whose vertices A (-3, 2), B (5, 4), C (7, -6), and D (-5, -4).
So, Area of quadrilateral ABCD = area of ∆ABC + area of ∆ACD
= 1/2|(-12 – 30 + 14) – (10 + 28 + 18)| + 1/2|(18 – 28 – 10) – (14 + 30 + 12)|
= 1/2|-28 – 56| + 1/2|-20 – 56|
= 1/2|-84| + 1/2|-76|
= 42 + 38
= 80 sq.units
Hence, the area of quadrilateral is 80 sq.units
Question 7. In ∆ABC, the coordinates of vertex A are (0, -1) and D (1, 0) and E (0, 1) respectively the mid-points of the sides AB and AC. If F is the mid-point of side C, find the area of ∆DEF.
Solution:

Given that ∆ABC, the coordinates of vertex A are (0, -1) and D (1, 0) and E (0, 1) are
the mid points of the sides AB and AC
Let us considered B (p, q), C (r, s) and F (x, y)
So, Mid-point of AB = Coordinates of D
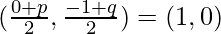
p/2 = 1
p = 2
Therefore, B(p, q) = B(2, 1)
(-1 + q)/2 = 0
-1 + q = 0
q = 1
Mid-point of AC = coordinates of E
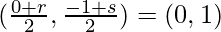
r/2 = 0
r = 0
(-1 + s)/2 = 1
-1 + s = 2
s = 3
Now, C(r, s) = C(0, 3)
Coordinates of F = Midpoint of BC
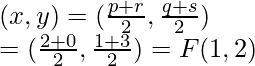
So, the coordinates of A(0,-1), B(2, 1) and C(0, 3)
Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [0(1 – 3) + 2(3 + 1) + 0(-1 – 1)]
= 1/2(8) = 4sq.units
And the coordinate of D(1, 0), E(0, 1), and F(1, 2)
Area of ∆DEF = 1/2[1(1 – 2) + 0(2 – 0) + 1(0 – 1)]
= 1/2(-1 – 1) = -1
= 1 sq.unit (Area cannot be in negative)
Question 8. Find the area of the triangle PQR with Q (3, 2) and the mid-points of the sides through Q being (2, -1) and (1, 2).
Solution:
Given that, ∆PQR, L and N are mid-points of QR and QP, and the coordinates of Q are (3, 2) of L are (2, -1) and of N are (1, 2)
Let us assume that the coordinates of R be (x1, y1) and P(x2,y2)
2 = (3 + x1)/2 ⇒ 3 + x1 = 4 ⇒ x1 = 4 – 3 = 1
and -1 = (2 + y)/2 ⇒ -2 = 2 + y ⇒ y = -2 – 2 = -4
The coordinates of R are (1,-4)
Similarly coordinates of P will be
1 = (3 + x1)/2 ⇒ 3 + x1 = 2 ⇒ x1 = 2 – 3 = -1
and (2 + y)/1 = 2 ⇒ 2 + y = 4 ⇒ y = 4 – 2 = 2
Coordinates of P are (-1, 2)
Now area of ∆PQR
= 1/2 [(-12 + 2 – 2) – (2 + 4 + 6)]
= 1/2[-12 – 12] = -12
= 12 sq.units
Question 9. If P (-5, -3), Q (-4, -6), R (2, -3) and S (1, 2) are the vertices of a quadrilateral PQRS, find its area.
Solution:
Given that, PQRS quadrilateral whose vertices are P (-5, -3), Q (-4, -6), R (2, -3) and S (1, 2)
Area of PQRS quadrilateral = Area of ∆PQR + Area of ∆PSR ….(1)
Now area of ∆PQR = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[-5(-6 + 3) + (-4)(-3 + 3) + 2(-3 + 6)]
= 1/2[-5 * (-3) + (-4 * 0) + 2 * 3]
= 1/2(15 + 0 + 6)
= 1/2 * 21
= 21/2
Similarly the area ∆PSR,
= 1/2[-5 * (2 + 3) + 1(-3 + 3) + 2(-3 – 2)]
= 1/2[-5 * 5 + 1 * 0 + 2 * (-5)]
= 1/2[-25 + 0 – 10]
= 1/2 * (-35)
= -35/2
Now put all these values in eq(1), we get
Area of quadrilateral PQRS = 21/2 + (-35/2) = 28 sq.unit
Question 10. If A (-3, 5), B (-2, -7), C (1, -8), and D (6, 3) are the vertices of a quadrilateral ABCD, find its area.
Solution:
Let us considered ABCD is a quadrilateral whose vertices areA (-3, 5), B (-2, -7), C (1, -8), and D (6, 3)
So, Area of ABCD = Area of ∆ABC + Area of ∆ACD ….(1)
So, Area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2 [-3(-7 + 8) + (-2)(-8 – 5) + 1(5 + 7)]
= 1/2 [-3 * 1 + 26 + 12]
= 1/2[-3 + 26 + 12]
= 35/2 sq.units
Similarly, area of ∆ACD = 1/2[-3(-8 – 3) + 1(3 – 5) + 6(5 + 8)]
= 1/2 [-3 * (-11) + 1(-2) + 6 * 13]
= 1/2[33 – 2 + 78]
= 1/2 * 109
= 109/2 sq.units
Now put all these values in eq(1), we get
Area of quadrilateral ABCD = 35/2 + 109/2 = 144/2 = 72 sq.units
Question 11. For what value of ‘a’ the points (a, 1), (1, -1), and (11, 4) are collinear?
Solution:
Let us assume the vertices of ∆ABC are A (a, 1), B (1, -1) and C (11, 4)
Now area of ∆ABC = 1/2[x1(y2 – y3) + (y3 – y1)x2 + x3(y1 – y2)]
= 1/2[a(-1 – 4) + 1(4 – 1) + 11(1 + 1)]
= 1/2[-5a + 3 + 22]
= 1/2(25 – 5a)
It is given that the points A,B an C are collinear
so, area of ∆ABC = 0
1/2 (25 – 5a) = 0
⇒ 25 – 5a = 0
⇒ a = 25/5 = 5
Hence, the value of a is 5
Share your thoughts in the comments
Please Login to comment...