Class 11 RD Sharma Solutions – Chapter 25 Parabola – Exercise 25.2

Question 1. Find the axis of symmetry of the parabola y² = x. 

Solution:

We are given,

=> y² = x

We know this parabola lies on the y-axis. 

Therefore, its vertex lies on the y-axis.

Now we know, parabola always has one axis which maintains its symmetry.

In this case, the axis is an x-axis, which divides the parabola into two equal parts.

Hence the required axis is x-axis. 

Question 2. Find the distance between the vertex and the focus of the parabola y² + 6y + 2x + 5 = 0.

Solution:

Given that,  

y² + 6y + 2x + 5 = 0  

(y + 3)² + 2x – 4 = 0

(y + 3)² = -2 (x – 2)

Let us assume Y = y + 3 and X = x – 2.

From the equation, we get,

Y² = – 2X

On putting 4a = 2, we get

=> a = 1/2

Focus = (X = -1/2, Y = 0) = (x = 3/2, y = -3)

Vertex = (X = 0, Y = 0) = (x = 2, y = -3)

Thus, we get

Focus = (3/2, -3)

Vertex = (2, -3)

The distance between the vertex and the focus is,

D =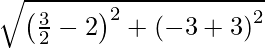 

= 

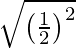
= 1/2 units

Therefore, the required distance is 1/2 units.

Question 3. Find the equation of the directrix of the parabola x² − 4x − 8y + 12 = 0.

Solution:

Given that,

x² − 4x − 8y + 12 = 0  

(x – 2)² – 4 – 8y + 12 = 0

(x – 2)² = 8 (y – 1)

Let Y = y − 1 and X = x – 2.

From the above equation, we get,

X² = 8Y

On comparing with x² = 4ay, we get

=> a = 2

Directrix = Y = −a

=> y − 1 = −a

=> y = −a + 1

=> y = −2 + 1

=> y = −1  

Therefore, the equation of the directrix is y = -1.

Question 4. Write the equation of the parabola with focus (0, 0) and directrix x + y − 4 = 0.

Solution:

Let us assume P (x, y) be any point on the parabola whose focus is S (0, 0).

And the equation of directrix is x + y= 4.  

First we draw PM perpendicular to x + y = 4.

Then, we have,

SP = PM

SP² = PM²

(x – 0)² + (y – 0)² =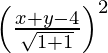 

x² + y² =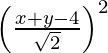 

2x² + 2y² = x² + y² + 16 + 2xy – 8y – 8x

=> x² + y² – 2xy + 8x + 8y – 16 = 0

Hence, the equation of the parabola is x² + y² – 2xy + 8x + 8y – 16 = 0

Question 5. Find the length of the chord of the parabola y² = 4ax which passes through the vertex and is inclined to the axis at π/4.

Solution:

Let us considered OP be the chord and the coordinates of P be (x₁, y₁).

We have,

=> OP² = x₁² + y₁²

And, tan π/4 = y₁/x₁

=> 1 = y₁/x₁

=> x₁ = y₁

and (x₁, y₁) lies on the parabola.  

∴ y₁² = 4ax₁

So, we get

=> x₁² = 4a x₁ 

=> x₁ = 4a

Therefore, we have 

OP² = (4a)² + (4a)²

OP² = 32a²

OP = 4√2 a

Therefore, the length of the chord is 4√2 a.

Question 6. If b and c are the lengths of the segments of any focal chord of the parabola y² = 4ax, then write the length of its latus-rectum.

Solution:

Let us assume S (a, 0) be the focus of the given parabola and the end points of the focal chord be P(at² , 2at) and Q (a/t²}, -2a/t).

Now, SP and SQ are segments of the focal chord with lengths b and c.

∴ SP = b, SQ = c  

Also, SP =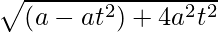 

= a (1 + t²)

And, SQ =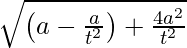 

= a (1 + 1/t²)

Now, we get,

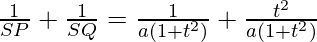
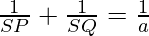
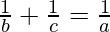
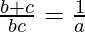
=> a =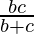 

Hence, the length of the latus rectum is 4a =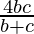 

Question 7. PSQ is a focal chord of the parabola y² = 8x. If SP = 6, then find SQ. 

Solution:

According to the question, it is given that PSQ is a focal chord of the parabola y² = 8x and SP = 6

So, the coordinates of the focal chord are P (at² , 2at) and Q (a/t², – 2a/t).

On comparing y² = 8x with y² = 4ax, we get, 

=> 4a = 8

=> a = 2  

Therefore, the coordinates of the focus S is (2, 0).

SP = 6  

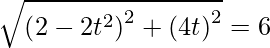
t⁴ + 2t² – 8 = 0

=> t² = 2

Thus, we get,

SQ =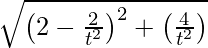 

= 

= 

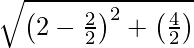
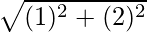
= √5

Hence, SQ is √5.

Question 8. Write the coordinates of the vertex of the parabola whose focus is at (−2, 1) and directrix is the line x + y − 3 = 0.

Solution:

Given that, the focus S is at (−2, 1) and the directrix is the line x + y − 3 = 0 and the slope of the line perpendicular to x + y − 3 = 0 is 1.

Now, the axis of the parabola is perpendicular to the directrix and passes through the focus.

So, the equation of the axis of the parabola becomes,

=> y – 1 = 1 (x + 2)

Now, the intersection point of the directrix and axis is the intersection point of parabola and x + y − 3 = 0.

Let us assume that the intersection point be  K.

So, the coordinates of K are (0, 3).

Let us assume that the point (h, k) be the coordinates of the vertex, which is the mid-point of the line segment joining K and the focus.

=> h = (0 – 2)/2, k = (3 + 1)/2

=> h = -1, k = 2

Hence, the coordinates of the vertex are (−1, 2).

Question 9. If the coordinates of the vertex and focus of a parabola are (−1, 1) and (2, 3) respectively, then write the equation of its directrix. 

Solution:

Given that, the vertex and the focus of a parabola are (−1, 1) and (2, 3).

So, the slope of the axis of the parabola = 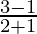 = 2/3

Slope of the directrix = -3/2

Let us assume the directrix intersect the axis at point K (r, s).  

So, (r + 2)/2 = -1, (s + 3)/2 = 1

=> r = -4, s = -1

Now, the required equation of the directrix is,

y + 1 = (-3/2) (x + 4)

=> 3x + 2y + 14 = 0

Question 10. If the parabola y² = 4ax passes through the point (3, 2), then find the length of its latus rectum. 

Solution:

Given that, y² = 4ax and the parabola is passing through the point (3, 2)

So, this will satisfy the equation of the parabola.

22 = 4(a)(3)  

=> a = 1/3

The length of the latus rectum = 4a

= 4 (1/3)

= 4/3

Hence, the latus rectum is 4/3

Question 11. Write the equation of the parabola whose vertex is at (−3, 0) and the directrix is x + 5 = 0. 

Solution:

Given that the vertex(h, k) is (-3, 0) and the directrix is x + 5 = 0

So, the general equation of the parabola = (y − k)² = 4a (x − h).

Now, the directrix is 

x = h − a

As x + 5 = 0, we get

=> −5 = −3 − a                          

=> a = 2

So, the equation of the parabola is 

(y − 0)² = 4 (2) (x + 3)

=> y² = 8 (x + 3)