Class 12 RD Sharma Solutions – Chapter 31 Probability – Exercise 31.7 | Set 2
Last Updated :
21 Jul, 2021
Question 14. An item is manufactured by three machines A, B, and C. Out of the total number of items manufactured during a specified period, 50% are manufactured on machine A, 30% on Band 20% on C. 2% of the items produced on A and 2% of items produced on B are defective and 3% of these produced on C are defective. All the items are stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
Solution:
Let us assume that E be the event of getting a defective item.
So, we have
P(A) = 50 % = 1/2
P(B) = 30 % = 3/10
P(C) = 20 % = 1/5
Also we have,
P(E/A) = 2 % = 1/50
P(E/B) = 2 % = 1/50
P(E/C) = 3 % = 3/100
Now,
P(the defective item drawn was manufactured on machine A) = 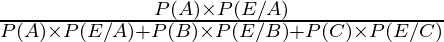
= 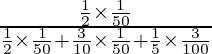
= 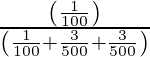
= 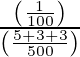
= 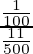
= 500/1100
= 5/11
Question 15. There are three coins. One is a two-headed coin (having a head on both faces), another is a biased coin that comes up heads 75% of the time and the third is also a biased coin that comes up tail 40% of the time. One of the three coins is chosen at random and tossed, and it shows heads. What is the probability that it was the two-headed coin?
Solution:
Let us assume
A = the event of choosing two-headed coin,
B = the event of choosing a biased coin that comes up head 75 % of the times
C = the event of choosing a biased coin that comes up tail 40 % of the times
E = the event of getting a head.
Now,
P(A) = 1/3
P(B) = 1/3
P(B) = 1/3
Also we have,
P(E/A) = 1
P(E/B) = 75 % = 75/100 = 3/4
P(E/C) = 60 % = 60/100 = 3/5
By using Bayes’ theorem, the required probability is
P(the head shown was of two-headed coin) = P (A/E)
= 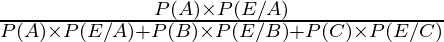
= 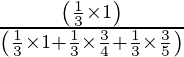
= 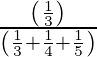
= 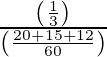
= 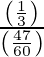
= 20/47
Question 16. In a factory, a machine A produces 30% of the total output, machine B produces 25%, and machine C produces the remaining output. If defective items produced by machines A, B, and C are 1%, 1.2%, 2% respectively. Three machines working together produce 10000 items in a day. An item is drawn at random from a day’s output and found to be defective. Find the probability that it was produced by machine B?
Solution:
Let us assume that the events are
A = the item is defective
E1 = machine A is chosen
E2 = machine B is chosen
E3 = machine C is chosen
So,
P(E1) = 30/100
P(E2) = 25/100
P(E3) = 45/100
Now,
P(A/E1) = 1/100
P(A/E2) = 1.2/1000
P(A/E3) = 2/100
By using Bayes’ theorem, the required probability is
P(E1/A) = 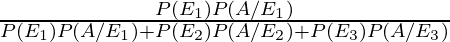
= 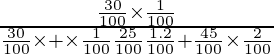
= 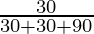
= 30/150
= 1/5
= 0.2
Question 17. A company has two plants to manufacture bicycles. The first plant manufactures 60% of the bicycles and the second plant 40%. Out of the 80% of the bicycles are rated of standard quality at the first plant and 90% of standard quality at the second plant. A bicycle is picked up at random and found to be of standard quality. Find the probability that it comes from the second plant.
Solution:
Let us assume that the events are
A = the cycle is of standard quality
E1 = plant I is chosen
E2 = plant II is chosen.
So,
P(E1) = 60/100
P(E2) = 40/100
Now,
P(A/E1) = 80/100
P(A/E2) = 90/100
By using Bayes’ theorem, the required probability is
P(E2/A) = 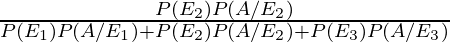
= 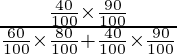
= 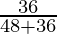
= 36/84
= 3/7
Question 18. Three urns A, B, and C contain 6 red and 4 white; 2 red and 6 white; and 1 red and 5 white balls respectively. An urn is chosen at random and a ball is drawn. If the ball drawn is found to be red, find the probability that the ball was drawn from urn A.
Solution:
Let us assume that the events are
A = the ball is red
E1 = urn A is chosen
E2 = urn B is chosen
E2 = urn C is chosen.
So, P(E1) = 1/3
P(E2) = 1/3
P(E3) = 1/3
Now,
P(A/E1) = 6/10 = 3/5
P(A/E2) = 2/8 = 1/4
P(A/E3) = 1/6
By using Bayes’ theorem, the required probability is
P(E1/A) = 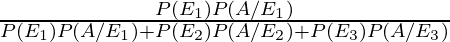
= 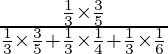
= 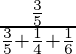
= 36/61
Question 19. In a group of 400 people, 160 are smokers and non-vegetarian, 100 are smokers and vegetarian and the remaining are non-smokers and vegetarian. The probabilities of getting a special chest disease are 35%, 20%, and 10% respectively. A person is chosen from the group at random and is found to be suffering from the disease. What is the probability that the selected person is a smoker and non-vegetarian?
Solution:
Let us assume that the events are
A = the person suffers from the disease
E1 = a smoker and a non-vegetarian
E2 = a smoker and a vegetarian
E3 = a non-smoker and a vegetarian
So, P(E1) = 160/400
P(E2) = 100/400
P(E3) = 140/400
Now,
P(A/E1) = 35/100
P(A/E2) = 20/100
P(A/E3) = 10/100
By using Bayes’ theorem, the required probability is
P(E1/A) = 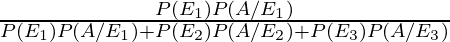
= 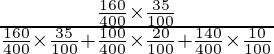
= 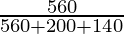
= 560/900
= 28/45
Question 20. A factory has three machines A, B, and C, which produce 100, 200, and 300 items of a particular type daily. The machines produce 2%, 3% and 5% defective items respectively. One day when the production was over, an item was picked up randomly and it was found to be defective. Find the probability that it was produced by machine A.
Solution:
Let us assume that the events are
A = the item is defective
E1 = machine A is chosen
E2 = machine B is chosen
E3 = machine C is chosen
So, P(E1) = 100/600
P(E2) = 200/600
P(E3) = 300/600
Now,
P(A/E1) = 2/100
P(A/E2) = 3/100
P(A/E3) = 5/100
By using Bayes’ theorem, the required probability is
P(E1/A) = 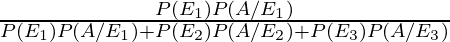
= 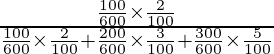
= 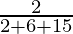
= 2/23
Question 21. A bag contains 1 white and 6 red balls, and a second bag contains 4 white and 3 red balls. One of the bags is picked up at random and a ball is randomly drawn from it and is found to be white in color. Find the probability that the drawn ball was from the first bag.
Solution:
Let us assume the events are
A = the ball is white
E1 = bag I is chosen
E2 = bag II is chosen
So, P(E1) = 1/2
P(E2) = 1/2
Now,
P(A/E1) = 1/7
P(A/E2) = 4/7
By using Bayes’ theorem, the required probability is
P(E1/A) = 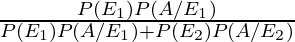
= 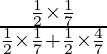
= 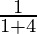
= 1/5
Question 22. In a certain college, 4% of boys and 1% of girls are taller than 1.75 meters. Furthermore, 60% of the students in the colleges are girls. A student selected at random from the college is found to be taller than 1.75 meters. Find the probability that the selected student is a girl.
Solution:
Let us assume the events are
A = The height of the student is more than 1.75 m
E1 = The selected student is a girl
E2 = The selected student is a boy
So,
P(E1) = 60/100
P(E2) = 40/100
Now,
P(A/E1) = 1/100
P(A/E1) = 4/100
By using Bayes’ theorem, the required probability is
P(E1/A) = 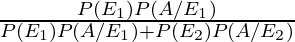
= 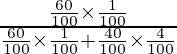
= 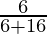
= 6/22
= 3/11
Question 23. For A, B, and C the chances of being selected as the manager of a firm are in the ratio 4:1:2 respectively. The respective probabilities for them to introduce a radical change in marketing strategy are 0.3, 0.8, and 0.5. If the change does take place, find the probability that it is due to the appointment of B or C.
Solution:
Let us assume the events are
A = The change takes place
E1 = A is selected
E2 = B is selected
E3 = C is selected
So,
P(E1) = 4/7
P(E2) = 1/7
P(E3) = 2/7
Now,
P(A/E1) = 0.3
P(A/E2) = 0.8
P(A/E3) = 0.5
By using Bayes’ theorem, the required probability is
P(E1/A) = 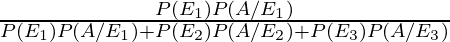
= 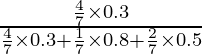
= 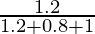
= 1.2/3
= 2/5
1 – P(E1/A) = 1 – 2/5 = 3/5
Question 24. Three persons A, B, and C apply for a job of Manager in a Private Company. Chances of their selection (A, B, and C) are in the ratio 1 : 2 : 4. The probabilities that A, B, and C can introduce changes to improve the profits of the company are 0.8, 0.5, and 0.3, respectively. If the change does not take place, find the probability that it is due to the appointment of C.
Solution:
Let us assume the events are
E1 = The selection of A as manager
E2 = The selection of B as manager
E3 = The selection of C as manager
So,
P(E1) = The probability of selection of A = 1/7
P(E2) = The probability of selection of B = 2/7
P(E3) = The probability of selection of C = 4/7
Let us assume that A be the event representing the change not taking place.
P(A/E1) = Probability that A does not introduce change = 0.2
P(A/E2) = Probability that B does not introduce change = 0.5
P(A/E3) = Probability that C does not introduce change = 0.7
So, the required probability = P(A/E3)
By using Bayes’ theorem, the required probability is
P(A/E3) = 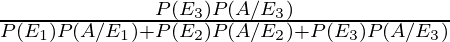
= 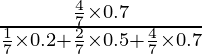
= 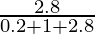
= 2.8/4
= 0.7
Question 25. An insurance company insured 2000 scooters and 3000 motorcycles. The probability of an accident involving a scooter is 0.01 and that of a motorcycle is 0.02. An insured vehicle met with an accident. Find the probability that the accident vehicle was a motorcycle.
Solution:
Let us assume the events are
A = The vehicle meets the accident
E1 = is a scooter
E2 = is a motorcycle
So,
P(E1) = 2000/5000 = 0.4
P(E2) = 3000/5000 = 0.6
Now,
P(A/E1) = 0.01
P(A/E2) = 0.02
By using Bayes’ theorem, the required probability is
P(E2/A) = 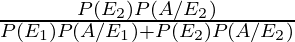
= 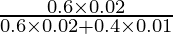
= 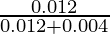
= 0.012/0.016
= 3/4
Question 26. Of the students in a college, it is known that 60% reside in a hostel and 40% do not reside in a hostel. Previous year results report that 30% of students residing in hostel attain A grade and 20% of ones not residing in hostel attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade. What is the probability that the selected student is a hosteler?
Solution:
Let us assume the events are
A = The selected student attains grade A
E1 = resides in a hostel
E2 = does not reside in a hostel
So, P(E1) = 60/100
P(E2) = 40/100
Now,
P(A/E1) = 30/100
P(A/E2) = 20/100
By using Bayes’ theorem, the required probability is
P(E1/A) = 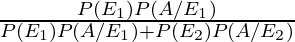
= 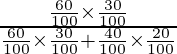
= 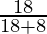
= 9/13
Share your thoughts in the comments
Please Login to comment...