Class 12 RD Sharma Solutions – Chapter 18 Maxima and Minima – Exercise 18.2

Read

Discuss

Find the points of local maxima or local minima, if any, of the following functions, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be:

Question 1. f(x) = (x – 5)⁴

Solution:

Given function

f(x) = (x – 5)⁴

Now, differentiate the given function w.r.t. x

f ‘(x) = 4(x-5)³

Now, for local maxima and minima

Put f ‘(x) = 0

⇒ 4(x – 5)³= 0

⇒ x – 5 = 0

⇒ x = 5

So, at x = 5, f'(x) changes from negative to positive. Hence, x = 5 is the point of local minima

So, the minimum value is f(5) = (5 – 5)⁴ = 0

Question 2. f(x) = x³– 3x

Solution:

Given function

f(x) = x³– 3x

Now, differentiate the given function w.r.t. x

f ‘(x) = 3x²– 3

Now, for local maxima and minima

Put f ‘(x) = 0

⇒ 3x²– 3 = 0

⇒ x = ±1

Now, again differentiating f'(x) function w.r.t. x

f “(x) = 6x

Put x = 1 in f”(x)

f “(1)= 6 > 0

So, x = 1 is point of local minima

Put x = -1 in f”(x)

f “(-1)= -6 < 0

So, x = -1 is point of local maxima

So, the minimum value is f(1) = x³– 3x = 1³– 3 = -2

and the maximum value is f(-1) = x³– 3x = (-1)³ – 3(-1) = 2

Question 3. f(x) = x³(x – 1)²

Solution:

Given function

f(x) = x³(x – 1)²

Now, differentiate the given function w.r.t. x

f ‘(x) = 3x² (x- 1)² + 2x³(x- 1)

= (x – 1) (3x²(x – 1) + 2x³)

= (x – 1) (3x³ – 3x² + 2x³)

= (x – 1) (5x³ – 3x²)

= x²(x – 1) (5x – 3)

Now, for all maxima and minima,

Put f ‘(x) = 0

= x²(x – 1) (5x- 3) = 0

x = 0, 1, 3/5

So, at x = 3/5, f'(x) changes from negative to positive. Hence, x = 3/5 is a point of minima

So, the minimum value is f(3/5) = (3/5)³(3/5 – 1)²= 108/3125

At x = 1, f'(x) changes from positive to negative. Hence, x = 1 is point of maxima.

So, the maximum value is f(1) = (1)³(1 – 1)²= 0

Question 4. f (x) = (x – 1) (x + 2)²

Solution:

Given function

f(x) = (x – 1)(x + 2)²

Now, differentiate the given function w.r.t. x

f ‘(x) = (x + 2)² + 2(x – 1)(x + 2)

= (x+ 2) (x+ 2 + 2x – 2)

=(x + 2) (3x)

Now, for all maxima and minima,

Put f ‘(x) = 0

⇒ (x + 2) (3x) = 0

x = 0,-2

So, at x = -2, f(x) changes from positive to negative. Hence, x = -2 is a point of Maxima

So, the maximum value is f(-2) = (-2 – 1)(-2 + 2)²= 0

At x = 0, f ‘(x) changes from negative to positive. Hence, x = 0 is point of Minima.

So, the minimum value is f(0) = (0 – 1)(0 + 2)²= -4

Question 5. f(x) = (x – 1)³(x + 1)²

Solution:

Given function

f(x) = (x – 1)³ (x + 1)²

Now, differentiate the given function w.r.t. x

f ‘(x) = 3(x – 1)² (x + 1)² + 2(x – 1)³ (x + 1)

= (x – 1)² (x + 1) {3(x + 1) + 2(x – 1)}

= (x – 1)² (x + 1) (5x + 1)

Now, for local maxima and minima,

Put f ‘(x) = 0

⇒ (x – 1)² (x + 1) (5x + 1) = 0

⇒ x = 1, -1, -1/5

So, at x = -1, f ‘(x) changes from positive to negative. Hence, x = -1 is point of maxima

So, the maximum value is f(-1) = (-1 – 1)³ (-1 + 1)²= 0

At x = -1/5, f ‘(x) changes from negative to positive so x= -1/5 is point of minima

So, the minimum value is f(-1/5) = (-1/5 – 1)³ (-1/5 + 1)²= -3456/3125

Question 6. f(x) = x³ – 6x² + 9x +15

Solution:

Given function

f(x) = x³ – 6x² + 9x + 15

Now, differentiate the given function w.r.t. x

f ‘(x) = 3x² – 12x + 9

= 3 (x²– 4x + 3)

= 3 (x – 3) (x – 1)

Now, for local maxima and minima,

Put f ‘(x) = 0

⇒ 3 (x – 3) (x – 1) – 0

⇒ x = 3, 1

At x = 1, f'(x) changes from positive to negative. Hence, x = 1 is point of local maxima

So, the maximum value is f(1) = (1)³ – 6(1)² + 9(1) + 15 = 19

At x = 3, f'(x) changes from negative to positive. Hence, x = 3 is point of local minima

So, the minimum value is f(x) = (3)³ – 6(3)² + 9(3) + 15 = 15

Question 7. f(x) = sin2x, 0 < x < π

Solution:

Given function

f(x) = sin2x, 0 < x, π

Now, differentiate the given function w.r.t. x

f'(x) = 2 cos 2x

Now, for local maxima and minima,

Put f'(x) = 0

⇒ 2x = 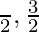$\frac{π}{2},\frac{3π}{2}$

⇒ x = 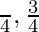$\frac{π}{4},\frac{3π}{4}$

At x = π/4, f'(x) changes from positive to negative. Hence, x = π/4, Is point of local maxima

So, the maximum value is f(π/4) = sin2(π/4) = 1

At x = 3π/4, f'(x) changes from negative to positive. Hence, x = 3π/4 is point of local minima,

So, the minimum value is f(3π/4) = sin2(3π/4) = -1

Question 8. f(x) = sin x – cos x, 0 < x < 2π

Solution:

Given function

f(x) = sin x – cos x, 0 < x < 2π

Now, differentiate the given function w.r.t. x

f'(x)= cos x + sin x

Now, for local maxima and minima,

Put f'(x) =0

cos x = -sin x

tan x = -1

x = $\frac{3π}{4},\frac{7π}{4}$ ∈ (0, 2π)

Now again differentiate the given function w.r.t. x

f”(x) = -sin x + cos x

$f"(\frac{3π}{4})=-sin\frac{3π}{4}+cos\frac{3π}{4}=-\frac{1}{√2}-\frac{1}{√2}=-√2$ <0

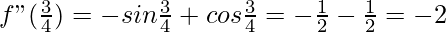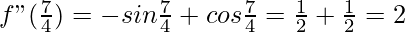$f"(\frac{7π}{4})=-sin\frac{7π}{4}+cos\frac{7π}{4}=\frac{1}{√2}+\frac{1}{√2}=√2$ >0

Therefore, by second derivative test, 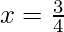$x=\frac{3π}{4}$ is a point of local maxima

Hence, the maximum value is 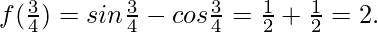$f(\frac{3π}{4})=sin\frac{3π}{4}-cos\frac{3π}{4}=\frac{1}{√2}+\frac{1}{√2}=√2.$

However, 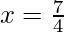$x=\frac{7π}{4}$ is a point of local minima

Hence, the minimum value is 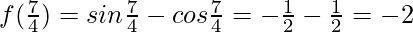$f(\frac{7π}{4})=sin\frac{7π}{4}-cos\frac{7π}{4}=-\frac{1}{√2}-\frac{1}{√2}=-√2$

Question 9. f(x) = cos x, 0< x < π

Solution:

Given function

f(x) = cos x, 0< x < π

Now, differentiate the given function w.r.t. x

f'(x) = – sin x

Now, for local maxima and minima,

Put f ‘(x) – 0

⇒ – sin x = 0

⇒ x = 0, and π

But, these two points lies outside the interval (0, π)

So, no local maxima and minima will exist in the interval (0, π).

Question 10. f(x) = sin 2x – x, -π/2 ≤ x ≤ π/2

Solution:

Given function

f(x) = sin2x – x

Now, differentiate the given function w.r.t. x

f ‘(x) = 2 cos 2x – 1

Now, for local maxima and minima,

Put f'(x) = 0

⇒ 2cos 2x – 1 = 0

⇒ cos 2x = 1/2 = cos π/3

⇒ 2x = π/3, -π/3

⇒ x = 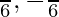$\frac{π}{6},-\frac{π}{6}$

At x = -π/6, f'(x) changes from negative to positive. Hence, x = π/6 is point of local minima.

So, the minimum value is 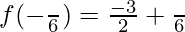$f(-\frac{π}{6})=\frac{-√3}{2}+\frac{π}{6}$

At x = π/6, f'(x) changes from positive to negative. Hence, x = π/6 is point of local maxima

The maximum value is 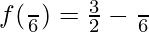$f(\frac{π}{6})=\frac{√3}{2}-\frac{π}{6}$

Question 11. f(x) = 2sin x – x, -π/2 ≤ x ≤ π/2

Solution:

Given function

f(x) = 2sin x – x, -π/2≤ x ≤ π/2

Now, differentiate the given function w.r.t. x

f ‘(x) = 2cos x – 1 = 0

Now, for local maxima and minima,

Put f'(x) = 0

⇒ cos x = 1/2 = cos π/3

⇒ x = -π/3, π/3

So, at x = -π/3, f'(x) changes from negative to positive. Hence, x = -π/3 is point of local minima

So, the minimum value is f(-π/3) = 2sin(-π/3) – (-π/3) = -√3 – π/3

At x = π/3, f'(x) changes from positive to negative. Hence, x = π/3 is point of local minima

The maximum value is f(π/3) = 2sin(π/3) – (π/3) = √3 – π/3

Question 12. f(x) = x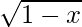 $\sqrt{1- x}$ , x > 0

Solution:

Given function

f(x) = x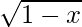 $\sqrt{1- x}$ , x > 0

Now, differentiate the given function w.r.t. x

f'(x) = 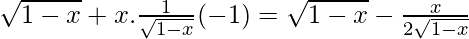$\sqrt{1- x}+ x.\frac{1}{\sqrt{1- x}}(-1)=\sqrt{1- x}-\frac{x}{2\sqrt{1- x}}$

= $\frac{2(1-x)-x}{2\sqrt{1- x}}=\frac{2-3x}{2\sqrt{1- x}}$

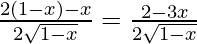
Now, for local maxima and minima,

Put f'(x) = 0

⇒ $\frac{2-3x}{2\sqrt{1-x}}=0$

⇒ 2 – 3x = 0

⇒ x = 2/3

f “(x) = $\frac{1}{2}[\frac{\sqrt{1-x}(-3)-(2-3x)(\frac{-1}{2\sqrt{1-x}})}{1-x}]$

= $\frac{\sqrt{1-x}(-3)+(2-3x)(\frac{1}{2\sqrt{1-x}})}{2(1-x)}$

= $\frac{-6(1-x)+(2-3x)}{4(1-x)^{3/2}}$

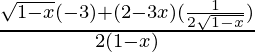
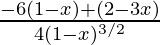
= (3x – 4)/4(1 – x)²

f “(2/3) = 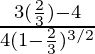$\frac{3(\frac{2}{3})-4}{4(1-\frac{2}{3})^{3/2}}$

= $\frac{2-4}{4(\frac{1}{3})^{3/2}}$

= $\frac{-1}{2(\frac{1}{3})^{3/2}}<0$

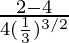
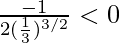
Therefore, x = 2/3 is a point of local maxima and the local maximum value of f at x = 2/3 is

f(2/3) = 2/3(√1/3) = (2√3)/9

Question 13. f(x) = x³(2x – 1)³

Solution:

Given function

f(x) = x³(2x – 1)³

Now, differentiate the given function w.r.t. x

f'(x) = 3x²(2x – 1)² + 6x³(2x – 1)²

= 3x²(2x – 1)²(2x – 1 + 2x)

= 3x²(4x – 1)

Now, for local maxima and minima,

Put f'(x) = 0

⇒ 3x²(4x – 1) = 0

⇒ x = 0, 1/4

At x = 1/4, f'(x) changes from negative to positive. Hence, x = 1/4 is the point of local minima,

So, the minimum value is f(1/4)= (1/4)³(2(1/4) – 1)³= -1/512

Question 14. f(x) = x/2 + 2/x, x > 0

Solution:

Given function

f(x) = x/2 + 2/x, x > 0

Now, differentiate the given function w.r.t. x

f'(x) = 1/2 – 2/x², x > 0

Now, for local maxima and minima,

Put f'(x) = 0

⇒ 1/2 – 2/x² = 0

⇒ x²– 4 = 0

⇒ x = 2, -2

At x = 2, f'(x) changes from negative to positive. Hence, x = 2 is point of local minima

So, the local minimum value is f(2) = 2/2 + 2/2 = 2

Question 15. f(x) = 1/(x²+ 2)

Solution:

Given function

f(x) = 1/(x²+ 2)

Now, differentiate the given function w.r.t. x

f'(x) = -(2x)/(x²+ 2)²

Now, for local maxima and minima,

Put f'(x) = 0 f'(x) = 0

f'(x) = -(2x)/(x²+ 2)² = 0

⇒ x = 0

At x = 0^–, f'(x) > 0

At x = 0⁺, f'(x) < 0

Therefore, local minimum and maximum value of f(0) = 1/2

Whether you're preparing for your first job interview or aiming to upskill in this ever-evolving tech landscape, GeeksforGeeks Courses are your key to success. We provide top-quality content at affordable prices, all geared towards accelerating your growth in a time-bound manner. Join the millions we've already empowered, and we're here to do the same for you. Don't miss out - check it out now!

Last Updated : 19 Apr, 2021

Class 12 RD Sharma Solutions - Chapter 18 Maxima and Minima - Exercise 18.1

Class 12 RD Sharma Solutions - Chapter 18 Maxima and Minima - Exercise 18.3

Chapter 1: Relations

Chapter 2: Functions

Chapter 3: Binary Operations

Chapter 4: Inverse Trigonometric Functions

Chapter 5: Algebra of Matrices

Chapter 6: Determinants

Chapter 7: Adjoint and Inverse of a Matrix

Chapter 8: Solutions of Simultaneous Linear Equations

Chapter 9: Continuity

Chapter 10: Differentiability

Chapter 11: Differentiation

Chapter 12: Higher Order Derivatives

Chapter 13: Derivative as a Rate Measurer

Chapter 14: Differentials, Errors, and Approximations

Chapter 15: Mean Value Theorems

Chapter 16: Tangents and Normals

Chapter 17: Increasing and Decreasing Functions

Chapter 18: Maxima and Minima

Chapter 19: Indefinite Integrals

Chapter 20: Definite Integrals

Chapter 21: Areas of Bounded Regions

Chapter 22: Differential Equations

Chapter 23: Algebra of Vectors

Chapter 24: Scalar Or Dot Product

Chapter 25: Vector or Cross Product

Chapter 26: Scalar Triple Product

Chapter 27: Direction Cosines and Direction Ratios

Chapter 28: Straight Line in Space

Chapter 29: The Plane

Chapter 30: Linear programming

Chapter 31: Probability

Chapter 32: Mean and Variance of a Random Variable

Chapter 33: Binomial Distribution

Chapter 1: Relations

Chapter 2: Functions

Chapter 3: Binary Operations

Chapter 4: Inverse Trigonometric Functions

Chapter 5: Algebra of Matrices

Chapter 6: Determinants

Chapter 7: Adjoint and Inverse of a Matrix

Chapter 8: Solutions of Simultaneous Linear Equations

Chapter 9: Continuity

Chapter 10: Differentiability

Chapter 11: Differentiation

Chapter 12: Higher Order Derivatives

Chapter 13: Derivative as a Rate Measurer

Chapter 14: Differentials, Errors, and Approximations

Chapter 15: Mean Value Theorems

Chapter 16: Tangents and Normals

Chapter 17: Increasing and Decreasing Functions

Chapter 18: Maxima and Minima

Chapter 19: Indefinite Integrals

Chapter 20: Definite Integrals

Chapter 21: Areas of Bounded Regions

Chapter 22: Differential Equations

Chapter 23: Algebra of Vectors

Chapter 24: Scalar Or Dot Product

Chapter 25: Vector or Cross Product

Chapter 26: Scalar Triple Product

Chapter 27: Direction Cosines and Direction Ratios

Chapter 28: Straight Line in Space

Chapter 29: The Plane

Chapter 30: Linear programming

Chapter 31: Probability

Chapter 32: Mean and Variance of a Random Variable

Chapter 33: Binomial Distribution

Class 12 RD Sharma Solutions – Chapter 18 Maxima and Minima – Exercise 18.2

Find the points of local maxima or local minima, if any, of the following functions, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be:

Question 1. f(x) = (x – 5)4

Question 2. f(x) = x3– 3x

Question 3. f(x) = x3 (x – 1)2

Question 4. f (x) = (x – 1) (x + 2)2

Question 5. f(x) = (x – 1)3 (x + 1)2

Question 6. f(x) = x3 – 6x2 + 9x +15

Question 7. f(x) = sin2x, 0 < x < π

Question 8. f(x) = sin x – cos x, 0 < x < 2π

Question 9. f(x) = cos x, 0< x < π

Question 10. f(x) = sin 2x – x, -π/2 ≤ x ≤ π/2

Question 11. f(x) = 2sin x – x, -π/2 ≤ x ≤ π/2

Question 12. f(x) = x, x > 0

Question 1. f(x) = (x – 5)⁴

Question 2. f(x) = x³– 3x

Question 3. f(x) = x³(x – 1)²

Question 4. f (x) = (x – 1) (x + 2)²

Question 5. f(x) = (x – 1)³(x + 1)²

Question 6. f(x) = x³ – 6x² + 9x +15

Question 12. f(x) = x $\sqrt{1- x}$ , x > 0

Question 13. f(x) = x³(2x – 1)³

Question 15. f(x) = 1/(x²+ 2)