Class 12 RD Sharma Solutions – Chapter 14 Differentials, Errors and Approximations – Exercise 14.1 | Set 2
Last Updated :
20 May, 2021
Question 9: Using differentials, find the approximate values of the following:
(xiv) 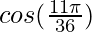
Solution:
Considering the function as
y = f(x) = cos x
Taking x = π/3, and
x+△x = 11π/36
△x = 11π/36-π/3 = -π/36
y = cos x
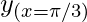 = cos (π/3) = 0.5
= cos (π/3) = 0.5
 = – sin x
= – sin x
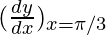 = – sin (π/3) = -0.86603
= – sin (π/3) = -0.86603
△y = dy = 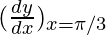 dx
dx
△y = (-0.86603) (-π/36)
△y = 0.0756
Hence, 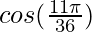 = 0.5+0.0756 = 0.5755
= 0.5+0.0756 = 0.5755
(xv) 
Solution:
Considering the function as
y = f(x) = 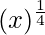
Taking x = 81, and
x+△x = 80
△x = 80-81 = -1
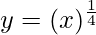

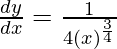

△y = dy = 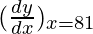 dx
dx
△y = 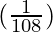 △x
△x
△y = 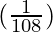 (-1) =
(-1) = 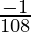 = -0.009259
= -0.009259
Hence,
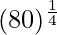 = y+△y = 3 + (-0.009259) = 2.99074
= y+△y = 3 + (-0.009259) = 2.99074
(xvi) 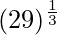
Solution:
Considering the function as
y = f(x) = 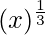
Taking x = 27, and
x+△x = 29
△x = 29-27 = 2
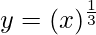



△y = dy = 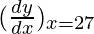 dx
dx
△y = 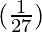 △x
△x
△y = 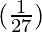 (2) = 0.074
(2) = 0.074
Hence,
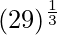 = y+△y = 3+0.074 = 3.074
= y+△y = 3+0.074 = 3.074
(xvii) 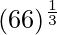
Solution:
Considering the function as
y = f(x) = 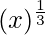
Taking x = 64, and
x+△x = 66
△x = 66-64 = 2
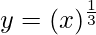
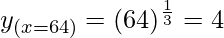


△y = dy = 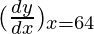 dx
dx
△y = 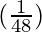 △x
△x
△y = 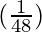 (2) = 0.042
(2) = 0.042
Hence,
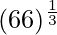 = y+△y = 4+0.042 = 4.042
= y+△y = 4+0.042 = 4.042
(xviii) 
Solution:
Considering the function as
y = f(x) = 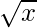
Taking x = 25, and
x+△x = 26
△x = 26-25 = 1
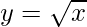

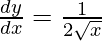
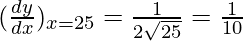
△y = dy = 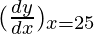 dx
dx
△y = 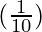 △x
△x
△y = 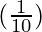 (1) = 0.1
(1) = 0.1
Hence,
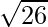 = y+△y = 5 + 0.1 = 5.1
= y+△y = 5 + 0.1 = 5.1
(xix) 
Solution:
Considering the function as
y = f(x) = 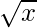
Taking x = 36, and
x+△x = 37
△x = 37-36 = 1
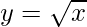
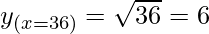
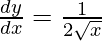
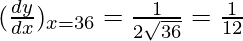
△y = dy = 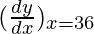 dx
dx
△y = 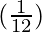 △x
△x
△y = 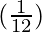 (1) = 0.0833
(1) = 0.0833
Hence,
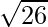 = y+△y = 6 + 0.0833 = 6.0833
= y+△y = 6 + 0.0833 = 6.0833
(xx) 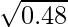
Solution:
Considering the function as
y = f(x) = 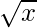
Taking x = 0.49, and
x+△x = 0.48
△x = 0.48-0.49 = -0.01
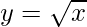
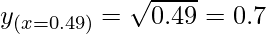
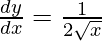
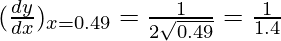
△y = dy = 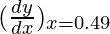 dx
dx
△y =  △x
△x
△y =  (-0.01) = -0.007143
(-0.01) = -0.007143
Hence,
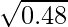 = y+△y = 0.7 + (-0.007143) = 0.693
= y+△y = 0.7 + (-0.007143) = 0.693
(xxi) 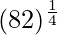
Solution:
Considering the function as
y = f(x) = 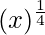
Taking x = 81, and
x+△x = 82
△x = 82-81 = 1
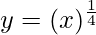

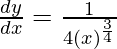

△y = dy = 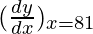 dx
dx
△y =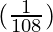 △x
△x
△y = 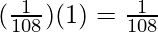 = 0.009259
= 0.009259
Hence,
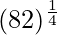 = y+△y = 3 + 0.009259 = 3.009259
= y+△y = 3 + 0.009259 = 3.009259
(xxii) 
Solution:
Considering the function as
y = f(x) = 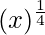
Taking x = 16/81, and
x+△x = 17/81
△x = 17/81-16/81 = 1/81
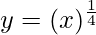
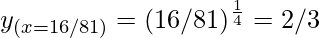
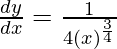
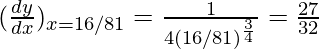
△y = dy =  dx
dx
△y =  △x
△x
△y =  = 0.01042
= 0.01042
Hence,
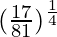 = y+△y = 2/3 + 0.01042 = 0.6771
= y+△y = 2/3 + 0.01042 = 0.6771
(xxiii) 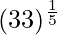
Solution:
Considering the function as
y = f(x) = 
Taking x = 32, and
x+△x = 33
△x = 33-32 = 1
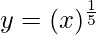
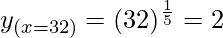
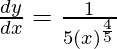
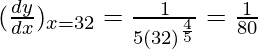
△y = dy = 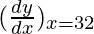 dx
dx
△y =  △x
△x
△y = 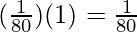 = 0.0125
= 0.0125
Hence,
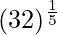 = y+△y = 2 + 0.0125 = 2.0125
= y+△y = 2 + 0.0125 = 2.0125
(xxiv) 
Solution:
Considering the function as
y = f(x) = 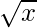
Taking x = 36, and
x+△x = 36.6
△x = 36.6-36 = 0.6
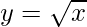
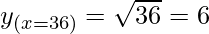
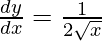
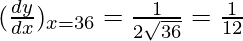
△y = dy = 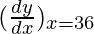 dx
dx
△y = 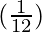 △x
△x
△y = 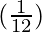 (0.6) = 0.05
(0.6) = 0.05
Hence,
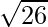 = y+△y = 6 + 0.05 = 6.05
= y+△y = 6 + 0.05 = 6.05
(xxv) 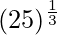
Solution:
Considering the function as
y = f(x) = 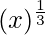
Taking x = 27, and
x+△x = 25
△x = 25-27 = -2
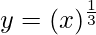



△y = dy = 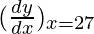 dx
dx
△y = 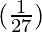 △x
△x
△y = 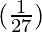 (-2) = -0.07407
(-2) = -0.07407
Hence,
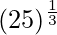 = y+△y = 3+(-0.07407) = 2.9259
= y+△y = 3+(-0.07407) = 2.9259
(xxvi) 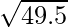
Solution:
Considering the function as
y = f(x) = 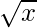
Taking x = 49, and
x+△x = 49.5
△x = 49.5-49 = 0.5
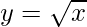

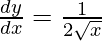
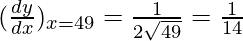
△y = dy =  dx
dx
△y = 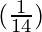 △x
△x
△y = 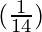 (0.5) = 0.0357
(0.5) = 0.0357
Hence,
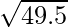 = y+△y = 7 + 0.0357 = 7.0357
= y+△y = 7 + 0.0357 = 7.0357
Question 10: Find the appropriate value of f(2.01), where f(x) = 4x2+5x+2
Solution:
Considering the function as
y = f(x) = 4x2+5x+2
Taking x = 2, and
x+△x = 2.01
△x = 2.01-2 = 0.01
y = 4x2+5x+2
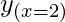 = 4(2)2+5(2)+2 = 28
= 4(2)2+5(2)+2 = 28
 = 8x+5
= 8x+5
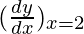 = 8(2)+5 = 21
= 8(2)+5 = 21
△y = dy = 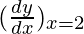 dx
dx
△y = (21) △x
△y = (21) (0.01) = 0.21
Hence,
f(2.01) = y+△y = 28 + 0.21 = 28.21
Question 11: Find the appropriate value of f(5.001), where f(x) = x3-7x2+15
Solution:
Considering the function as
y = f(x) = x3-7x2+15
Taking x = 5, and
x+△x = 5.001
△x =5.001-5 = 0.001
y = x3-7x2+15
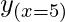 = (5)3-7(5)2+15 = -35
= (5)3-7(5)2+15 = -35
 = 3x2-14x
= 3x2-14x
 = 3(5)2-14(5) = 5
= 3(5)2-14(5) = 5
△y = dy =  dx
dx
△y = (5) △x
△y = (5) (0.001) = 0.005
Hence,
f(5.001) = y+△y = -35 + 0.005 = -34.995
Question 12: Find the appropriate value of log10 1005, given that log10 e=0.4343
Solution:
Considering the function as
y = f(x) = log10 x
Taking x = 1000, and
x+△x = 1005
△x =1005-1000 = 5
y = log10 x = 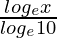
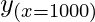 = log10 1000 = 3
= log10 1000 = 3
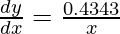
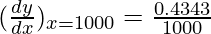 = 0.0004343
= 0.0004343
△y = dy = 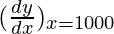 dx
dx
△y = (0.0004343) △x
△y = (0.0004343) (5) = 0.0021715
Hence, log10 1005 = y+△y = 3 + 0.0021715 = 3.0021715
Question 13: If the radius of a sphere is measured as 9cm with an error of 0.03m, find the approximate error in calculating its surface area.
Solution:
According to the given condition,
As, Surface area = 4πx2
Let △x be the change in the radius and △y be the change in the surface area
x = 9
△x = 0.03m = 3cm
x+△x = 9+3 = 12cm
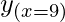 = 4πx2 = 4π(9)2 = 324 π
= 4πx2 = 4π(9)2 = 324 π
 = 8πx
= 8πx
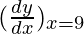 = 8π(9) = 72π
= 8π(9) = 72π
△y = dy = 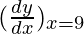 dx
dx
△y = (72π) △x
△y = (72π) (3) = 216 π
Hence, approximate error in surface area of the sphere is 216 π cm2
Question 14: Find the approximate change in the surface area of a cube as side x meters caused by decreasing the side by 1%.
Solution:
According to the given condition,
As, Surface area = 6x2
Let △x be the change in the length and △y be the change in the surface area
△x/x × 100 = 1
 = 6(2x) = 12x
= 6(2x) = 12x
△y = 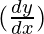 △x
△x
△y = (12x) (x/100)
△y = 0.12 x2
Hence, the approximate change in the surface area of a cubical box is 0.12 x2 m2
Question 15: If the radius of a sphere is measured as 7m with an error of 0.02m, find the approximate error in calculating its volume.
Solution:
According to the given condition,
As, Volume of sphere = 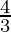 πx3
πx3
Let △x be the error in the radius and △y be the error in the volume
x = 7
△x = 0.02 cm
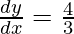 π(3x2) = 4πx2
π(3x2) = 4πx2
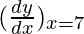 = 4π(7)2 = 196π
= 4π(7)2 = 196π
△y = dy = 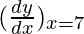 dx
dx
△y = (196π) △x
△y = (196π) (0.02) = 3.92 π
Hence, approximate error in volume of the sphere is 3.92 π cm2
Question 16: Find the approximate change in the volume of a cube as side x meters caused by increasing the side by 1%.
Solution:
According to the given condition,
As, Volume of cube = x3
Let △x be the change in the length and △y be the change in the volume
△x/x × 100 = 1
 = 3x2
= 3x2
△y = 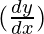 △x
△x
△y = (3x2) (x/100)
△y = 0.03 x3
Hence, the approximate change in the volume of a cubical box is 0.03 x3 m3
Share your thoughts in the comments
Please Login to comment...