Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.5 | Set 3
Last Updated :
26 May, 2021
Question 41. If (sin x)y = (cos y)x, prove that 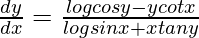 .
.
Solution:
We have,
=> (sin x)y = (cos y)x
On taking log of both the sides, we get,
=> log (sin x)y = log (cos y)x
=> y log (sin x) = x log (cos y)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com y[(\frac{1}{sinx})(cosx)]+log(sin x)(\frac{dy}{dx})=x[(\frac{1}{cosy})(-siny)(\frac{dy}{dx})]+log (cos y)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9495a761dfdac0495cbf8bb857a4db77_l3.png)
=> 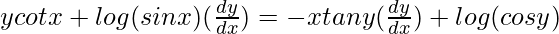
=> =log (cos y)-ycotx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-acd9499348c662a2d947ec4472d46270_l3.png)
=> 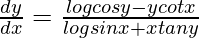
Hence proved.
Question 42. If (cos x)y = (tan y)x, prove that \frac{dy}{dx}=\frac{log tany+ytanx}{logcosx-xsecycosecy} .
Solution:
We have, (cos x)y = (tan y)x
On taking log of both the sides, we get,
=> log (cos x)y = log (tan y)x
=> y log (cos x) = x log (tan y)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com y[(\frac{1}{cosx})(-sinx)]+log (cos x)(\frac{dy}{dx})=x[(\frac{1}{tany})(sec^2y)(\frac{dy}{dx})]+log (tan y)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-319f16dfdd8dba7396576c3968383c86_l3.png)
=> 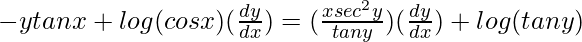
=> 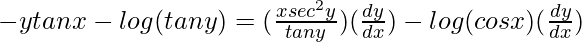
=> 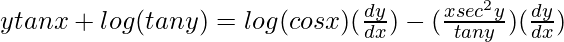
=> 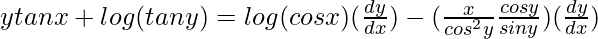
=> 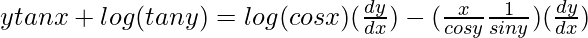
=> 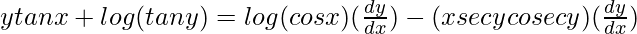
=> ![Rendered by QuickLaTeX.com ytanx+log (tan y)=[log(cos x)-(xsecycosecy)]\frac{dy}{dx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-41c3287ed89bb32809b9c90c60673d18_l3.png)
=> ![Rendered by QuickLaTeX.com [log(cos x)-(xsecycosecy)]\frac{dy}{dx}=ytanx+log (tan y)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a62e92ed4be44f89ac62d603fea03ee1_l3.png)
=> 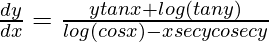
Hence proved.
Question 43. If ex + ey = ex+y, prove that 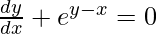 .
.
Solution:
We have,
=> ex + ey = ex+y
On differentiating both sides with respect to x, we get,
=> 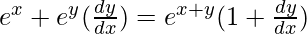
=> 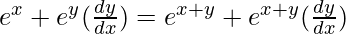
=> 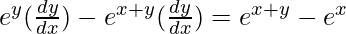
=> 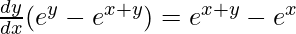
=> 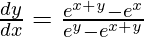
=> 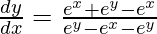
=> 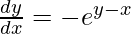
=> 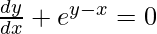
Hence proved.
Question 44. If ey = yx, prove that 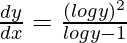 .
.
Solution:
We have,
=> ey = yx
On taking log of both the sides, we get,
=> log ey = log yx
=> y log e = x log y
=> y = x log y
On differentiating both sides with respect to x, we get,
=> 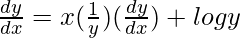
=> 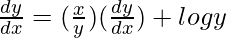
=> 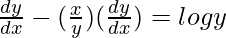
=> 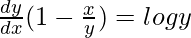
=> 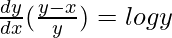
=> 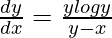
=> 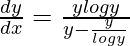
=> 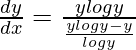
=> 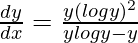
=> 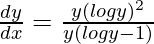
Hence proved.
Question 45. If ex+y − x = 0, prove that 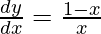 .
.
Solution:
We have,
=> ex+y − x = 0
On differentiating both sides with respect to x, we get,
=> 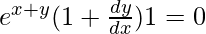
=> 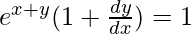
Now, we know ex+y − x = 0
=> ex+y = x
So, we get,
=> 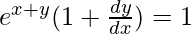
=> 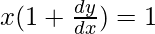
=> 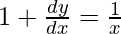
=> 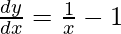
=> 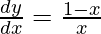
Hence proved.
Question 46. If y = x sin (a+y), prove that 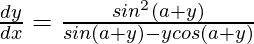 .
.
Solution:
We have,
=> y = x sin (a+y)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x[cos(a+y)(\frac{dy}{dx})]+sin(a+y))(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38846d15b2abc1f55965eaee168fa9c4_l3.png)
=> 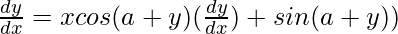
=> 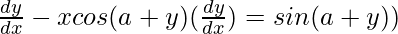
=> 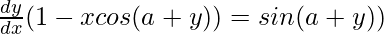
Now we know, y = x sin (a+y)
=> 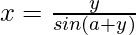
So, we get,
=> 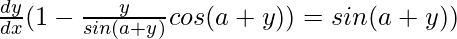
=> 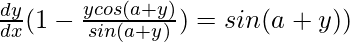
=> 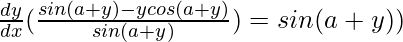
=> 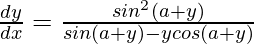
Hence proved.
Question 47. If x sin (a+y) + sin a cos (a+y) = 0, prove that 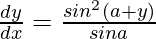 .
.
Solution:
We have,
=> x sin (a+y) + sin a cos (a+y) = 0
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com x(cos (a+y))(\frac{dy}{dx})+sin(a+y)(1)+sina [-sin(a+y)(\frac{dy}{dx})] = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10782ca6dadda0b33ffa316e8347ffe6_l3.png)
=> 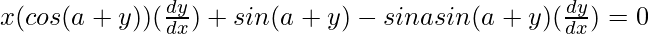
=> 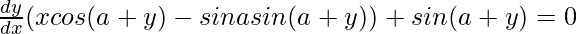
=> 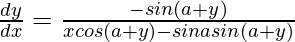
Now we know, x sin (a+y) + sin a cos (a+y) = 0
=> 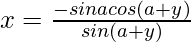
So, we get,
=> 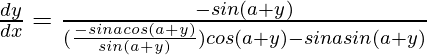
=> 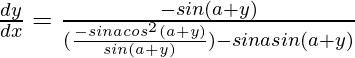
=> 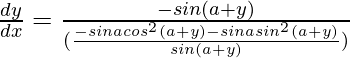
=> 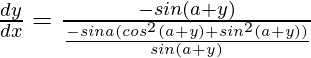
=> 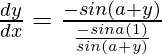
=> 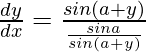
=> 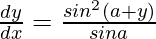
Hence proved.
Question 48. If (sin x)y = x + y, prove that 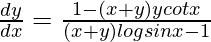 .
.
Solution:
We have,
=> (sin x)y = x + y
On taking log of both the sides, we get,
=> log (sin x)y = log (x + y)
=> y log sin x = log (x + y)
On differentiating both sides with respect to x, we get,
=> 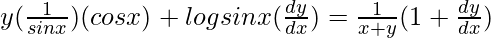
=> 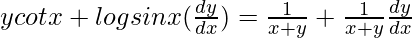
=> 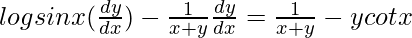
=> 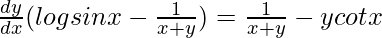
=> 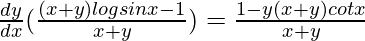
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}[(x+y)logsinx-1]=[1-y(x+y)cotx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4c274da3db2dc33b9657de004c2cee17_l3.png)
=> 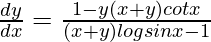
Hence proved.
Question 49. If xy log (x+y) = 1, prove that 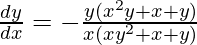 .
.
Solution:
We have,
=> xy log (x+y) = 1
On differentiating both sides with respect to x, we get,
=> 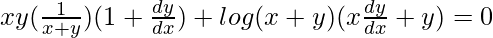
=> 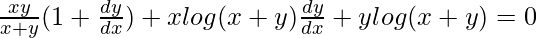
=> 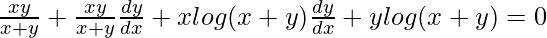
Now, we know, xy log (x+y) = 1.
=> 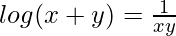
So, we get,
=> 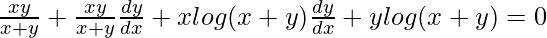
=> 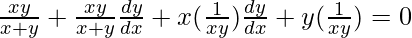
=> 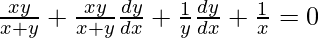
=> 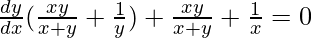
=> 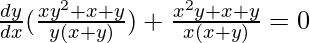
=> 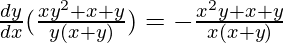
=> 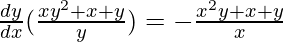
=> 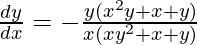
Hence proved.
Question 50. If y = x sin y, prove that 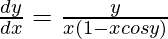 .
.
Solution:
We have,
=> y = x sin y
On differentiating both sides with respect to x, we get,
=> 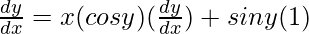
=> 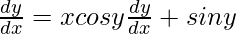
=> 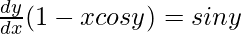
=> 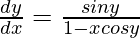
Now, we know y = x sin y
=> 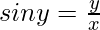
So, we get,
=> 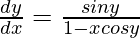
=> 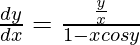
=> 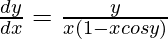
Hence proved.
Question 51. Find the derivative of the function f(x) given by,
f(x) = (1+x) (1+x2) (1+x4) (1+x8) and hence find f'(1).
Solution:
Here we are given,
=> f(x) = (1+x) (1+x2) (1+x4) (1+x8)
On differentiating both sides with respect to x, we get,
=> 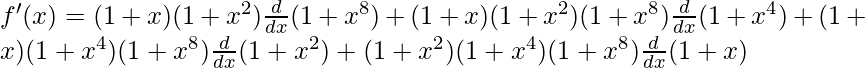
=> 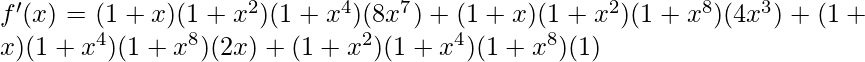
Now, the value of f'(x) at 1 is,
=> f'(1) = (1 + 1) (1 + 1) (1 + 1) (8) + (1 + 1) (1 + 1) (1 + 1) (4) + (1 + 1) (1 + 1) (1 + 1) (2) + (1 + 1) (1 + 1) (1 + 1) (1)
=> f'(1) = (2) (2) (2) (8) + (2) (2) (2) (4) + (2) (2) (2) (2) + (2) (2) (2) (1)
=> f'(1) = 64 + 32 + 16 + 8
=> f'(1) = 120
Therefore, the value of f'(1) is 120.
Question 52. If 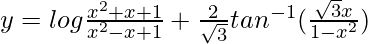 , find
, find 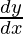 .
.
Solution:
We are given,
=> 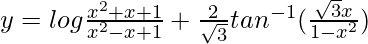
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{1}{\frac{x^2+x+1}{x^2-x+1}}\frac{d}{dx}(\frac{x^2+x+1}{x^2-x+1})+\frac{2}{\sqrt{3}}\left[\frac{1}{1+(\frac{\sqrt{3}x}{1-x^2})^2}\right]\frac{d}{dx}(\frac{\sqrt{3}x}{1-x^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46f01c999ec46901888fcc1bac445c0d_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{x^2-x+1}{x^2+x+1}\left[\frac{(x^2-x+1)(2x+1)-(x^2+x+1)(2x-1)}{(x^2-x+1)^2}\right]+\frac{2}{\sqrt{3}}\left[\frac{1}{1+\frac{3x^2}{(1-x^2)^2}}\right]\left[\frac{(1-x^2)(\sqrt{3})-\sqrt{3}x(-2x)}{(1-x^2)^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d41b09de98871a2ef0f4e80bb82362fd_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{1}{x^2+x+1}\left[\frac{2x^3+x^2-2x^2-x+2x+1-2x^3-2x^2-2x+x^2+x+1}{x^2-x+1}\right]+\frac{2}{\sqrt{3}}\left[\frac{1}{\frac{(1-x^2)^2+3x^2}{(1-x^2)^2}}\right]\left[\frac{\sqrt{3}-\sqrt{3}x^2+2\sqrt{3}x^2}{(1-x^2)^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d5f2ee27b32b20dbcf69357aec004a2_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{-2x^2+2}{x^4+2x^2+1-x^2}+\frac{2}{\sqrt{3}}\left[\frac{1}{\frac{1+x^4-2x^2+3x^2}{(1-x^2)^2}}\right]\left[\frac{\sqrt{3}+\sqrt{3}x^2}{(1-x^2)^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6426b89bf95e614846f3bf523c1e41ae_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{-2x^2+2}{x^4+x^2+1}+\frac{2}{\sqrt{3}}\left[\frac{(1-x^2)^2}{1+x^4-2x^2+3x^2}\right]\left[\frac{\sqrt{3}(1+x^2)}{(1-x^2)^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2680b9fc22ea05b8cf3aa39a6d8b9193_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{-2x^2+2}{x^4+x^2+1}+\frac{2}{\sqrt{3}}\left[\frac{\sqrt{3}(1+x^2)}{1+x^4+x^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-55e29c7fa8b6406edd95391ae34edea4_l3.png)
=> 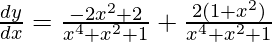
=> 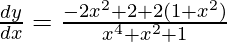
=> 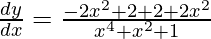
=> 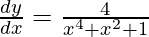
Question 53. If y = (sin x − cos x)sin x−cos x, π/4 < x < 3π/4, find 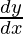 .
.
Solution:
We have,
=> y = (sin x − cos x)sin x−cos x
On taking log of both the sides, we get,
=> log y = log (sin x − cos x)sin x−cos x
=> log y = (sin x − cos x) log (sin x−cos x)
On differentiating both sides with respect to x, we get,
=> 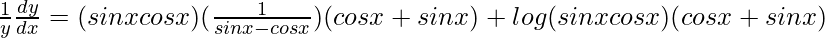
=> 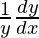 = (1)(cosx + sinx) + (cosx + sinx)log (sin x − cos x)
= (1)(cosx + sinx) + (cosx + sinx)log (sin x − cos x)
=> 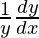 = cosx + sinx + (cosx + sinx)log (sin x − cos x)
= cosx + sinx + (cosx + sinx)log (sin x − cos x)
=> 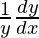 = (cosx + sinx)(1 + log (sin x − cos x))
= (cosx + sinx)(1 + log (sin x − cos x))
=>  = y(cosx + sinx)(1 + log (sin x − cos x))
= y(cosx + sinx)(1 + log (sin x − cos x))
=>  = (sinx – cosx)sinx-cosx(cosx + sinx)(1 + log (sin x − cos x))
= (sinx – cosx)sinx-cosx(cosx + sinx)(1 + log (sin x − cos x))
Question 54. Find dy/dx of function xy = ex-y.
Solution:
We have,
=> xy = ex-y
On taking log of both the sides, we get,
=> log xy = log ex-y
=> log x + log y = (x − y) log e
=> log x + log y = x − y
On differentiating both sides with respect to x, we get,
=> 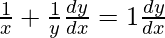
=> 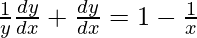
=> 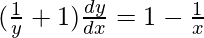
=> 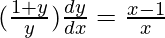
=> 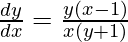
Question 55. Find dy/dx of function yx + xy + xx = ab.
Solution:
We have,
=> yx + xy + xx = ab
=> 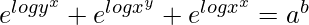
=> 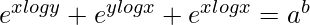
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com (e^{xlogy})[x(\frac{1}{y})(\frac{dy}{dx})+logy]+(e^{ylogx})[y(\frac{1}{x})+logx(\frac{dy}{dx})]+(e^{xlogx})[x(\frac{1}{x})+logx] = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9adf62163bd56bb066c24f14c3e519d6_l3.png)
=> ![Rendered by QuickLaTeX.com (e^{xlogy})[\frac{x}{y}\frac{dy}{dx}+logy]+(e^{ylogx})[\frac{y}{x}+logx(\frac{dy}{dx})]+(e^{xlogx})[1+logx] = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c02945dd8bcc3b6555956345de07faf3_l3.png)
=> ![Rendered by QuickLaTeX.com (y^x)[\frac{x}{y}\frac{dy}{dx}+logy]+(y^x)[\frac{y}{x}+logx(\frac{dy}{dx})]+(x^x)[1+logx] = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91323e045581b73e7ad362541ed3bb4c_l3.png)
=> 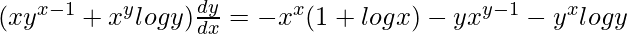
=> ![Rendered by QuickLaTeX.com (xy^{x-1}+x^ylogy)\frac{dy}{dx}=-[x^x(1+logx)+yx^{y-1}+y^xlogy]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-36092ca91841d3078f0d04f6fdb26f66_l3.png)
=> 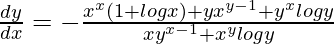
Question 56. If (cos x)y = (cos y)x, find dy/dx.
Solution:
We have,
=> (cos x)y = (cos y)x
On taking log of both the sides, we get,
=> log (cos x)y = log (cos y)x
=> y log (cos x) = x log (cos y)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com y[(\frac{1}{cosx})(-sinx)]+log (cos x)(\frac{dy}{dx})=x[(\frac{1}{cosy})(-siny)(\frac{dy}{dx})]+log(cos y)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8788158e8658cda1775f17bcb1e3172_l3.png)
=> 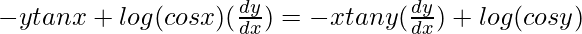
=> 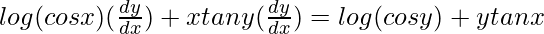
=> ![Rendered by QuickLaTeX.com [log (cos x)+xtany]\frac{dy}{dx}=log(cos y)+ytanx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3d4dd5d58e2c3022985c04e7841f083_l3.png)
=> 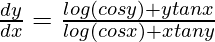
Question 57. If cos y = x cos (a+y), where cos a ≠ ±1, prove that 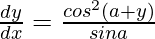 .
.
Solution:
We have,
=> cos y = x cos (a+y)
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com (-siny)(\frac{dy}{dx})=x[-sin (a+y)(\frac{dy}{dx})]+cos(a+y)(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-44e4970241c22b502c57857cd64e85f0_l3.png)
=> 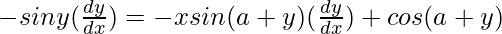
=> 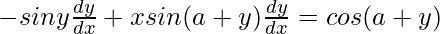
=> ![Rendered by QuickLaTeX.com [xsin(a+y)-siny]\frac{dy}{dx}=cos(a+y)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d9188aa60202023aa7c72688177874b8_l3.png)
=> 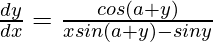
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{cos^2(a+y)}{cos(a+y)[xsin(a+y)-siny]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c389aa8f03aeda54fd1c650bf9424755_l3.png)
=> 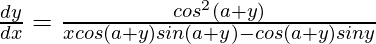
=> 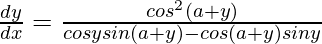
=> 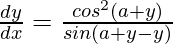
=> 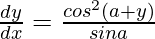
Hence proved.
Question 58. If 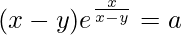 , prove that
, prove that 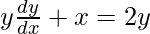 .
.
Solution:
We have,
=> 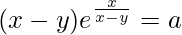
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com (x-y)\left[(e^{\frac{x}{x-y}})[\frac{(x-y)-x(1-\frac{dy}{dx})}{(x-y)^2}]\right]+e^{\frac{x}{x-y}}(1-\frac{dy}{dx})=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fafbadb72d57c59daaf76c2b69c135a5_l3.png)
=> 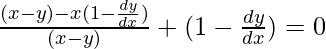
=> 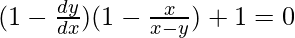
=> 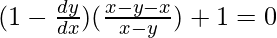
=> 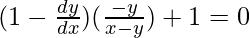
=> 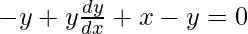
=> 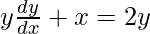
Hence proved.
Question 59. If 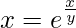 , prove that
, prove that 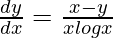 .
.
Solution:
We have,
=> 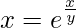
On taking log of both the sides, we get,
=> log x = log 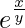
=> 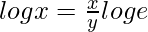
=> 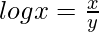
=> 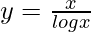
On differentiating both sides with respect to x, we get,
=> 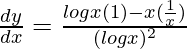
=> 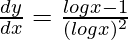
We know, 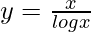
=> 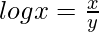
So, we get,
=> 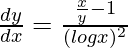
=> 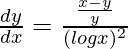
=> 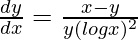
=> 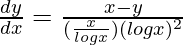
=> 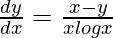
Hence proved.
Question 60. If 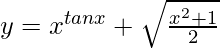 , find dy/dx.
, find dy/dx.
Solution:
We have,
=> 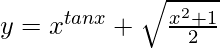
=> 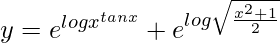
=> 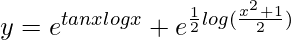
On differentiating both sides with respect to x, we get,
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{tanxlogx})[tanx(\frac{1}{x})+logx(sec^2x)]+(e^{\frac{1}{2}log(\frac{x^2+1}{2})})(\frac{1}{2})(\frac{2}{x^2+1})(\frac{1}{2})(2x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d3eb7c07593cbda6ebb9537983d28e4_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{tanxlogx})[\frac{tanx}{x}+sec^2xlogx]+(e^{\frac{1}{2}log(\frac{x^2+1}{2})})(\frac{x}{x^2+1})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-547397593fe8517e71f3843f1f5f2337_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x^{tanx}[\frac{tanx}{x}+sec^2xlogx]+\sqrt{\frac{x^2+1}{2}}(\frac{x}{x^2+1})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3884a4b0399c33d78d2d97ce734ec8ef_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{dy}{dx}=x^{tanx}[\frac{tanx}{x}+sec^2xlogx]+\frac{x}{\sqrt{2(x^2+1)}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-84ed21ac8dcac7b10c64611770c87d85_l3.png)
Question 61. If 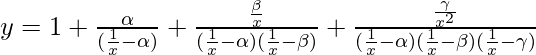 , find dy/dx.
, find dy/dx.
Solution:
We are given,
=> 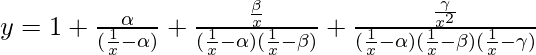
Now we know,
If 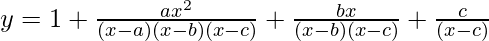 then,
then, ![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{y}{x}[\frac{a}{a-x}+\frac{b}{b-x}+\frac{c}{c-x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b108a4ca23d2ba8be59dadb7a4f23d90_l3.png)
In the given expression, we have 1/x instead of x.
So, using the above theorem, we get,
=> 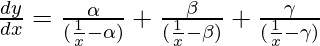
Share your thoughts in the comments
Please Login to comment...