Question 1.1 Find the sum of the following series to infinity : 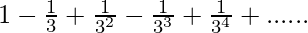
Solution:
Given series: 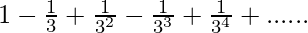
It is in the form of Geometric progression where first term=1 and common ratio=-1/3
We know that sum of G.P terms up to infinity is S=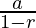 where a=first term and r=common ratio
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
S=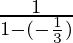
=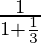
=3/4
Thus, 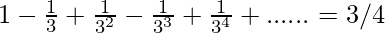
Question 1.2 Find the sum of the following series to infinity: 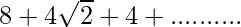
Solution:
Given series 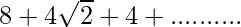
It is in the form of Geometric progression where first term=8 and common ratio=1/√2
We know that sum of G.P terms up to infinity is S=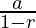
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
S=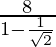
=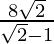
= 8√2(√2+1)
=16+8√2
Thus, 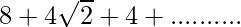 =16+8√2
=16+8√2
Question 1.3 Find the sum of the following series to infinity : 
Solution:
Given series 
⇒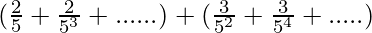
These two equations are in the form of Geometric progression
We know that sum of G.P terms up to infinity is S=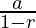
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
S=
=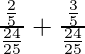
=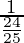
=25⁄24
Thus, 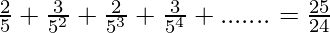
Question 1.4 Find the sum of the following series to infinity: 10-9+8.1-7.29+……….∞
Solution:
Given series: 10-9+8.1-7.29+……….∞
⇒ 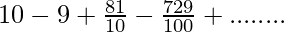
The above series are in Geometric Progression with first term=10 and common ratio=-9⁄10
We know that sum of G.P terms up to infinity is S=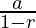
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
⇒ S=
⇒ S=100⁄19
Thus 
Question 1.5 Find the sum of the following series to infinity: 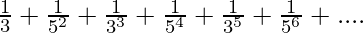
Solution:
Given series: 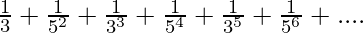
⇒ 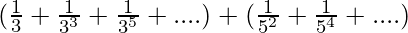
These two equations are in the form of Geometric progression
We know that sum of G.P terms up to infinity is S=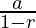
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
⇒ 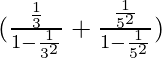
⇒ 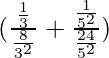
⇒ 3⁄8+1⁄24
⇒ 10⁄24
Thus, 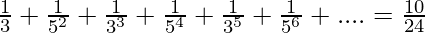
Question 2: Prove that 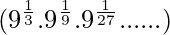
Solution:
Let us consider left hand side of the given equation
⇒ 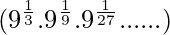
⇒ 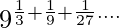
The equation 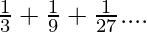 is in the form of Geometric progression where first term=1⁄3 and common ratio=1⁄3
is in the form of Geometric progression where first term=1⁄3 and common ratio=1⁄3
We know that sum of G.P terms up to infinity is S=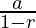
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
⇒ 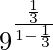
⇒ 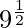
⇒ 3= Right hand side of the given equation
Thus we proved that 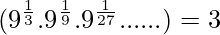
Question 3: Prove that 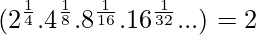
Solution:
Let us consider left hand side of the given equation
let S= 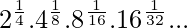
S=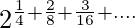
Denoting the terms in power with x
x=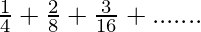 eq-(1)
eq-(1)
We can clearly see that this equation is neither in GP nor in AP. But the numerator of this equation is in AP and denominator in GP
let us multiply (1) with 1/2
![Rendered by QuickLaTeX.com \frac12x=\frac12[\frac14+\frac28+\frac3{16}+.....∞]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e38c05e412b11e7077f3d14df13b0184_l3.png) eq-(2)
eq-(2)
Let us subtract (2) from (1)
![Rendered by QuickLaTeX.com x-\frac{x}2=[\frac14+\frac28+\frac3{16}+....∞]-[\frac18+\frac2{16}+\frac3{32}+...∞]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab63fb8a1ca89b6e13709660bf109e65_l3.png)
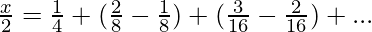
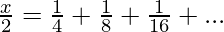
x=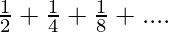
This equation is in the form of Geometric progression where first term=1/2 and common ratio=1/2
We know that sum of G.P terms up to infinity is S=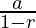
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
⇒ x=
⇒ x=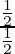
⇒ x=1
⇒S=2=Right hand side of the equation
Thus we proved that 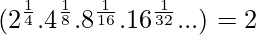
Question 4: If Sp denotes the sum of series 1+rp+r2p+…….∞ and sp the sum of the series 1 – rp+r2p+…….∞. Prove that Sp+sp=2S2p.
Solution:
Given Sp=1+rp+r2p+…….∞
The above equation is in Geometric progression where first term=1 and common ratio=rp
We know that sum of G.P terms up to infinity is S=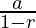
where a=first term and r=common ratio where r<1
Thus, on substituting the value of a and r in that formula
here |r|<1 ⇒|rp|<1
Sp=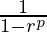 eq-(1)
eq-(1)
and sp=1 – rp+r2p+…….∞
The above equation is in Geometric progression where first term=1 and common ratio=-rp
We know that sum of G.P terms up to infinity is S=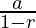
where a=first term and r=common ratio where r<1
Thus, on substituting the value of a and r in that formula
here |r|<1 ⇒|rp|<1
sp= eq-(2)
eq-(2)
on adding (1) and (2)
Sp+sp=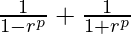
= 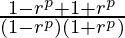
=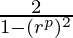
=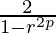 eq-(3)
eq-(3)
From (1) We can write 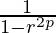 =S2p
=S2p
From (3), we can write that Sp+sp=2S2p
Hence proved.
Question 5: Find the sum of the terms of an infinite decreasing G.P in which all the terms are positive, the first term is 4 and the difference between the third and fifth term is equal to 32⁄81
Solution:
Let a denote the first term of G.P and r be the common ratio
we know that nth term of a G.P is given by an=arn-1
Given a=4 and a5-a3=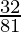
Here a5=4r4, a3=4r2
⇒ 4r4-4r2=32⁄81
⇒ 4r2(r2-1)=32⁄81
⇒ r2(r2-1)=8⁄81
let x=r2
⇒ x(x-1)=8⁄81
⇒ 81x2-81x-8=0
by using the formula of quadratic equation to solve the above equation, we get
x= 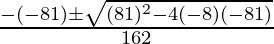
⇒ x=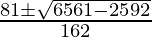
⇒ x=18⁄162 or x=144⁄162
⇒ x=1⁄9 or x=8⁄9
⇒ r2=1⁄9 or r2=8⁄9
⇒ r=1⁄3 or r=2√2/3
We know that sum of G.P terms up to infinity is S=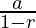
where a=first term and r=common ratio
Let us take 1st case a=4 and r=1⁄3
Then, S=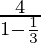
⇒ S=6
Now, in 2nd case a=4 and r=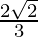
Then, S=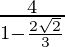
⇒ S=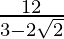
Thus the sum of the terms of an infinite decreasing G.P in which all the terms are positive are 6 and 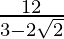
Question 6: Express the recurring decimal 0.125125125…. as a rational number.
Solution:
Let x=0.125125125…… eq-(1)
Here 125 is the repeating term
so,let us multiply both sides of the equation with a number such that complete repetitive part of number comes after decimal.
let us multiply (1) with 1000 in both sides ,we get
1000x=125.125125125…… eq-(2)
let us subtract (1) from (2)
1000x-x=125.0000
999x=125
x=125⁄999
Thus, 0.125125125…. can be expressed as 125/999
Question 7: Find the rational number whose decimal expansion is 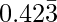
Solution:
Let x=0.423333333………… eq-(1)
here 3 is the repeating part .
So let us multiply both sides of equation (1) with a number such that complete repetitive part comes after decimal
Let us multiply (1) with 100
100x =42.33333………. eq-(2)
let us subtract (1) from (2)
100x-x=(42.3333333………..)-(0.4233333….)
99x =41.91
x=41.91/99
x=4191/9900
The rational number whose decimal expansion is 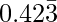 is 4191/9900
is 4191/9900
Question 8-1: Find the rational number having the following decimal expansion is 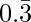
Solution:
let x=0.333333333333………..
x=0.3+0.03+0.003+………∞
x=3(0.1+0.01+0.001+……..∞)
x=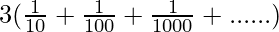
The above equation is in Geometric Progression with common ratio=1⁄10 and first term=1⁄10
We know that sum of G.P terms up to infinity is S=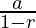
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
x=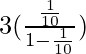
x=3×1⁄9
x=1⁄3
The rational number having decimal expansion is 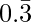 is 1⁄3
is 1⁄3
Question 8-2: Find the rational number having the following decimal expansion is 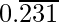
Solution:
let x=0.231231231………. eq-(1)
x=0.231+0.000231+0.000000231+……..∞
x=231(0.001+0.00001+0.0000001+……∞)
x=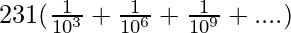
The above equation is in the form of Geometric Progression with first term=1⁄1000 common ratio=1⁄1000
We know that sum of G.P terms up to infinity is S=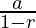
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
x=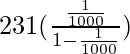
=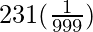
x=231/999
The rational number having decimal expansion is 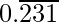 is 231/999
is 231/999
Question 8-3: Find the rational number having the following decimal expansion is 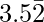
Solution:
let x=3.5222222……..
x=3.5+0.02+0.002+0.0002+…….∞
x=3.5+2(0.01+0.001+0.0001+…………∞)
let s= 0.01+0.001+0.0001+…………∞
s=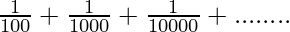
The above equation is in the form of Geometric Progression with first term=1⁄100 and common ratio=1⁄10
We know that sum of G.P terms up to infinity is S=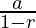
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
s=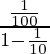
s =1⁄90
x=3.5+2s
=3.5+2×1⁄90
=35⁄10+1⁄45
=(315+2)/90
=317/90
The rational number having decimal expansion is 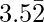 is 317/90.
is 317/90.
Question 8-4: Find the rational number having the following decimal expansion is 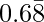
Solution:
let x=0.688888……….
x=0.6+0.08+0.008+0.0008+0.00008+…….∞
x=0.6+8(0.01+0.001+0.0001+……..∞)
let s=0.01+0.001+0.0001+………∞
s=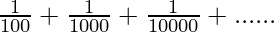
The above equation is in the form of Geometric Progression with first term= 1⁄100 and common ratio=1⁄10
We know that sum of G.P terms up to infinity is S=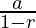
where a=first term and r=common ratio
Thus, on substituting the value of a and r in that formula
s=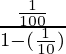
=1⁄90
x=0.6+8s
=0.6+8×1⁄90
=62⁄90
The rational number having decimal expansion is 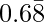 is 62/90
is 62/90
Question 9: One side of an equilateral triangle is 18cm. The midpoints of the sides are joined to form another triangle whose midpoints, in turn, are joined to form still another triangle. The process is continued indefinitely. Find the sum of the (i) perimeters of all the triangles (ii) Areas of all the triangles.
Solution:
According to Mid-Point Theorem, the sides of each triangle formed by joining the midpoints of an equilateral triangle are half of the sides of the equilateral triangle.
Thus, the sides of equilateral triangles formed are 18cm,9cm,4.5cm,2.25cm,…………….
i) Sum of perimeters of all the triangles
Let Sum of perimeters of all the triangles be P
P=3×18+3×9+3×4.5+3×2.25+………….∞
=3(18+9+9/2+9/4+……….∞)
It is in the form of G.P with first term=18 and common ratio=1⁄2
We know that sum of G.P terms up to infinity is S=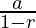
where a=first term and r=common ratio
P=3(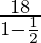 )
)
=3(18×2)
=3(36)=108
Thus, Sum of perimeters of all the triangles=108cms
ii) Sum of Areas of all the triangles
We know that the area of equilateral triangle =√3/4(a2)
where a is the length of the side of equilateral triangle.
Let Sum of Areas of all the triangles be A
A= √3/4(18)2+√3/4(9)2+√3/4(4.5)2+√3/4(2.25)2+…………….∞
=√3/4((18)2+(9)2+(4.5)2+(2.25)2+…………∞)
It is in the form of G.P with first term=(18)2 and common ratio=1⁄4
We know that sum of G.P terms up to infinity is S=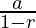
A= 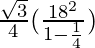
= (√3/3)×182
= 324/√3
= 108√3 cm2
Thus the Sum of Areas of all the triangles =108√3cm2
Question 10: Find an infinite G.P whose first term is 1 and each term is the sum of all the terms which follow it
Solution:
Given first term=1
let common ratio be r
Also given each term is the sum of all the terms which follow it
⇒ an=[an+1+an+2+an+3+……………∞] ∀ n∈ N
⇒ arn-1=arn+arn+1+arn+2+……………..∞ [since there are in G.P]
⇒ rn-1=rn+rn+1+rn+2+…………..∞
⇒ rn-1=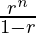
⇒ rn-1(1-r)=rn
⇒ rn-1-rn=rn
⇒ rn-1=2rn
⇒ 1=2r
⇒ r=1⁄2
Now, the infinite series will be a,ar,ar2,ar3………..∞
And thus the infinite G.P is 1,1⁄2,1⁄4,1⁄8,………………….∞
Question 11: The sum of the first two terms of infinite G.P is 5 and each term is three times the sum of the succeeding terms. Find the G.P.
Solution:
Let the first term be a and common difference be r in a given infinite G.P
Given a1+a2=5
⇒ a+ar=5 -(i)
Also, Given, an=3[an+1+an+2+an+3+………∞] ∀ n∈ N
⇒ arn-1=3[arn+1-1+arn+2-1+arn+3-1+………..∞]
=3[arn+arn+1+arn+2+………….∞]
=3arn[1+r+r2+………….∞]
=3arn\frac1{1-r}
arn-1=3arn\frac1{1-r}
⇒ r-1=3⁄1-r
⇒ 1-r=3r
⇒ 1=4r
⇒ r=1⁄4
On substituting the value of r in (i)
⇒ a+a(1⁄4)=5
⇒ a(1+1⁄4)=5
⇒ a(5⁄4)=5
⇒ a=4
Now, the G.P terms will be a,ar,ar2,ar3,……………∞
Thus, the G.P terms will be 4,1,1⁄4,1⁄16…………∞
Question 12: Show that in an infinite G.P with a common ratio r(|r|<1), each term bears a constant ratio to the sum of all terms that follow it.
Solution:
Let us Consider a infinite G.P series whose terms are a1,a2,a3,a4,a5…………∞ and common ratio r(|r|<1).
Also, let us assume the sum of all terms following each term will be S1,S2,S3,S4………….∞
we know that 1+r+r2+r3+r4+……………..∞=1⁄1-r
Now,S1=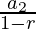 =
=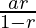
S2=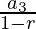 =
=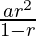
S3=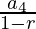 =
=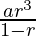
⇒ a1/S1=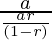 =(1-r)/r
=(1-r)/r
⇒a2/S2=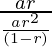 =(1-r)/r
=(1-r)/r
⇒ a3/S3=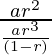 =(1-r)/r
=(1-r)/r
We can clearly observe that an/Sn=constant
Thus, we proved that ratio of each term to the sum of all the terms that follow it are constant.
Question 13: If S denotes the sum of infinite G.P. S1 denotes the sum of squares of its items, then prove that the first term and common ratio are respectively 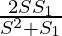 and
and 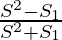
Solution:
Let us consider an infinite G.P series
let a be the first term and r be the common ratio in G.P series.
Given
a+ar+ar2+ar3+…………..∞=S
⇒ a(1+r+r2+r3+…………..∞)=S
⇒ a(1⁄1-r)=S eq-(1)
Also Given
S1=a2+a2r2+a2r4+…………..∞
=a2(1+r2+r4+………….∞)
=a2(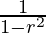 )
)
=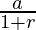 ×
×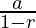
S1=S×(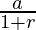 ) eq-(2)
) eq-(2)
Divide (2) by (1)
S1/S= 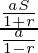
=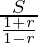
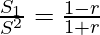
⇒ (1-r)S2=(1+r)S1
⇒ S2-S1=r(S2+S1)
⇒ r=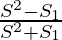
On substituting the value of r in (1)
S= 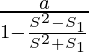
S = 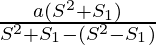
S= 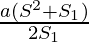
2SS1=a(S2+S1)
⇒ a=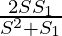
Thus, we proved that a=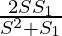 and r=
and r=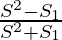
Share your thoughts in the comments
Please Login to comment...