Question 1. Find the sum of the following geometric progressions:
(i) 2, 6, 18, … to 7 terms
Solution:
Given G.P. has first term(a) = 2, common ratio(r) = 6/2 = 3 and number of terms(n) = 7
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
S7 = 2(37–1)/(3–1)
= 2(37–1)/2
= 2187–1
= 2186
Therefore, sum of 7 terms of the G.P. is 2186.
(ii) 1, 3, 9, 27, … to 8 terms
Solution:
Given G.P. has first term(a) = 1, common ratio(r) = 3 and number of terms(n) = 8
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
S8 = 1(38–1)/(3–1)
= 6560/2
= 3280
Therefore, sum of 8 terms of the G.P. is 3280.
(iii) 1, –1/2, 1/4, –1/8, ….
Solution:
Given G.P. has first term(a) = 1, common ratio(r) = –1/2 and number of terms(n) is infinite.
We know sum of n terms of an infinite GP is given by S = a/(1–r).
S = 1/[1 – (–1/2)]
= 1/(3/2)
= 2/3
Therefore, sum of infinite terms of the G.P. is 2/3.
(iv) (a2 – b2), (a – b), (a–b)/(a+b), … to n terms
Solution:
Given G.P. has first term(a) = (a2 – b2), common ratio(r) = (a – b)/(a2 – b2) = 1/(a+b) and number of terms is n.
We know sum of n terms of an infinite GP is given by Sn = a(rn–1)/(r–1).
Sn = ![Rendered by QuickLaTeX.com (a^2-b^2)\left[\frac{1-(\frac{1}{a+b})^n}{1-(\frac{1}{a+b})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1cb4ce8a57dbeae8883b023297b3dfe2_l3.png)
= 
= 
Therefore, sum of n terms of the G.P. is  .
.
(v) 4, 2, 1, 1/2 … to 10 terms
Solution:
Given G.P. has first term(a) = 4, common ratio(r) = 2/4 = 1/2 and number of terms(n) = 10.
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
S10 = ![Rendered by QuickLaTeX.com 4\left[\frac{(\frac{1}{2})^{10}-1}{(\frac{1}{2})-1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3331ec1f8cdd544042493b770bde7f53_l3.png)
= ![Rendered by QuickLaTeX.com 4\left[(\frac{1}{2})^{10}-1\right]×(-2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1c586afabd16a95f68f42bc51b109e9_l3.png)
= ![Rendered by QuickLaTeX.com (-8)\left[\frac{1 - 1024}{1024}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-434622b4372dfabae9553dc87f650c6b_l3.png)
= 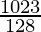
Therefore, sum of 10 terms of the G.P. is 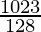 .
.
Question 2. Find the sum of the following geometric series:
(i) 0.15 + 0.015 + 0.0015 + … to 8 terms
Solution:
Given G.P. has first term(a) = 0.15, common ratio(r) = 0.015/0.15 = 1/10 and number of terms(n) = 8.
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
S8 = 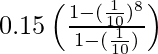
= 0.15 (10/9) (1 – 1/108)
= (1/6) (1 – 1/108)
Therefore, sum of 8 terms of the G.P. is (1/6) (1 – 1/108).
(ii) √2 + 1/√2 + 1/2√2 + …. to 8 terms
Solution:
Given G.P. has first term(a) = √2, common ratio(r) = (1/√2)/√2 = 1/2 and number of terms(n) = 8.
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
S8 = √2[(1/2)8–1]/[(1/2)–1]
= √2(1–1/256)/(1/2)
= √2 (255/256) (2)
= (255√2)/128
Therefore, sum of 8 terms of the G.P. is (255√2)/128.
(iii) 2/9 – 1/3 + 1/2 – 3/4 + … to 5 terms
Solution:
Given G.P. has first term(a) = 2/9, common ratio(r) = (–1/3)/(2/9) = –3/2 and number of terms(n) = 5.
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
S5 = ![Rendered by QuickLaTeX.com \frac{2}{9}\left[\frac{(\frac{3}{2})^5-1}{\frac{3}{2}-1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d24d9742dd4b4b99c6f1a7e229bddd98_l3.png)
= 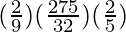
= 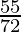
Therefore, sum of 5 terms of the G.P. is 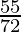 .
.
(iv) (x + y) + (x2 + xy + y2) + (x3 + x2y + xy2 + y3) + …. to n terms
Solution:
Given series can be written as,
Sn = (x + y) + (x2 + xy + y2) + (x3 + x2y + xy2 + y3) + . . . . to n terms
(x – y) Sn = (x + y) (x – y) + (x2 + xy + y2) (x – y) . . . to n terms
(x – y) Sn = x2 – y2 + x3 + x2y + xy2 – x2y – xy2 – y3 . . . to n terms
(x – y) Sn = (x2 + x3 + x4 + . . . n terms) + (y2 + y3 + y4 + . . . n terms)
(x – y) Sn = x2[(xn – 1)/(x – 1)] – y2[(yn – 1)/(y – 1)]
Sn = [x2[(xn – 1)/(x – 1)] – y2[(yn – 1)/(y – 1)]]/(x – y)
Therefore, sum of n terms of series is [x2[(xn – 1)/(x – 1)] – y2[(yn – 1)/(y – 1)]]/(x – y).
(v) 3/5 + 4/52 + 3/53 + 4/54 + … to n terms
Solution:
Given series can be written as,
Sn = (3/5 + 3/53 + . . . to n terms) + (4/52 + 4/54 + . . . to n terms)
= ![Rendered by QuickLaTeX.com \frac{3}{5}\left[\frac{(\frac{1}{25})^n-1}{(\frac{1}{25})-1}\right]+\frac{4}{25}\left[\frac{(\frac{1}{25})^n-1}{(\frac{1}{25})-1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-233461a2ff98c9439785c5b73dc938f8_l3.png)
= ![Rendered by QuickLaTeX.com \frac{5}{8}\left[1-\frac{1}{5^{2n}}\right]+\frac{1}{6}\left[1-\frac{1}{5^{2n}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7c3ce5783e64c52a53996c29ac92d208_l3.png)
= ![Rendered by QuickLaTeX.com \frac{19}{24}\left[1-\frac{1}{5^{2n}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b86ac97b70b24012caff9507b069724_l3.png)
Therefore, sum of n terms of series is ![Rendered by QuickLaTeX.com \frac{19}{24}\left[1-\frac{1}{5^{2n}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b86ac97b70b24012caff9507b069724_l3.png) .
.
(vi) 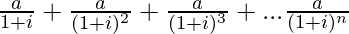
Solution:
Given G.P. has first term(a) = 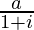 , common ratio(r) =
, common ratio(r) = 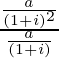 =
=  and number of terms is n.
and number of terms is n.
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
Sn = ![Rendered by QuickLaTeX.com \frac{a}{1+i}\left[\frac{1-(\frac{1}{1+i})^n}{1-\frac{1}{1+i}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06e1f606f4cd3c9f353cd7a12ddadd65_l3.png)
= ![Rendered by QuickLaTeX.com (\frac{a}{1+i})(\frac{1+i}{-i})[1-(1+i)^n]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a82f200ffc02d72e1e4faa8b14163a41_l3.png)
= –a i[1–(1+i)-n]
Therefore, sum of n terms of G.P. is –a i[1–(1+i)-n].
(vii) 1, –a, a2, –a3, . . . . to n terms (a ≠ 1)
Solution:
Given G.P. has first term(a) = 1, common ratio(r) = –a and number of terms is n.
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
Sn = [(–a)n–1]/(–a–1)
= [1–(–a)n]/(a+1)
Therefore, sum of n terms of G.P. is [1–(–a)n]/(a+1).
(viii) x3 + x5 + x7 + . . . . n terms
Solution:
Given G.P. has first term(a) = x, common ratio(r) = x5/x3 = x2 and number of terms is n.
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
= x3[x2n–1]/[x2–1]
Therefore, sum of n terms of G.P. is x3[x2n–1]/[x2–1].
(ix) √7 + √21 + 3√7 + . . . . n terms
Solution:
Given G.P. has first term(a) = √7, common ratio(r) = √21/√7 = √3 and number of terms = n.
We know sum of n terms of a GP is given by Sn = a(rn–1)/(r–1).
Sn = √7[(√3)n–1]/(√3–1)
Therefore, sum of n terms of G.P. is √7[(√3)n–1]/(√3–1).
Question 3. Evaluate the following:
(i) 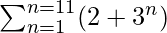
Solution:
Given summation can be written as,
S11 = (2+31) + (2+32) + (2+33) + . . . . + (2+311)
= 2(11) + (31 + 32 + 33 + . . . . 311)
= 2(11) + 3(311–1)/(3–1)
= 22 + 265719
= 265741
Therefore, value of the summation is 265741.
(ii) 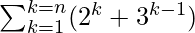
Solution:
Given summation can be written as,
Sn = (2+30) + (22+31) + (23+32) + . . . . + (2n+3n-1)
= (21 + 22 + 23 + . . . . + 2n) + (30 + 31 + 32 + . . . . + 3n-1)
= 2(2n–1)/(2–1) + 30(3n–1)/(3–1)
= 2(2n–1) + (3n–1)/2
Therefore, value of the summation is 2(2n–1) + (3n–1)/2.
(iii) 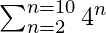
Solution:
Given summation can be written as,
S10-2+1 = S9 = 42 + 43 + 44 + . . . . 410
= 42(49–1)/(4–1)
= 16[49–1]/3
Therefore, value of the summation is 16[49–1]/3.
Question 4. Find the sum of the series:
(i) 5 + 55 + 555 + … to n terms
Solution:
We have Sn = 5 + 55 + 555 + ….. up to n terms.
Multiplying and dividing by 9, we get
= 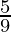 [9+99+999+…to n terms]
[9+99+999+…to n terms]
= 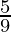 [(10–1)+(102–1)+(103–1)…to n terms]
[(10–1)+(102–1)+(103–1)…to n terms]
= 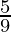 [(10+102+103+….n terms) – (1+1+1+…..n terms)]
[(10+102+103+….n terms) – (1+1+1+…..n terms)]
= ![Rendered by QuickLaTeX.com \frac{5}{9}\left[\frac{10(10^n-1)}{10-1}-n\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-83de2911ecd8d139355d05f3c3c436ba_l3.png)
= 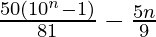
Therefore, the sum of the series up to n terms is 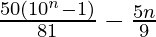 .
.
(ii) 7 + 77 + 777 + … to n terms
Solution:
We have Sn = 7 + 77 + 777 + … to n terms.
Multiplying and dividing by 9, we get,
= 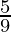 [9+99+999+…to n terms]
[9+99+999+…to n terms]
= 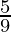 [(10–1)+(102–1)+(103–1)…to n terms]
[(10–1)+(102–1)+(103–1)…to n terms]
= 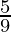 [(10+102+103+….n terms) – (1+1+1+…..n terms)]
[(10+102+103+….n terms) – (1+1+1+…..n terms)]
= ![Rendered by QuickLaTeX.com \frac{7}{9}\left[\frac{10(10^n-1)}{10-1}-n\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12588562bdd20da0924be4bbc7d94184_l3.png)
= 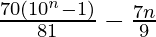
Therefore, the sum of the series up to n terms is 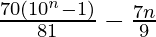 .
.
(iii) 9 + 99 + 999 + … to n terms
Solution:
We have Sn = 9 + 99 + 999 + … to n terms. It can be written as,
= (10–1)+(102–1)+(103–1)…to n terms
= (10+102+103+….n terms) – (1+1+1+…..n terms)
= ![Rendered by QuickLaTeX.com \left[\frac{10(10^n-1)}{10-1}-n\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab43cb0af27b4ba343ab462054d642d9_l3.png)
Therefore, the sum of the series up to n terms is ![Rendered by QuickLaTeX.com \left[\frac{10(10^n-1)}{10-1}-n\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab43cb0af27b4ba343ab462054d642d9_l3.png) .
.
(iv) 0.5 + 0.55 + 0.555 + … to n terms
Solution:
We have Sn = 0.5 + 0.55 + 0.555 + … to n terms. It can be written as,
= ![Rendered by QuickLaTeX.com \frac{5}{9}\left[\frac{9}{10}+\frac{99}{100}+\frac{999}{1000}+...n \hspace{0.1cm}terms\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f898cd5f2a5776fe343513220171ee84_l3.png)
= ![Rendered by QuickLaTeX.com \frac{5}{9}\left[(1-\frac{1}{10})+(1-\frac{1}{100})+(1-\frac{1}{1000})+...n\hspace{0.1cm}terms\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef91ad36c8400bfd31cd05631eafabcb_l3.png)
= ![Rendered by QuickLaTeX.com \frac{5}{9}\left[(1+1+1...n\hspace{0.1cm}terms)-(\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}+...n\hspace{0.1cm}terms)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5765df48925af41940076c86620acb97_l3.png)
= ![Rendered by QuickLaTeX.com \frac{5}{9}\left[n-\frac{(\frac{1}{10})(1-(\frac{1}{10})^n}{1-\frac{1}{10}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7fb61eced455a53801979f113f541eeb_l3.png)
= 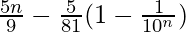
Therefore, the sum of the series up to n terms is 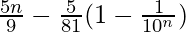 .
.
(v) 0.6 + 0.66 + 0.666 + … to n terms
Solution:
We have Sn = 0.6 + 0.66 + 0.666 + … to n terms. It can be written as,
= ![Rendered by QuickLaTeX.com \frac{6}{9}\left[\frac{9}{10}+\frac{99}{100}+\frac{999}{1000}+...n \hspace{0.1cm}terms\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a1374f445b937135c9bdfc24818a295_l3.png)
= ![Rendered by QuickLaTeX.com \frac{6}{9}\left[(1-\frac{1}{10})+(1-\frac{1}{100})+(1-\frac{1}{1000})+...n\hspace{0.1cm}terms\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d95d9355dc2c366338ca4fd73a526ae1_l3.png)
= ![Rendered by QuickLaTeX.com \frac{6}{9}\left[(1+1+1...n\hspace{0.1cm}terms)-(\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}+...n\hspace{0.1cm}terms)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-691747dcbcc3556c77898b52174d2925_l3.png)
= ![Rendered by QuickLaTeX.com \frac{6}{9}\left[n-\frac{(\frac{1}{10})(1-(\frac{1}{10})^n}{1-\frac{1}{10}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3b8b6859ebd50d5e71cf1a3819afe7c_l3.png)
= 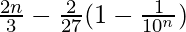
Therefore, the sum of the series up to n terms is 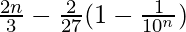 .
.
Question 5. How many terms of the G.P. 3, 3/2, 3/4, … be taken together to make 3069/512?
Solution:
Given G.P. has first term(a) = 3, common ratio(r) = (3/2)/3 = 1/2 and sum of terms(Sn) = 3069/512.
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
=> 3069/512 = 3[1–(1/2)n] / [1–(1/2)]
=> 2(2n–1)/(2n) = 1023/512
=> 1023(2)n = 1024(2)n – 1024
=> 2n = 1024
=> n = 10
Therefore, 10 terms of the G.P. should be taken together to make 3069/512.
Question 6. How many terms of the series 2 + 6 + 18 + …. must be taken to make the sum equal to 728?
Solution:
Given G.P. has first term(a) = 2, common ratio(r) = 6/2 = 3 and sum of terms(Sn) = 728.
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
=> 728 = 2[3n–1]/[3–1]
=> 3n–1 = 728
=> 3n = 729
=> n = 6
Therefore, 6 terms of the G.P. must be taken together to make the sum equal to 728.
Question 7. How many terms of the sequence √3, 3, 3√3,… must be taken to make the sum 39+ 13√3 ?
Solution:
Given G.P. has first term(a) = 2, common ratio(r) = 3/√3 = 1/√3 and sum of terms(Sn) = 39+ 13√3.
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
=> 39+13√3 = √3[3n/2–1]/(√3–1)
=> (39+13√3)(√3–1) = √3(3n/2–1)
=> 39√3–39+39–13√3 = 3(n+1)/2–√3
=> 3(n+1)/2 = 27√3
=> 3n/2 √3 = 27√3
=> 3n/2 = 27
=> n/2 = 3
=> n = 6
Therefore, 6 terms of the G.P. must be taken to make the sum 39+ 13√3.
Question 8. The sum of n terms of the G.P. 3, 6, 12, … is 381. Find the value of n.
Solution:
Given G.P. has first term(a) = 3, common ratio(r) = 6/3 = 2 and sum of terms(Sn) = 381.
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
=> 381 = 3(2n–1)/(2–1)
=> 2n – 1 = 127
=> 2n = 128
=> n = 7
Therefore, value of n is 7.
Question 9. The common ratio of a G.P. is 3, and the last term is 486. If the sum of these terms be 728, find the first term.
Solution:
Given G.P. has common ratio(r) = 3, last term(an) = 486 and sum of terms(Sn) = 728.
We know nth term of a G.P. is given by an = arn-1.
=> 486 = a(3)n-1
=> 486 = a(3)n/3
=> a(3)n = 1458 . . . . (1)
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
=> 728 = a(3n–1)/(3–1)
=> 1456 = a(3)n–a
Using (1) in the equation, we get,
=> a = 1458 – 1456 = 2
Therefore, first term of the G.P. is 2.
Question 10. The ratio of the sum of the first three terms is to that of the first 6 terms of a G.P. is 125 : 152. Find the common ratio.
Solution:
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
According to the question, we have,
=> 
=> (r3–1)/(r6–1) = 125/152
=> 1/(r3+1) = 125/152
=> 125r3 + 125 = 152
=> r3 = 27/125
=> r = 3/5
Therefore, the common ratio is 3/5.
Question 11. The 4th and 7th term of a G.P. are 1/27 and 1/729 respectively. Find the sum of n terms of the G.P.
Solution:
We know nth term of a G.P. is given by an = arn-1.
According to the question, we have,
=> ar3 = 1/27 . . . . (1)
=> ar6 = 1/729 . . . . (2)
Dividing (2) by (1), we get,
=> r3 = 27/729 = 1/27
=> r = 1/3
Putting r = 1/3 in (1), we get,
=> a(1/3)3 = 1/27
=> a(1/27) = 1/27
=> a = 1
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
=> Sn = 1[(1/3)n–1]/[(1/3)–1]
= 3[1–(1/3)n]/2
Therefore, sum of n terms of the G.P. is 3[1–(1/3)n]/2.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...