Class 11 RD Sharma Solutions – Chapter 20 Geometric Progressions- Exercise 20.3 | Set 2
Last Updated :
19 Apr, 2021
Question 12. Find the sum: 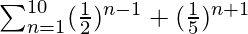
Solution:
Given summation can be written as,
S = 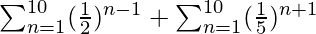
= (1 + 1/2 + 1/22 + . . . . 10 terms) + (1/52 + 1/53 + 1/54 + . . . . 10 terms)
= ![Rendered by QuickLaTeX.com \left[\frac{1-\frac{1}{2^{10}}}{1-\frac{1}{2}}\right]+\left[\frac{1-\frac{1}{5^{10}}}{1-\frac{1}{5}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-efa34464096a51822104e6d8bf5aeee1_l3.png)
= 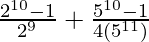
Therefore, sum of the series is 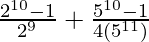 .
.
Question 13. The fifth term of a G.P. is 81 whereas its second term is 24. Find the series and sum of its first eight terms.
Solution:
We know nth term of G.P. is given by, an = arn-1.
According to the question, we have,
=> ar4 = 81 . . . . (1)
=> ar = 24 . . . . (2)
Dividing (2) by (1),
=> r3 = 81/24
=> r3 = 27/8
=> r = 3/2
Putting r = 3/2 in (2), we get,
=> a = (24)(2)/3
=> a = 16
We know sum of n terms of G.P. is given by, Sn = a(rn−1)/(r−1).
So, S8 = 16[(3/2)8−1]/[(3/2)−1]
= 16[38 − 28]/27
= 6305/8
As a = 16 and r = 3/2, series would be 16, 24, 36, 54, . . . .
Also, the sum of first 8 terms of G.P. is 6305/8.
Question 14. If S1, S2, S3 be respectively the sum of n, 2n, 3n terms of a G.P., then prove that S21+S22 = S1(S2+S3).
Solution:
We are given,
S1 = Sum of n terms = a[1−rn]/(1−r)
S2 = Sum of 2n terms = a[1−r2n]/(1−r)
S3 = Sum of 3n terms = a[1−r3n]/(1−r)
We have,
L.H.S. = S21+S22
= ![Rendered by QuickLaTeX.com \left[\frac{a(1-r^n)}{1-r}\right]^2+\left[\frac{a(1-r^{2n})}{1-r}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06650088fa3c1358c5f7f4c3c000d3be_l3.png)
= ![Rendered by QuickLaTeX.com \frac{a^2}{(1-r)^2}[(1-r^n)^2+(1-r^{2n})^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e9e5ffb22dab8bcec1265a7e01f0d79c_l3.png)
= ![Rendered by QuickLaTeX.com \frac{a^2}{(1-r)^2}[1+r^{2n}-2r^n+1+r^{4n}-2r^{2n}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4f21da62aeeeb714222ba3200b70de0b_l3.png)
= ![Rendered by QuickLaTeX.com \frac{a^2}{(1-r)^2}[2-r^{2n}-2r^n+r^{4n}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f2c7118b375670964bcad81df51a875_l3.png)
And R.H.S. = S1(S2+S3)
= ![Rendered by QuickLaTeX.com \frac{a(1-r^n)}{1-r}\left[\frac{a(1-r^{2n})}{1-r}+\frac{a(1-r^{3n})}{1-r}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a9c8361651533f7b5f58b4af63d47dc_l3.png)
= ![Rendered by QuickLaTeX.com \frac{a^2}{(1-r)^2}[(1-r^n)(1-r^{2n})+(1-r^n)(1-r^{3n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c58cad9fd53a468e49c54731d6c7f6b1_l3.png)
= ![Rendered by QuickLaTeX.com \frac{a^2}{(1-r)^2}[1-r^{2n}-r^n+r^{3n}+1-r^{3n}-r^n+r^{4n}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd25077b32ce776221078617b47f56eb_l3.png)
= ![Rendered by QuickLaTeX.com \frac{a^2}{(1-r)^2}[2-r^{2n}-2r^n+r^{4n}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f2c7118b375670964bcad81df51a875_l3.png)
= L.H.S.
Hence, proved.
Question 15. Show that the ratio of the sum of n terms of a G.P. to the sum of terms from (n+1)th to (2n)th term is 1/rn.
Solution:
We know sum of n terms of a G.P. is given by, S1 = a[1−rn]/(1−r).
And sum of terms from (n+1)th to (2n)th term will be,
S2 = arn + arn+1 + arn+2 + . . . . ar2n-1
= arn[1−rn]/(1−r)
L.H.S. = 
= 1/rn
= R.H.S.
Hence, proved.
Question 16. If a and b are the roots of x2 – 3x + p = 0 and c, d are roots of x2 – 12x + q = 0, where a, b, c, d, form a G.P. Prove that (q + p):(q – p) = 17:15.
Solution:
We are given that a, b, c, d are in G.P. Let’s suppose the common ratio is r.
So, b=ar, c=ar2 and d=ar3
Now a and b are the roots of x2 – 3x + p = 0.
Sum of roots = a + b = 3
=> a + ar = 3
=> a(1+r) = 3 ….. (1)
Product of roots = ab = p
=> a(ar) = p
=> a2r = p ….. (2)
And c, d are the roots of x2 − 12x + q = 0
Sum of roots = c + d = 12
=> ar2 + ar3 = 12
=> ar2(1+r) = 12 ….. (3)
Product of roots = cd = q
=> ar2(ar3) = q
=> a2r5 = q ….. (4)
Dividing equation (3) by (1), we get,
=> 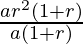 =
= 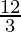
=> r2 = 4
=> r = ±2
When r=2, from (1), we get,
=> a(1+2) = 3
=> a = 1
Putting a=1 and r=2 in (2),
=> p = (1)2(2) = 2
From (4) we get,
q = (1)2(2)5 = 32
Now L.H.S. = 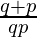 =
=  =
= 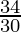 =
= 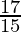
= R.H.S.
When r=−2, from (1), we get,
=> a(1−2) = 3
=> a = −3
Putting a=−3 and r=−2 in (2),
p = (−3)2(−2) = −18
From (4) we get,
q = (−3)2(−2)5 = −288
Now L.H.S. = 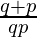 =
= 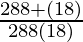 =
= 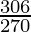 =
= 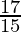
= R.H.S.
Hence, proved.
Question 17. How many terms of the G.P. 3, 3/2, 3/4, … are needed to give the sum 3069/512?
Solution:
Given G.P. has first term(a) = 3, common ratio(r) = (3/2)/3 = 1/2 and sum of terms(Sn) = 3069/512.
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
=> 3069/512 = 3[1–(1/2)n] / [1–(1/2)]
=> 2(2n–1)/(2n) = 1023/512
=> 1023(2)n = 1024(2)n – 1024
=> 2n = 1024
=> n = 10
Therefore, 10 terms of the G.P. should be taken together to make 3069/512.
Question 18. A person has 2 parents, 4 grandparents, 8 great grandparents, and so on. Find the number of his ancestors during the ten generations preceding his own.
Solution:
We have the sequence, 2,4,8, . . . . which forms a G.P. with first term(a) = 2 and common ratio(r) = 4/2 = 2.
We know sum of n terms of a G.P. is given by Sn = a(rn–1)/(r–1).
Number of ancestors during the ten generations = Sum of first 10 terms of the G.P.
S10 = 2(210–1)/(2–1)
= 2(1023)
= 2046
Therefore, the number his ancestors during the ten generations preceding his own is 2046.
Question 19. S1, S2, S3, . . . ., Sn are the sums of n terms of G.P.’s whose first term is 1 in each and common ratios are 1,2,3, . . . ., n respectively, then prove that S1 + S2 + 2S3 + 3S4 + . . . . + (n–1)Sn = 1n + 2n + 3n + . . . . + nn.
Solution:
S1, S2, S3, . . . ., Sn are the sums of n terms of G.P.’s whose first term is 1 in each and common ratios are 1,2,3, . . . ., n respectively.
Here for S1, series will be 1,1,1,1, . . . up to n terms as first term(a) and common ratio(r) both are equal to 1.
So, S1 = 1+1+1+1+ . . . . up to n terms = n
So, L.H.S. = S1 + S2 + 2S3 + 3S4 + . . . . + (n–1)Sn
= 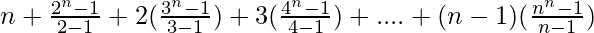
= n + (2n – 1) + (3n – 1) + (4n – 1) + . . . . (nn – 1)
= n + (2n + 3n + 4n +. . . . + nn) – (1 + 1 +1 + 1 + . . . . (n–1) terms)
= n + (2n + 3n + 4n +. . . . + nn) – n + 1
= 1 + 2n + 3n + 4n +. . . . + nn
= 1n + 2n + 3n + 4n +. . . . + nn
= R.H.S.
Hence, proved.
Question 20. A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of the terms occupying the odd places. Find the common ratio of the G.P.
Solution:
As number of terms is even, let the number of terms of the G.P. be 2n.
According to the question,
Sum of all terms = 5 (Sum of the terms occupying the odd places)
=> a1 + a2 + a3 + . . . . + an = 5 (a1 + a3 + a5 + . . . . a2n–1)
=> a + ar + ar2 + . . . . + arn–1 = 5 (a + ar2 + ar4 + . . . . + ar2n–2)
=> a(1–r2n)/(1–r) = 5a(1–r2n)/(1–r2)
=> a/(1–r) = 5a/(1–r2)
=> a/(1–r) = 5a/[(1–r)(1+r)]
=> 5/(1+r) = 1
=> 1+r = 5
=> r = 4
Therefore, the common ratio of the G.P. is 4.
Question 21. Let an be the nth term of the G.P. of positive numbers. Let  and
and  , such that α ≠ β. Prove that the common ratio of the G.P. is α/β.
, such that α ≠ β. Prove that the common ratio of the G.P. is α/β.
Solution:
We have, 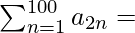
=> a2 + a4 + a6 + . . . . + a200 = α
=> ar + ar3 + ar5 + . . . . + ar199 = α
=> ar(r2(100)–1)/(r–1) = α
=> ar(r200–1)/(r–1) = α . . . . (1)
Also we have, 
=> a1 + a3 + a5 + . . . . + a199 = β
=> a + ar2 + ar4 + . . . . + ar198 = β
=> a(r2(100)–1)/(r–1) = β
=> a(r200–1)/(r–1) = β . . . . (2)
Dividing (2) by (1), we get,
=>  =
= 
=> r = 
Hence, proved.
Question 22. Find the sum of 2n terms of the series whose every even term is ‘a’ times the term before it and every odd term is ‘c’ times the term before it, the first term being unity.
Solution:
Suppose we have the series, a1,a2,a3, . . . . an.
According to the question, we have, a1 = 1, a2 = a, a3 = ca, a4 = a2c, a5 = a2c2 and so on.
Now, sum of 2n terms of the series = a1 + a2 + a3 + . . . . + a2n
S2n = 1 + a + ca + a2c + a2c2 + . . . . 2n terms
= (1+a) + ca(1+a) + a2c2(1+a) + . . . . n terms
Now this is a G.P. with first term(a) = (1+a) and common ratio(r) = ca. So, we get
S2n = ![Rendered by QuickLaTeX.com \frac{(1+a)[(ac)^n-1]}{ac-1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1dbdf1a6ddfe1890b486877710d1ce77_l3.png)
Therefore, sum of 2n terms of the series is ![Rendered by QuickLaTeX.com \frac{(1+a)[(ac)^n-1]}{ac-1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1dbdf1a6ddfe1890b486877710d1ce77_l3.png) .
.
Share your thoughts in the comments
Please Login to comment...