Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.6
Last Updated :
11 Feb, 2021
Question 1. If 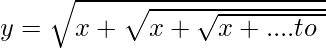 , prove that
, prove that 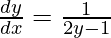
Solution:
We have, 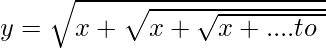
⇒ 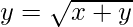
Squaring both sides, we get,
y2 = x + y
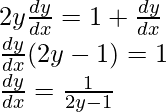
Question 2. If 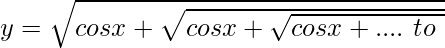 , prove that
, prove that 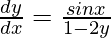
Solution:
We have, 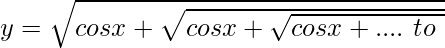
⇒ 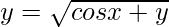
Squaring both sides, we get,
y2 = cos x + y
⇒ 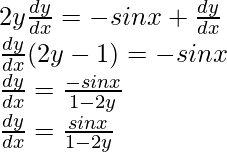
Question 3. If 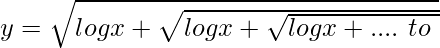 , prove that
, prove that 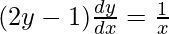
Solution:
We have, 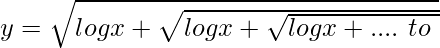
⇒ 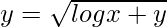
Squaring both sides, we get,
y2 = log x + y
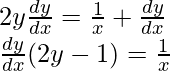
Question 4. If 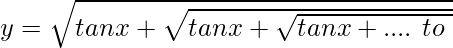 , prove that
, prove that 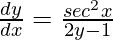
Solution:
We have, 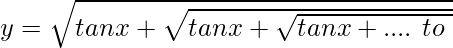
⇒ 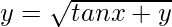
Squaring both sides, we get,
y2 = tan x + y
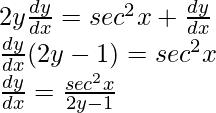
Question 5. If 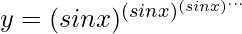 , prove that
, prove that 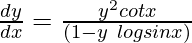
Solution:
We have, 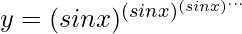
⇒ y = (sin x)y
Taking log on both sides,
log y = log(sin x)y
⇒ log y = y log(sin x)
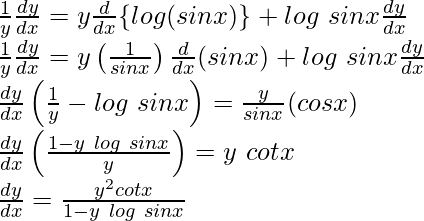
Question 6. If 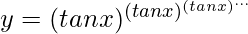 , prove that
, prove that 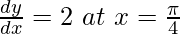
Solution:
We have, 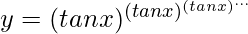
⇒ y = (tan x)y
Taking log on both sides,
log y = log(tan x)y
⇒ log y = y log tan x
Differentiating with respect to x using chain rule,
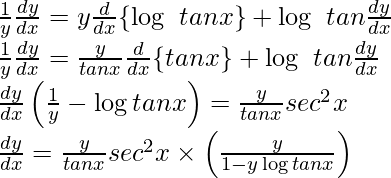
Now,
![Rendered by QuickLaTeX.com \left(\frac{dy}{dx}\right)_{x=\frac{\pi}{4}}=\frac{y\ sec^2\left(\frac{\pi}{4}\right)}{tan\left(\frac{\pi}{4}\right)}\times\frac{y}{1-y\ \log tan\left(\frac{\pi}{4}\right)}\\ ⇒\left(\frac{dy}{dx}\right)_{x=\frac{\pi}{4}}=\frac{y^2(\sqrt{2})^2}{1(1-y\log\ tan1)}\\ ⇒\left(\frac{dy}{dx}\right)_{x=\frac{\pi}{4}}=\frac{2(1)^2}{(1-0)}\ \ \ \ \ \left[\because\ (y)_{\frac{\pi}{4}}=\left(tan\frac{\pi}{4}\right)^{\left(tan\frac{\pi}{4}\right)^{\left(tan\frac{\pi}{4}\right)^{...\infin}}}=1\right]\\ ⇒\left(\frac{dy}{dx}\right)_{x=\frac{\pi}{4}}=2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb824bed13d29c199f6f62705bcba9c2_l3.png)
Question 7. If 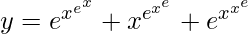 , prove that
, prove that 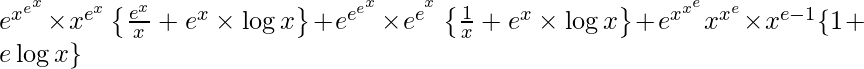
Solution:
We have, 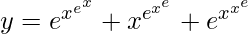
⇒ y = u + v + w
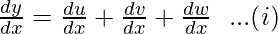
where 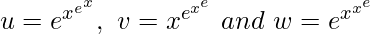
Now, 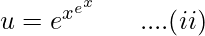
Taking log on both sides,
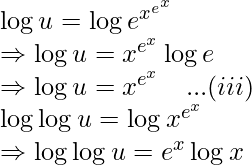
Differentiating with respect to x,
![Rendered by QuickLaTeX.com \Rightarrow\frac{1}{\log u}\frac{d}{dx}(\log u)=e^x\frac{d}{dx}(\log x)+\log x\frac{d}{dx}(e^x)\\ \Rightarrow\frac{1}{\log u}\frac{1}{u}\frac{du}{dx}=\frac{e^x}{x}+e^x\log x\\ \Rightarrow\frac{du}{dx}=u\log u\left[\frac{e^x}{x}+e^x\log x\right]\\ \Rightarrow\frac{du}{dx}=e^{x^{e^x}}\times x^{e^{x}}\left[\frac{e^x}{x}+e^x\log x\right]\\ Now,\ v=x^{e^{x^e}}\ \ \ \ \ ...(iv)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8196b4a5adcf9be76655977505118101_l3.png)
Taking log on both sides,
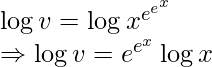
Taking log on both sides
![Rendered by QuickLaTeX.com \Rightarrow\frac{1}{\log w}\frac{d}{dx}(\log w)=x^e\frac{d}{dx}(\log x)+\log x\frac{d}{dx}(x^e)\\ \Rightarrow\frac{1}{\log w}\left(\frac{1}{w}\right)\frac{dw}{dx}=x^e\left(\frac{1}{x}\right)+\log xex^{e-1}\\ \Rightarrow\frac{dw}{dx}=w\log w[x^{e-1}+e\log xx^{e-1}]\\ \Rightarrow\frac{dw}{dx}=e^{x^{x^e}}x^{x^{e}}x^{e-1}(1+e\log x)\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-766c16d20bbaa007d59d9722e36a1588_l3.png)
Using equation in equation (i), we get
![Rendered by QuickLaTeX.com \frac{dy}{dx}=e^{x^{e^x}}{x^{e^x}}\left[\frac{e^x}{x}+e^x\log x\right]+x^{e^{e^x}}\times e^{e^x}\left[\frac{1}{x}+e^x\log x\right]+e^{x^{x^e}}{x^{x^e}}x^{e-1}(1+e\log x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab370608e18275a99a5fc96cfd1d1952_l3.png)
Question 8. If 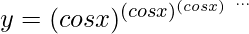 , Prove that
, Prove that 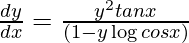
Solution:
We have, 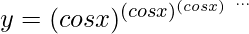
⇒ y = (cos x)y
Taking log on both sides,
log y = log(cos x)y
⇒ log y = y log (cos x)
Differentiating with respect to x using chain rule,
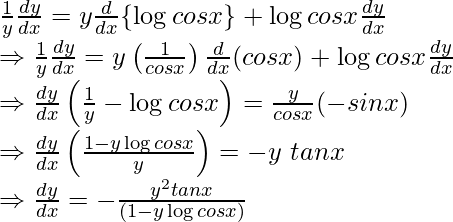
Share your thoughts in the comments
Please Login to comment...