Class 10 RD Sharma Solutions – Chapter 5 Trigonometric Ratios – Exercise 5.1 | Set 2
Last Updated :
21 Feb, 2021
Question 7. If cotθ = 7/8, evaluate:
(i) 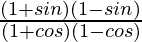
(ii) cot2θ
Solution:
cotθ = 7/8 = Base/Perpendicular
In right-angled ΔPQR,
∠Q = 90°, PQ = 8, RQ = 7

Using Pythagoras Theorem
PR2 = PQ2 + QR2
PR2 = 82 + 72 = 64 + 49
PR2 = 113
PR = √113
Now
sinθ = Perpendicular/Hypotenuse = PQ/PR = 8/√113
cosθ = Base/Hypotenuse = QR/PR = 7/√113
(i) 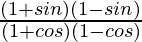
Putting the values of sinθ and cosθ in the equation
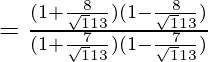
=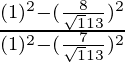
=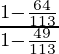

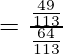
= 49/64
(ii) cot2θ
= (cosθ/sinθ)2
Putting the values of sinθ and cosθ in the following equation
=![Rendered by QuickLaTeX.com [\frac{(\frac{7}{\sqrt113})}{(\frac{8}{\sqrt113})}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a3bb177c0f2fc83eb32cfe16c331859_l3.png)
=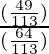
= 49/64
or
cot2θ = (cotθ)2 = (7/8)2 = 49/64
Question 8. If 3 cot A = 4, check whether 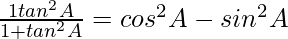 or not.
or not.
Solution:
Given, 3cot A = 4 or cot A = 4/3
Draw a △ ABC where ∠B = 90°, AB = 4, BC = 3

Using Pythagoras Theorem
AC2 = AB2 + BC2
AC2 = 42 + 32 = 16 + 9
AC2 = 25
AC = 5
Now,
Taking LHS
=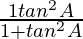
=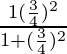
=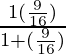
=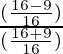
= 7/25
Taking RHS
= cos2A – sin2A
=(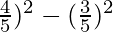
=(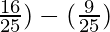
=(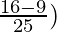
= 7/25
RHS = LHS (Hence Proved)
Question 9. If tanθ = a/b, find the value of 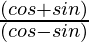
Solution:
Given, tanθ = a/b
Draw a △ABC where ∠B = 90°, AB = b, BC = a

Using Pythagoras Theorem
AC2 = BC2 + AB2
AC2 = a2 + b2
AC2 = 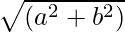
Now,
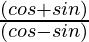
=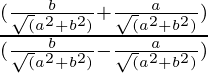
=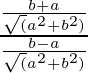
= (b + a)/(b – a)
Question 10. If 3tanθ = 4, find the value of 
Solution:
Given tanθ = 4/3

Now, Dividing the numerator and denominator by cosθ
=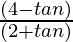
Putting the values of tanθ in the above equation
=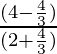
=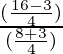
= 8/10
= 4/5
Question 11. If 3cotθ = 2, find the value of 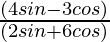
Solution:
Given: 3cotθ = 2

Using Pythagoras Theorem
AC2 = BC2 + AB2
AC2 = 32 + 42
AC2 = 9 + 16 = 25
AC = 5
Now,
=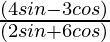
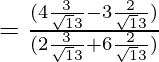

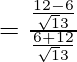
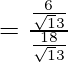
= 6/18 = 1/3
Question 12. If tanθ = a/b, prove that 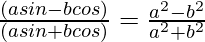
Solution:
Given, tanθ = a/b

Using Pythagoras Theorem
AC2 = BC2 + AB2
AC2 = a2 + b2
AC2 = 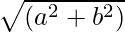
Now,
=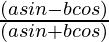
Putting the values of sinθ and cosθ in the above equation
=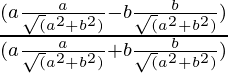
=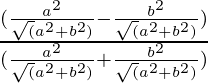
=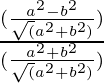
=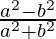
Hence Proved
Question 13. If secθ = 13/5, prove that 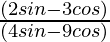 =3
=3
Solution:
Given, secθ = 13/5

Using Pythagoras Theorem
AC2 = BC2 + AB2
132 = BC2 + 52
BC2 = 169 – 25 = 144
BC = 12
Now,
Taking LHS
=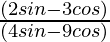
Putting the values of sinθ and cosθ in the above equation
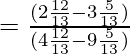
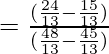
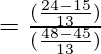
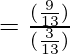
= 3 = RHS
Hence Proved
Question 14. If cosθ = 12/13, show that sinθ(1 – tanθ) = 35/156
Solution:
We have cosθ = 12/13

Using Pythagoras Theorem
AC2 = BC2 + AB2
132 = BC2 + 122
BC2 = 169 – 144 = 25
BC = 5
Now,
Taking LHS
= sinθ(1 – tanθ)
=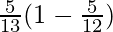
=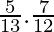
= 35/156
= RHS
Hence Proved
Question 15. If cotθ = 1/√3, show that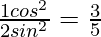
Solution:
Given, cotθ = 1/√3
tanθ = 1/cotθ =√3

From Pythagoras theorem,
AC2 = AB2 + BC2
AC2 = 12 + (√3)2
AC2 = 3 + 1 = 4
AC = 2
Now,
Taking LHS
=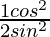
=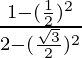
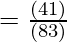
= 3/5
Hence Proved
Question 16. If tanθ = 1/√7, then 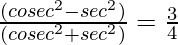
Solution:
We have
tanθ = 1/√7
cotθ = √7
We know sec2θ = (1 + tan2θ) = 1 + 1/7 = 8/7
and cosec2θ = (1 + cot2θ) = 1 + 7 = 8
Now,
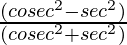
=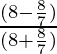
= 48/64 = 3/4
Question 17. If secθ = 5/4, find the value of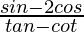
Solution:
Given:
secθ = 5/4
cosθ = 1/secθ = 4/5

From Pythagoras theorem,
AC2 = BC2 + AB2
52 = BC2 + 42
BC2 = 25 − 16 = 9
BC = 3
Now,
=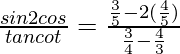
=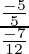
= 12/7
Question 18. If tanθ = 12/13, find the value of 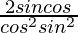
Solution:
Given: tanθ = 12/13
From Pythagoras theorem,
AC2 = BC2 + AB2
AC2 = (13)2 + (12)2
AC2 = 313
AC = √313
sinθ = 12/√313
cosθ = 13/√313
We have
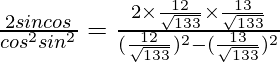
= \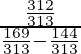
= 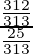
= 312/25
Question 19. If cosθ = 3/5, then evaluate 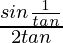
Solution:
Given:
cosθ = 3/5

From Pythagoras theorem,
AC2 = BC2 + AB2
52 = 32 + AB2
AB2 = 25 − 9 = 16
AB = 4
Now
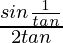
=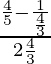
=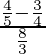
=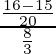
= (1/20) × (3/8)
= 3/160
Question 20. If sinθ = 3/5, then evaluate 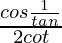
Solution:
Given,
sinθ = 3/5
Now
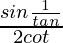
=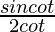
=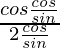
=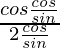
=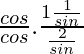
=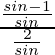
= (sinθ – 1)/(2)
Putting the value of sinθ, we get
=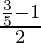
=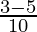
= -1/5
Question 21. If tanθ = 24/7, find that sinθ + cosθ.
Solution:
Given:
tanθ = 24/7

From Pythagoras theorem,
AC2 = BC2 + AB2
AC2 = 242 + 72
AC2 = 576 + 49 = 625
AC = 25
Now,
= sinθ + cosθ
= 24/25 + 7/25
= (24 + 7)/25
= 31/25
Share your thoughts in the comments
Please Login to comment...