Question 1. Express each of the following as the sum or difference of sines and cosines:
(i) 2 sin 3θ cos θ
Solution:
By using the trigonometric identity,
2 sin A cos B = sin (A+B) + sin (A-B)
Taking A = 3θ and B = θ
2 sin 3θ cos θ = sin (3θ+θ) + sin (3θ-θ)
= sin 4θ + sin 2θ
(ii) 2 cos 3θ sin 2θ
Solution:
By using the trigonometric identity,
2 sin A cos B = sin (A+B) + sin (A-B)
Taking A = 2θ and B = 3θ
2 cos 3θ sin 2θ = sin (3θ+2θ) + sin (2θ-3θ)
= sin 5θ + sin (-θ)
= sin 5θ – sin θ
(iii) 2 sin 4θ sin 3θ
Solution:
By using the trigonometric identity,
2 sin A sin B = cos (A-B) – cos (A+B)
Taking A = 4θ and B = 3θ
2 sin 4θ sin 3θ = cos (4θ-3θ) – cos (4θ+3θ)
= cos θ – cos 7θ
(iv) 2 cos 7θ cos 3θ
Solution:
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
Taking A = 7θ and B = 3θ
2 cos 7θ cos 3θ = cos (7θ+3θ) + cos (7θ-3θ)
= cos 10θ – cos 4θ
Question 2. Prove that:
(i) 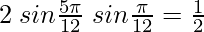
Solution:
By using the trigonometric identity,
2 sin A sin B = cos (A-B) – cos (A+B)
Taking A =  and B =
and B = 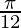
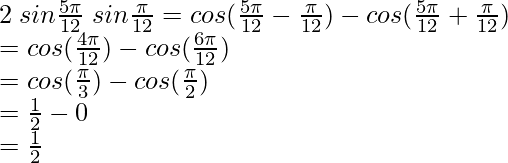
Hence, LHS = RHS
(ii) 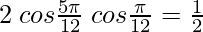
Solution:
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
Taking A =  and B =
and B = 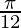
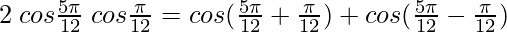
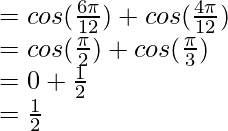
Hence, LHS = RHS
(iii) 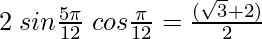
Solution:
By using the trigonometric identity,
2 sin A cos B = sin (A+B) + sin (A-B)
Taking A =  and B =
and B = 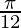
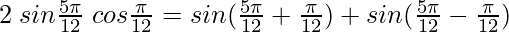
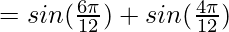
= sin 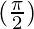 + sin
+ sin 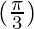
= 1 + 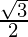
= 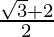
Hence, LHS = RHS
Question 3. Show that:
(i) sin 50° cos 85° = 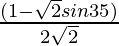
Solution:
By using the trigonometric identity,
2 sin A cos B = sin (A+B) + sin (A-B)
sin A cos B =  (sin (A+B) + sin (A-B))
(sin (A+B) + sin (A-B))
Taking A = 50° and B = 85°
sin 50° cos 85° =  (sin (50°+85°) + sin (50°-85°))
(sin (50°+85°) + sin (50°-85°))
=  (sin (135°) + sin (-35°))
(sin (135°) + sin (-35°))
=  (sin (180°-45°) – sin (35°)) (sin(-θ)=-sin θ)
(sin (180°-45°) – sin (35°)) (sin(-θ)=-sin θ)
=  (sin (45°) – sin (35°)) (sin(π-θ)=sin θ)
(sin (45°) – sin (35°)) (sin(π-θ)=sin θ)

Hence, LHS = RHS
(ii) sin 25° cos 115° = 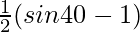
Solution:
By using the trigonometric identity,
2 sin A cos B = sin (A+B) + sin (A-B)
sin A cos B =  (sin (A+B) + sin (A-B))
(sin (A+B) + sin (A-B))
Taking A = 25° and B = 115°
sin 25° cos 115° =  (sin (25°+85°) + sin (25°-115°))
(sin (25°+85°) + sin (25°-115°))
=  (sin (140°) + sin (-90°))
(sin (140°) + sin (-90°))
=  (sin (180-40°) – sin (90°)) (sin(-θ)=-sin θ)
(sin (180-40°) – sin (90°)) (sin(-θ)=-sin θ)
=  (sin (40°) – sin (90°)) (sin(π-θ)=sin θ)
(sin (40°) – sin (90°)) (sin(π-θ)=sin θ)
=  (sin (40°) – 1)
(sin (40°) – 1)
Hence, LHS = RHS
Question 4. Prove that : 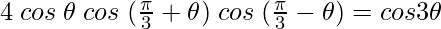
Solution:
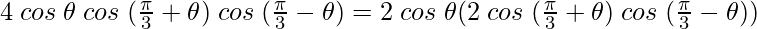
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
Taking A = 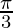 +θ and B =
+θ and B = 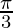 -θ
-θ
![Rendered by QuickLaTeX.com = 2 \hspace{0.1cm}cos \hspace{0.1cm}\theta(cos\hspace{0.1cm} (\frac{\pi}{3} + \theta+\frac{\pi}{3} - \theta) +cos\hspace{0.1cm} (\frac{\pi}{3} + \theta)-(\frac{\pi}{3} - \theta))\\ = 2 \hspace{0.1cm}cos \hspace{0.1cm}\theta(cos\hspace{0.1cm} (\frac{2\pi}{3}) +cos\hspace{0.1cm} (2\theta))\\ = 2 \hspace{0.1cm}cos \hspace{0.1cm}\theta(cos\hspace{0.1cm} (\pi+\frac{\pi}{3}) +cos\hspace{0.1cm} (2\theta))\\ = 2 \hspace{0.1cm}cos \hspace{0.1cm}\theta(- cos\hspace{0.1cm} (\frac{\pi}{3}) +cos\hspace{0.1cm} (2\theta))\\ = 2 \hspace{0.1cm}cos \hspace{0.1cm}\theta(- \frac{1}{2} +cos\hspace{0.1cm} (2\theta))\\ = - cos \hspace{0.1cm}\theta + [2 \hspace{0.1cm}cos \hspace{0.1cm}\theta\hspace{0.1cm} cos\hspace{0.1cm} (2\theta))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3808af58ec97517460326d5c0219e172_l3.png)
Using the identity again, we have
Taking A = 2θ and B = θ
![Rendered by QuickLaTeX.com = - cos \hspace{0.1cm}\theta + [cos\hspace{0.1cm} (2\theta + \theta) +cos\hspace{0.1cm} (2\theta - \theta)]\\ = - cos \hspace{0.1cm}\theta + cos\hspace{0.1cm} (3\theta) +cos\hspace{0.1cm} (\theta)\\ = cos\hspace{0.1cm} (3\theta)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-56075c49f8924c2f51e093579d233230_l3.png)
Hence, LHS = RHS
Question 5. Prove that :
(i) cos 10° cos 30° cos 50° cos 70° = 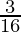
Solution:
cos 10° cos 30° cos 50° cos 70° = cos 30° cos 10° cos 50° cos 70°
= 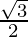 (cos 10° cos 50°) cos 70°
(cos 10° cos 50°) cos 70°
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
cos A cos B =  [cos (A+B) + cos (A-B)]
[cos (A+B) + cos (A-B)]
Taking A = 10° and B = 50°
= 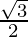 (
( [cos (10°+50°) + cos (10°-50°)]) cos 70°
[cos (10°+50°) + cos (10°-50°)]) cos 70°
= 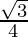 (cos (60°) + cos (-40°)) cos 70°
(cos (60°) + cos (-40°)) cos 70°
= 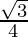 (
( + cos (40°)) cos 70°
+ cos (40°)) cos 70°
= 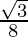 cos 70° +
cos 70° + 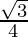 (cos 70° cos (40°))
(cos 70° cos (40°))
Again using the identity, we get
= 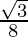 cos 70° +
cos 70° + 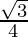 (
( [cos (70°+40°) + cos (70°-40°)])
[cos (70°+40°) + cos (70°-40°)])
= 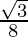 cos 70° +
cos 70° + 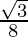 [cos (110°) + cos (30°)]
[cos (110°) + cos (30°)]
= 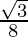 cos 70° +
cos 70° + 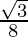 [cos (110°) +
[cos (110°) + 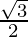 ]
]
= 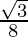 cos 70° +
cos 70° + 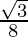 cos (110°) +
cos (110°) + 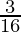
= 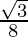 (cos 70° + cos (110°)) +
(cos 70° + cos (110°)) + 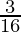
= 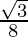 (cos 70° + cos (180°-70°)) +
(cos 70° + cos (180°-70°)) + 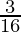
= 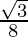 (cos 70° – cos (70°)) +
(cos 70° – cos (70°)) + 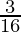
= 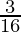
Hence, LHS = RHS
(ii) cos 40° cos 80° cos 160° = 
Solution:
cos 40° cos 80° cos 160° = cos 80° (cos 40° cos 160°)
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
cos A cos B =  [cos (A+B) + cos (A-B)]
[cos (A+B) + cos (A-B)]
Taking A = 160° and B = 40°
= cos 80° ( [cos (160°+40°) + cos (160°-40°)])
[cos (160°+40°) + cos (160°-40°)])
= cos 80° ( [cos (200°) + cos (120°)])
[cos (200°) + cos (120°)])
= cos 80° ( [cos (180°+20°) + cos (180°-60°)])
[cos (180°+20°) + cos (180°-60°)])
= cos 80° ( [- cos (20°) + (-cos (60°))])
[- cos (20°) + (-cos (60°))])
= cos 80° ( [- cos (20°) – cos (60°)])
[- cos (20°) – cos (60°)])
= cos 80° ( [- cos (20°) –
[- cos (20°) –  ])
])
= 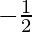 (cos 80° cos (20°) +
(cos 80° cos (20°) +  cos 80°])
cos 80°])
Again using the identity, we get
![Rendered by QuickLaTeX.com = -\frac{1}{2} ((\frac{1}{2}[cos (80\degree+20\degree) + cos (80\degree-20\degree)]) + \frac{1}{2} cos 80\degree)\\ = -\frac{1}{4} ((cos (100\degree) + cos (60\degree)) + cos 80\degree)\\ = -\frac{1}{4} (cos (180\degree-80\degree) + cos (60\degree) + cos 80\degree)\\ = -\frac{1}{4} (- cos (80\degree) + cos (60\degree) + cos 80\degree)\\ = -\frac{1}{4} (cos (60\degree))\\ = -\frac{1}{4} (\frac{1}{2})\\ = -\frac{1}{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-15952c803aaa885f432ffb4c98f3f86f_l3.png)
Hence, LHS = RHS
(iii) sin 20° sin 40° sin 80° = 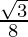
Solution:
sin 20° sin 40° sin 80° = (sin 20° sin 40°) sin 80°
By using the trigonometric identity,
2 sin A sin B = cos (A-B) – cos (A+B)
sin A sin B =  [cos (A-B) – cos (A+B)]
[cos (A-B) – cos (A+B)]
Taking A = 40° and B = 20°
= ( [cos (40°-20°) – cos (40°+20°)]) sin 80°
[cos (40°-20°) – cos (40°+20°)]) sin 80°
=  sin 80° [cos (20°) – cos (60°)]
sin 80° [cos (20°) – cos (60°)]
=  sin 80° [cos (20°) –
sin 80° [cos (20°) –  ]
]
=  [sin 80° cos (20°) –
[sin 80° cos (20°) –  sin 80°]
sin 80°]
By using the trigonometric identity,
2 sin A cos B = sin (A+B) + sin (A-B)
sin A cos B =  [sin (A+B) + sin (A-B)]
[sin (A+B) + sin (A-B)]
Taking A = 80° and B = 20°
![Rendered by QuickLaTeX.com = \frac{1}{2} [(\frac{1}{2}[sin (80\degree+20\degree) + sin (80\degree-20\degree)]) - \frac{1}{2} sin 80\degree]\\ = \frac{1}{4} [(sin (80\degree+20\degree) + sin (80\degree-20\degree)) - sin 80\degree]\\ = \frac{1}{4} [sin (100\degree) + sin (60\degree) - sin 80\degree]\\ = \frac{1}{4} [sin (180\degree-80\degree) + \frac{\sqrt{3}}{2} - sin 80\degree]\\ = \frac{1}{4} [sin (80\degree) + \frac{\sqrt{3}}{2} - sin 80\degree]\\ = \frac{1}{4} [\frac{\sqrt{3}}{2}]\\ = \frac{\sqrt{3}}{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-435179a46730b54cbd6480457be12279_l3.png)
Hence, LHS = RHS
(iv) cos 20° cos 40° cos 80° = 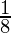
Solution:
cos 20° cos 40° cos 80° = cos 40° (cos 20° cos 80°)
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
cos A cos B =  [cos (A+B) + cos (A-B)]
[cos (A+B) + cos (A-B)]
Taking A = 80° and B = 20°
![Rendered by QuickLaTeX.com = cos 40\degree (\frac{1}{2}[cos (80\degree+20\degree) + cos (80\degree-20\degree)])\\ = \frac{1}{2} cos 40\degree [cos (100\degree) + cos (60\degree)]\\ = \frac{1}{2} cos 40\degree[cos (180\degree-80\degree) + cos (60\degree)]\\ = \frac{1}{2} cos 40\degree [- cos (80\degree) + \frac{1}{2}]\\ = \frac{1}{2} cos 40\degree [\frac{1}{2}- cos (80\degree)]\\ = \frac{1}{2} [\frac{1}{2} cos 40\degree - cos (80\degree) cos 40\degree]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b885a73729dadc927c9064ac69d217be_l3.png)
Again using the identity, we get
![Rendered by QuickLaTeX.com = \frac{1}{2} [\frac{1}{2} cos 40\degree - \frac{1}{2}(cos (80\degree+40\degree) + cos (80\degree-40\degree))]\\ = \frac{1}{2} [\frac{1}{2} cos 40\degree - \frac{1}{2}(cos (120\degree) + cos (40\degree))]\\ = \frac{1}{2} [\frac{1}{2} cos 40\degree - \frac{1}{2}(cos (180\degree-60\degree) + cos (40\degree))]\\ = \frac{1}{2} [\frac{1}{2} cos 40\degree - \frac{1}{2}(- cos (60\degree) + cos (40\degree))]\\ = \frac{1}{2} [\frac{1}{2} cos 40\degree + \frac{1}{2} cos (60\degree) - \frac{1}{2} cos (40\degree)]\\ = \frac{1}{2} [\frac{1}{2} \frac{1}{2}]\\ = \frac{1}{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b22e386c3cd429910b7d76cc7194229f_l3.png)
Hence, LHS = RHS
(v) tan 20° tan 40° tan 60° tan 80° = 3
Solution:
tan 20° tan 40° tan 60° tan 80° = tan 60° 
= 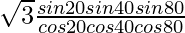
= 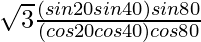
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
cos A cos B =  [cos (A+B) + cos (A-B)]
[cos (A+B) + cos (A-B)]
and, 2 sin A sin B = cos (A-B) – cos (A+B)
sin A sin B =  [cos (A-B) – cos (A+B)]
[cos (A-B) – cos (A+B)]
Taking A = 40° and B = 20°
![Rendered by QuickLaTeX.com = \sqrt{3} (\frac{(\frac{1}{2}[cos ( 40\degree- 20\degree) - cos ( 40\degree+ 20\degree)]) sin 80\degree}{(\frac{1}{2}[cos ( 40\degree+ 20\degree) + cos ( 40\degree- 20\degree)]) cos 80\degree})\\ = \sqrt{3} (\frac{[cos ( 20\degree) - cos (60\degree)] sin 80\degree}{([cos ( 60\degree) + cos (20\degree)) cos 80\degree})\\ = \sqrt{3} (\frac{[cos ( 20\degree) - \frac{1}{2}] sin 80\degree}{(\frac{1}{2} + cos (20\degree)) cos 80\degree})\\ = \sqrt{3} (\frac{(cos ( 20\degree) sin 80\degree - \frac{1}{2} sin 80\degree)}{\frac{1}{2} cos 80\degree + cos (20\degree) cos 80\degree})\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f2ad819ae9769c8234fd4fb2defbf665_l3.png)
Again using the identity, we get
2 sin A cos B = sin (A+B) + sin (A-B)
sin A cos B =  [sin (A+B) + sin (A-B)]
[sin (A+B) + sin (A-B)]
Taking A = 80° and B = 20°
![Rendered by QuickLaTeX.com = \sqrt{3} (\frac{(\frac{1}{2}[sin (80\degree+20\degree) + sin (80\degree-20\degree)] - \frac{1}{2} sin 80\degree)}{\frac{1}{2} cos 80\degree + \frac{1}{2}[cos (80\degree+20\degree) + cos (80\degree-20\degree)]})\\ = \sqrt{3} (\frac{(\frac{1}{2}[sin (100\degree) + sin (60\degree)] - \frac{1}{2} sin 80\degree)}{\frac{1}{2} cos 80\degree + \frac{1}{2}[cos (100\degree) + cos (60\degree)]})\\ = \sqrt{3} (\frac{(\frac{1}{2}[sin (180\degree-80\degree) + sin (60\degree)] - \frac{1}{2} sin 80\degree)}{\frac{1}{2} cos 80\degree + \frac{1}{2}[cos (180\degree-80\degree) + cos (60\degree)]})\\ = \sqrt{3} (\frac{(\frac{1}{2} sin (80\degree) + \frac{1}{2} sin (60\degree) - \frac{1}{2} sin 80\degree)}{\frac{1}{2} (- cos 80\degree) + \frac{1}{2} cos (80\degree) + \frac{1}{2} cos (60\degree)})\\ = \sqrt{3} (\frac{(\frac{1}{2} sin (60\degree)}{\frac{1}{2} cos (60\degree)})\\ = \sqrt{3} (tan (60\degree))\\ = \sqrt{3} (\sqrt{3})\\ = 3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-705f2aaf0defeda4be87e34ceaa05c22_l3.png)
Hence, LHS = RHS
(vi) tan 20° tan 30° tan 40° tan 80° = 1
Solution:
tan 20° tan 30° tan 40° tan 80° = tan 30° 
= 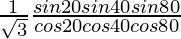
= 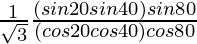
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
cos A cos B =  [cos (A+B) + cos (A-B)]
[cos (A+B) + cos (A-B)]
and, 2 sin A sin B = cos (A-B) – cos (A+B)
sin A sin B =  [cos (A-B) – cos (A+B)]
[cos (A-B) – cos (A+B)]
Taking A = 40° and B = 20°
![Rendered by QuickLaTeX.com = \frac{1}{\sqrt{3}}\frac{(\frac{1}{2}[cos ( 40\degree- 20\degree) - cos ( 40\degree+ 20\degree)]) sin 80\degree}{(\frac{1}{2}[cos ( 40\degree+ 20\degree) + cos ( 40\degree- 20\degree)]) cos 80\degree}\\ = \frac{1}{\sqrt{3}}\frac{[cos ( 20\degree) - cos (60\degree)] sin 80\degree}{([cos ( 60\degree) + cos (20\degree)) cos 80\degree}\\ = \frac{1}{\sqrt{3}} \frac{[cos ( 20\degree) - \frac{1}{2}] sin 80\degree}{(\frac{1}{2}+ cos (20\degree)) cos 80\degree}\\ = \frac{1}{\sqrt{3}} \frac{(cos ( 20\degree) sin 80\degree - \frac{1}{2}sin 80\degree)}{\frac{1}{2} cos 80\degree + cos (20\degree) cos 80\degree}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35f2fd88a56c80969ca58990f8afc09e_l3.png)
Again using the identity, we get
2 sin A cos B = sin (A+B) + sin (A-B)
sin A cos B = \frac{1}{2}[sin (A+B) + sin (A-B)]
Taking A = 80° and B = 20°
![Rendered by QuickLaTeX.com = \frac{1}{\sqrt{3}} (\frac{1}{2}[sin (80\degree+20\degree) + sin (80\degree-20\degree)] - \frac{1}{2} sin 80\degree){\frac{1}{2} cos 80\degree + \frac{1}{2}[cos (80\degree+20\degree) + cos (80\degree-20\degree)]}\\ = \frac{1}{\sqrt{3}} (\frac{1}{2}[sin (100\degree) + sin (60\degree)] - \frac{1}{2} sin 80\degree){\frac{1}{2} cos 80\degree + \frac{1}{2}[cos (100\degree) + cos (60\degree)]}\\ = \frac{1}{\sqrt{3}} (\frac{1}{2}[sin (180\degree-80\degree) + sin (60\degree)] - \frac{1}{2} sin 80\degree){\frac{1}{2} cos 80\degree + \frac{1}{2}[cos (180\degree-80\degree) + cos (60\degree)]}\\ = \frac{1}{\sqrt{3}} (\frac{1}{2} sin (80\degree) + \frac{1}{2} sin (60\degree) - \frac{1}{2} sin 80\degree){\frac{1}{2} (- cos 80\degree) + \frac{1}{2} cos (80\degree) + \frac{1}{2} cos (60\degree)}\\ = \frac{1}{\sqrt{3}} (\frac{1}{2} sin (60\degree){\frac{1}{2} cos (60\degree)}\\ = \frac{1}{\sqrt{3}} (tan (60\degree))\\ = \frac{1}{\sqrt{3}} (\sqrt{3})\\ = 1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a22e2f88eb2d8336dda90a77faabed04_l3.png)
Hence, LHS = RHS
(vii) sin 10° sin 50° sin 60° sin 70° = 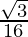
Solution:
sin 10° sin 50° sin 60° sin 70° = sin 60° (sin 10° sin 50° sin 70°)
= \frac{\sqrt{3}}{2} (sin (90-80°) sin (90-40°) sin (90-20°))
= 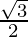 (cos (80°) cos (40°) cos (20°))
(cos (80°) cos (40°) cos (20°))
= 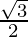 cos 40° (cos 80° cos 20°)
cos 40° (cos 80° cos 20°)
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
cos A cos B =  [cos (A+B) + cos (A-B)]
[cos (A+B) + cos (A-B)]
Taking A = 80° and B = 20°
![Rendered by QuickLaTeX.com = \frac{\sqrt{3}}{2} cos 40\degree (\frac{1}{2}[cos (80\degree+20\degree) + cos (80\degree-20\degree)])\\ = \frac{\sqrt{3}}{2} \frac{1}{2} cos 40\degree [cos (100\degree) + cos (60°)]\\ = \frac{\sqrt{3}}{4} cos 40\degree[cos (180\degree-80\degree) + cos (60\degree)]\\ = \frac{\sqrt{3}}{4} cos 40\degree [- cos (80\degree) + \frac{1}{2}]\\ = \frac{\sqrt{3}}{4} cos 40\degree [\frac{1}{2}- cos (80\degree)]\\ = \frac{\sqrt{3}}{4} [\frac{1}{2} cos 40\degree - cos (80\degree) cos 40\degree]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a644e85ac0580363f727e74b16048fb7_l3.png)
Again using the identity, we get
![Rendered by QuickLaTeX.com = \frac{\sqrt{3}}{4} [\frac{1}{2} cos 40\degree - \frac{1}{2}(cos (80\degree+40\degree) + cos (80\degree-40\degree))]\\ = \frac{\sqrt{3}}{4} [\frac{1}{2} cos 40\degree - \frac{1}{2}(cos (120\degree) + cos (40\degree))]\\ = \frac{\sqrt{3}}{4} [\frac{1}{2} cos 40\degree - \frac{1}{2}(cos (180\degree-60\degree) + cos (40\degree))]\\ = \frac{\sqrt{3}}{4} [\frac{1}{2} cos 40\degree - \frac{1}{2}(- cos (60\degree) + cos (40\degree))]\\ = \frac{\sqrt{3}}{4} [\frac{1}{2} cos 40\degree + \frac{1}{2} cos (60\degree) - \frac{1}{2} cos (40\degree)]\\ = \frac{\sqrt{3}}{4} [\frac{1}{2} \frac{1}{2}]\\ = \frac{\sqrt{3}}{16}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-22197789d02a17cd44e5606932a79086_l3.png)
Hence, LHS = RHS
(viii) sin 20° sin 40° sin 60° sin 80° = 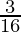
Solution:
sin 20° sin 40° sin 60° sin 80° = sin 60° (sin 20° sin 40° sin 80°)
=  (sin 20° sin 40°) sin 80°
(sin 20° sin 40°) sin 80°
By using the trigonometric identity,
2 sin A sin B = cos (A-B) – cos (A+B)
sin A sin B =  [cos (A-B) – cos (A+B)]
[cos (A-B) – cos (A+B)]
Taking A = 40° and B = 20°
![Rendered by QuickLaTeX.com = \frac{\sqrt{3}}{2} (\frac{1}{2}[cos (40\degree-20\degree) - cos (40\degree+20\degree)]) sin 80\degree\\ = \frac{\sqrt{3}}{2} \frac{1}{2} sin 80\degree [cos (20\degree) - cos (60\degree)]\\ = \frac{\sqrt{3}}{4} sin 80\degree [cos (20\degree) - \frac{1}{2}]\\ = \frac{\sqrt{3}}{4} [sin 80\degree cos (20\degree) - \frac{1}{2} sin 80\degree]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d593df109ea3d3c123f8489a075dc55_l3.png)
By using the trigonometric identity,
2 sin A cos B = sin (A+B) + sin (A-B)
sin A cos B =  [sin (A+B) + sin (A-B)]
[sin (A+B) + sin (A-B)]
Taking A = 80° and B = 20°
![Rendered by QuickLaTeX.com = \frac{\sqrt{3}}{4} [(\frac{1}{2}[sin (80\degree+20\degree) + sin (80\degree-20\degree)]) - \frac{1}{2} sin 80\degree]\\ = \frac{\sqrt{3}}{8} [(sin (80\degree+20\degree) + sin (80\degree-20\degree)) - sin 80\degree]\\ = \frac{\sqrt{3}}{8} [sin (100\degree) + sin (60\degree) - sin 80\degree]\\ = \frac{\sqrt{3}}{8} [sin (180\degree-80\degree) + \frac{\sqrt{3}}{2} - sin 80\degree]\\ = \frac{\sqrt{3}}{8} [sin (80\degree) + \frac{\sqrt{3}}{2} - sin 80\degree]\\ = \frac{\sqrt{3}}{8} [\frac{\sqrt{3}}{2}]\\ = \frac{3}{16}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d4372a5a0c4aec3ffc206d74bb0a0f50_l3.png)
Hence, LHS = RHS
Question 6. Show that
(i) sin A sin (B-C) + sin B sin (C-A) + sin C sin (A-B) = 0
Solution:
By using the trigonometric identity,
2 sin θ sin Φ = cos (θ-Φ) – cos (θ+Φ)
sin θ sin Φ =  [cos (θ-Φ) – cos (θ+Φ)]
[cos (θ-Φ) – cos (θ+Φ)]
sin A sin (B-C) + sin B sin (C-A) + sin C sin (A-B) = ( [cos (A-(B-C)) – cos (A+(B-C))]) + (
[cos (A-(B-C)) – cos (A+(B-C))]) + ( [cos (B-(C-A)) – cos (B+(C-A))]) + (
[cos (B-(C-A)) – cos (B+(C-A))]) + ( [cos (C-(A-B)) – cos (C+(A-B))])
[cos (C-(A-B)) – cos (C+(A-B))])
=  (cos (A-B+C)) – cos (A+B-C) + cos (B-C+A) – cos (B+C-A) + cos (C-A+B) – cos (C+A-B))
(cos (A-B+C)) – cos (A+B-C) + cos (B-C+A) – cos (B+C-A) + cos (C-A+B) – cos (C+A-B))
=  (cos (A-B+C)) – cos (C+A-B) – cos (A+B-C) + cos (B-C+A) – cos (B+C-A) + cos (C-A+B))
(cos (A-B+C)) – cos (C+A-B) – cos (A+B-C) + cos (B-C+A) – cos (B+C-A) + cos (C-A+B))
= 
= 0
Hence, LHS = RHS
(ii) sin (B-C) cos (A-D) + sin (C-A) cos (B-D) + sin (A-B) cos (C-D) = 0
Solution:
By using the trigonometric identity,
2 sin θ cos Φ = sin (θ+Φ) + sin (θ-Φ)
sin θ cos Φ =  [sin (θ+Φ) + sin (θ-Φ)]
[sin (θ+Φ) + sin (θ-Φ)]
sin (B-C) cos (A-D) + sin (C-A) cos (B-D) + sin (A-B) cos (C-D) = ( [sin (B-C+(A-D)) + sin (B-C-(A-D))]) + (
[sin (B-C+(A-D)) + sin (B-C-(A-D))]) + ( [sin (C-A+(B-D)) + sin (C-A-(B-D))]) +(
[sin (C-A+(B-D)) + sin (C-A-(B-D))]) +( [sin (A-B+(C-D)) + sin (A-B-(C-D))])
[sin (A-B+(C-D)) + sin (A-B-(C-D))])
= ( [sin (A+B-C-D) + sin (-A+B-C+D)]) + (
[sin (A+B-C-D) + sin (-A+B-C+D)]) + ( [sin (-A+B+C-D) + sin (-A-B+C+D)]) +(
[sin (-A+B+C-D) + sin (-A-B+C+D)]) +( [sin (A-B+C-D) + sin (A-B-C+-D)])
[sin (A-B+C-D) + sin (A-B-C+-D)])
=  (sin (A+B-C-D) + sin (-(A-B+C-D)) + sin (-(A-B-C+D)) + sin (-(A+B-C-D)) +sin (A-B+C-D) + sin (A-B-C+-D))
(sin (A+B-C-D) + sin (-(A-B+C-D)) + sin (-(A-B-C+D)) + sin (-(A+B-C-D)) +sin (A-B+C-D) + sin (A-B-C+-D))
=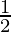 (sin (A+B-C-D) – sin(A-B+C-D) – sin (A-B-C+D) – sin (A+B-C-D) +sin (A-B+C-D) + sin (A-B-C+-D))
(sin (A+B-C-D) – sin(A-B+C-D) – sin (A-B-C+D) – sin (A+B-C-D) +sin (A-B+C-D) + sin (A-B-C+-D))
= 
= 0
Hence, LHS = RHS
Question 7. Prove that : tan θ tan (60°-θ) tan (60°+θ) = tan 3θ
Solution:
tan θ tan (60°-θ) tan (60°+θ) = tan θ (tan (60°-θ)) (tan (60°+θ))
By using the trigonometric identity,
tan (a+b) = 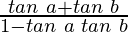
tan (a+b) = 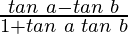
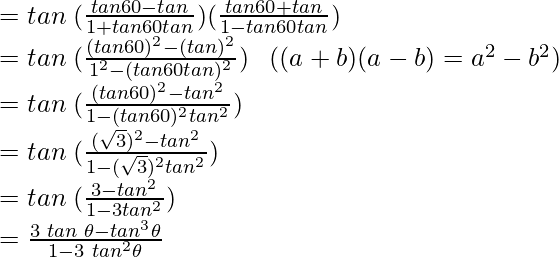
= tan 3θ
Hence, LHS = RHS
Question 8. If α + β = 90°, show that the maximum value of cos(α) cos(β) is 
Solution:
cos(α) cos(β) = y
By using the trigonometric identity,
2 cos A cos B = cos (A+B) + cos (A-B)
cos A cos B =  [cos (A+B) + cos (A-B)]
[cos (A+B) + cos (A-B)]
Taking A = α and B = β
cos(α) cos(β) =  [cos (α+β) + cos (α-β)]
[cos (α+β) + cos (α-β)]
As, α + β = 90°
y =  [cos (90°) + cos (α-β)]
[cos (90°) + cos (α-β)]
y =  [0 + cos (α-β)]
[0 + cos (α-β)]
y =  (cos (α-β))
(cos (α-β))
AS, we know that range of cos function is [-1,1]
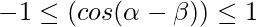
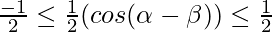
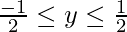
Hence, the maximum value of cos(α) cos(β) is 
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...