Class 11 RD Sharma Solutions – Chapter 10 Sine and Cosine Formulae and Their Applications – Exercise 10.1 | Set 1
Last Updated :
16 May, 2021
Question 1: If in △ABC, ∠A=45°, ∠B=60°, and ∠C=75°, find the ratio of its sides.
Solution:
According to the sine rule

Hence, we get
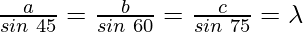
Using the formula,
sin (A+B) = sin A cos B + cos A sin B
sin (45°+30°) = sin(45°) cos(30°) + cos(45°) sin(30°)
sin 75° =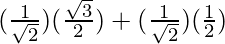
sin 75° =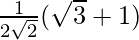
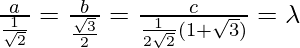
Multiplying the denominator by 2√2, we get
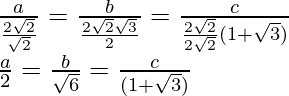
Hence, we get
a : b : c = 2 : √6 : (√3+1)
Question 2: If in △ABC, ∠C=105°, ∠B=45°, and a=2, then find b.
Solution:
In the given condition, ∠C=105° and ∠B=45°
And as we know that,
A+B+C = π (Sum of all angles in triangle is supplementary)
A = π-(B+C)
A = 180°-(45°+105°)
A = 30°
Now, according the sine rule
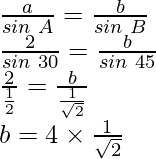
After rationalizing the denominator, we get
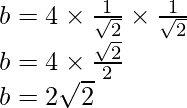
Question 3: In △ABC, if a=18, b=24, and c=30 and ∠C=90°, find sin A, sin B, and sin C.
Solution:
In the given condition, a=18, b=24 and c=30 and ∠C=90°
Now, according the sine rule
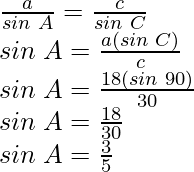
Also,
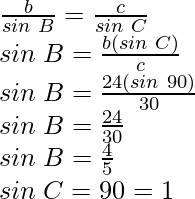
Question 4: In △ABC, prove the following:
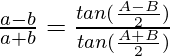
Solution:
According to the sine rule

Considering the LHS of the equation, we have
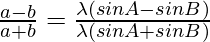
By using trigonometric formula,
sin A – sin B = 2 sin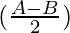 cos
cos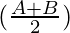
sin A + sin B = 2 sin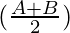 cos
cos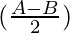
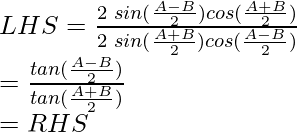
As, LHS = RHS
Hence, proved !!
Question 5: In △ABC, prove the following:
(a-b)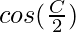 = c
= c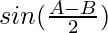
Solution:
According to the sine rule

Considering LHS, we have
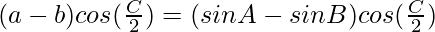
By using trigonometric formula,
sin A – sin B = 2 sin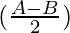 cos
cos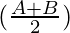
= λ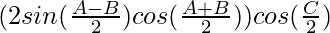
A+B+C = π (Sum of all angles in triangle is supplementary)
= 2λ sin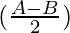 cos
cos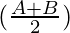 cos
cos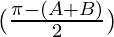
= 2λ sin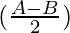 cos
cos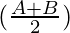 cos
cos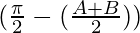
= λ sin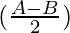 (2cos
(2cos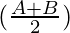 sin
sin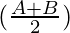 )
)
By using trigonometric formula,
2 sin a cos a = sin 2a
= λ sin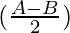 (sin
(sin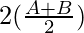 )
)
= λ sin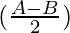 sin(A+B)
sin(A+B)
= λ sin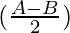 sin(π-C) (A+B+C = π)
sin(π-C) (A+B+C = π)
= λ sin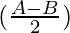 sin(C)
sin(C)
= (λ sin C) sin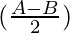
= c sin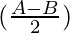
As, LHS = RHS
Hence Proved!
Question 6: In △ABC, prove the following:
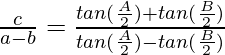
Solution:
According to the sine rule

Considering LHS, we have
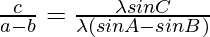
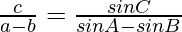
By using trigonometric identities,
sin A – sin B = 2 sin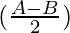 cos
cos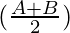
sin 2a = 2 sin a cos a
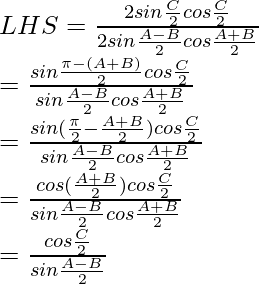 ……………………….(1)
……………………….(1)
Now considering RHS, we have
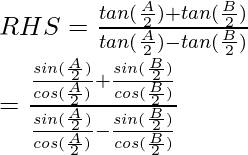
Cross multiplying we get,
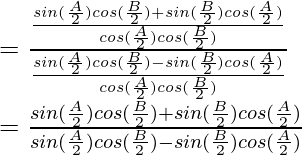
By using trigonometric identities,
sin a cos b + cos a sin b = sin (a+b)
sin a cos b – cos a sin b = sin (a-b)
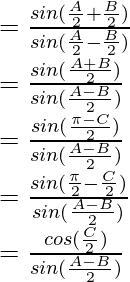 ……………………….(2)
……………………….(2)
As, LHS = RHS
Hence Proved!
Question 7: In △ABC, prove the following:
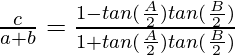
Solution:
According to the sine rule

Considering LHS, we have
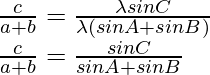
By using trigonometric identities,
sin A + sin B = 2 sin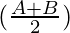 cos
cos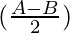
sin 2a = 2 sin a cos a
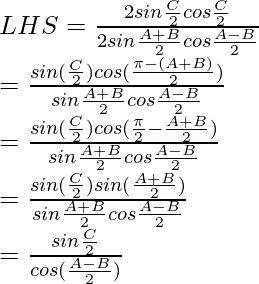 ………………………….(1)
………………………….(1)
Now considering RHS, we have
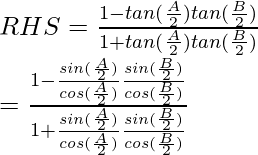
Cross multiplying we get,
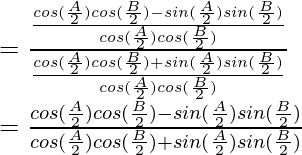
By using trigonometric identities,
cos a cos b + sin a sin b = cos (a-b)
cos a cos b – sin a sin b = cos (a+b)
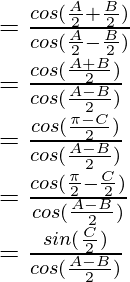 ……………………….(2)
……………………….(2)
As, LHS = RHS
Hence, Proved!
Question 8: In △ABC, prove the following:
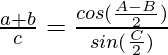
Solution:
According to the sine rule

Considering LHS, we have
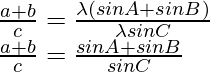
By using trigonometric identities,
sin A + sin B = 2 sin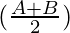 cos
cos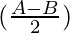
sin 2a = 2 sin a cos a
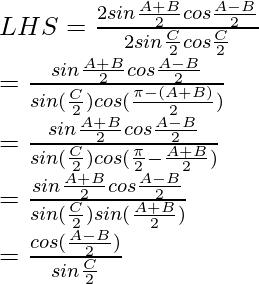
As, LHS = RHS
Hence, Proved!
Question 9: In △ABC, prove the following:
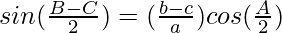
Solution:
According to the sine rule

Considering RHS, we have
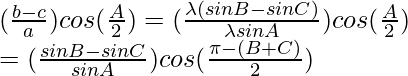
By using trigonometric identities,
sin A – sin B = 2 sin cos
cos
![Rendered by QuickLaTeX.com LHS = (\frac{2 sin\frac{B-C}{2}cos\frac{B+C}{2}}{sinA})cos(\frac{\pi}{2}-\frac{B+C}{2})\\ = (\frac{2 sin\frac{B-C}{2}cos\frac{B+C}{2}}{sinA})sin(\frac{B+C}{2})\\ = (\frac{[2 sin(\frac{B+C}{2}) cos\frac{B+C}{2}] sin\frac{B-C}{2}}{sinA})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3a360aa93c71492a15cf71f8c765d64_l3.png)
By using trigonometric identities,
2 sin a cos a = sin 2a
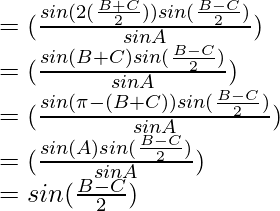
As, LHS = RHS
Hence, Proved!
Question 10: In △ABC, prove the following:
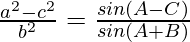
Solution:
According to the sine rule

Considering LHS, we have
![Rendered by QuickLaTeX.com \frac{a^2-c^2}{b^2} = \frac{[\lambda sinA]^2-[\lambda sinC]^2}{[\lambda sinB]^2}\\ = \frac{(\lambda)^2 [sin^2A - sin^2C]}{(\lambda)^2[sin^2B]}\\ = \frac{sin^2A - sin^2C}{sin^2B}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bed56f4cd4175f0ba69d5daa527633fe_l3.png)
By using trigonometric identities,
sin2 a – sin2 b = sin(a+b) sin (a-b)
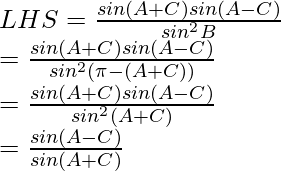
As, LHS = RHS
Hence, Proved!
Question 11: In △ABC, prove the following:
b sin B – c sin C = a sin (B-C)
Solution:
According to the sine rule

And, cosine rule,
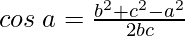
Considering RHS, we have
RHS = a sin (B-C)
By using trigonometric identities,
sin(a-b) = sin a cos b – cos a sin b
= a (sin B cos C – cos B sin C)
= a ((bλ)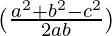 –
–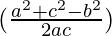 (cλ))
(cλ))
= λ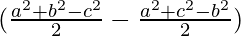
= 2λ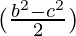
= λb2-λc2
= b(λb) – c(λc)
= b(sin B) – c(cos C)
As, LHS = RHS
Hence, Proved!
Question 12: In △ABC, prove the following:
a2 sin (B-C) = (b2-c2) sin A
Solution:
According to the sine rule

Considering RHS, we have
RHS = (b2-c2) sin A
= λ2 sin A(sin2 B – sin2 C)
By using trigonometric identities,
sin2 a – sin2 b = sin(a+b) sin (a-b)
= λ2 sin A(sin(B+C) sin (B-C))
= λ2 sin A(sin(\pi-A) sin (B-C))
= λ2 sin A(sin(A) sin (B-C))
= λ2 sin2 A sin (B-C)
= (λ sin A)2 sin (B-C)
= a2 sin (B-C)
As, LHS = RHS
Hence, Proved!
Question 13: In △ABC, prove the following:
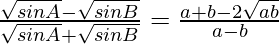
Solution:
Considering LHS, we have
LHS =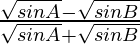
Rationalizing the denominator, we get
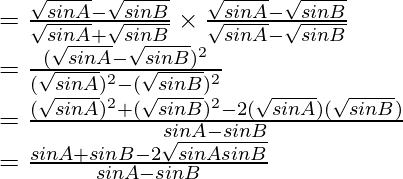
According to the sine rule

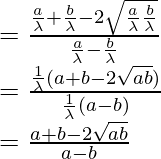
As, LHS = RHS
Hence, Proved!
Question 14: In △ABC, prove the following:
a (sin B – sin C) + b(sin C – sin A) + c(sin A – sin B) = 0
Solution:
According to the sine rule

Considering LHS, we have
LHS = a (sin B – sin C) + b(sin C – sin A) + c(sin A – sin B)
= λ sin A (sin B – sin C) + λ sin B (sin C – sin A) + λ sin C (sin A – sin B)
= λ sin A sin B – λ sin A sin C + λ sin B sin C – λ sin B sin A) + λ sin C sin A – λ sin C sin B
= 0
As, LHS = RHS
Hence, Proved!
Question 15: In △ABC, prove the following:
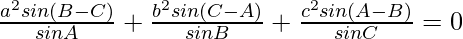
Solution:
According to the sine rule

Considering LHS, we have
LHS =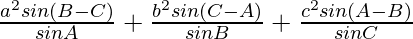
=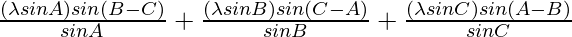
= λ2 sin A sin (B-C) + λ2 sin B sin (C-A) + λ2 sin C sin (A-B)
By using trigonometric identities,
sin(a-b) = sin a cos b – cos a sin b
= λ2 (sin A [sin B cos C – cos B sin C] + sin B [sin C cos A – cos C sin A] + sin C [sin A cos B – cos A sin B])
= λ2 (sin A sin B cos C – sin A cos B sin C + sin B sin C cos A – sin B cos C sin A + sin C sin A cos B – sin C cos A sin B)
= λ2 (0)
= 0
As, LHS = RHS
Hence, Proved!
Share your thoughts in the comments
Please Login to comment...