Class 11 RD Sharma Solutions – Chapter 5 Trigonometric Functions – Exercise 5.1 | Set 2
Last Updated :
21 Feb, 2021
Question 14. Prove that 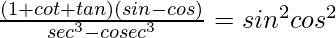
Solution:
We have
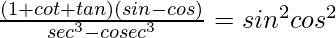
Taking LHS
= 
= 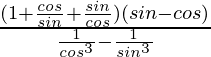
= 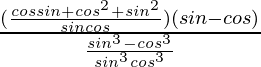
= 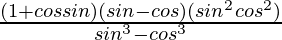
= 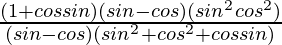
= 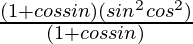
= sin2θcos2θ
Hence, LHS = RHS (Proved)
Question 15. Prove that 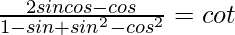
Solution:
We Have
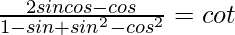
Taking LHS
= 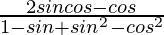
= 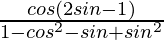
= 
= 
= 
= cosθ/sinθ
= cotθ
Hence, LHS = RHS(Proved)
Question 16. Prove that cosθ(tanθ + 2)(2tanθ + 1) = 2secθ + 5sinθ
Solution:
We have
cosθ(tanθ + 2)(2tanθ + 1) = 2secθ + 5sinθ
Taking LHS
= cosθ(tanθ + 2)(2tanθ + 1)
= 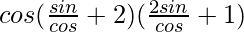
= 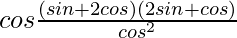
= 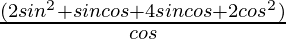
= 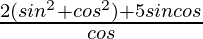
= 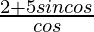
= 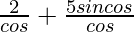
= 2secθ + 5sinθ
Hence, LHS = RHS(Proved)
Question 17. If x = 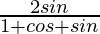 , prove that
, prove that 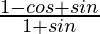 is also equal to x.
is also equal to x.
Solution:
We have
x = 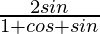
Taking LHS
= 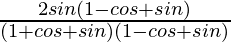
= 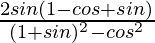
= 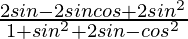
=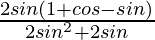
= 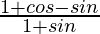
Question 18. If 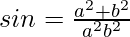 , then find the values of tanθ, secθ, and cosecθ
, then find the values of tanθ, secθ, and cosecθ
Solution:
We have
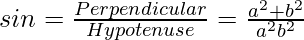
As we know that
cosθ = √1 – sin2θ -(1)
Now put the value of sinθ in eq(1)
cosθ = 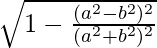
= 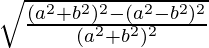
= 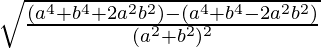
= 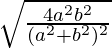
= 
So the value of cosθ = 
Now,
tanθ = 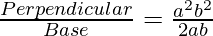
secθ = 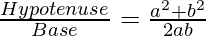
cosecθ = 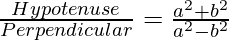
Alternative Method:
We have

We draw a △PQR right-angled at Q PR = a2 + b2 and PQ = a2 – b2

By Pythagoras theorem, we have
PR2 = PQ2 + QR2
QR2 = (a2 + b2)2 – (a2 – b2)2
QR2 = (a4 + b4 + 2a2b2) − (a4 + b4 − 2a2b2)
QR2 = 4a2b2
QR = 2ab
cosθ = 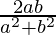
Now,
tanθ = 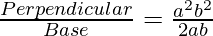
secθ = 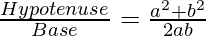
cosecθ = 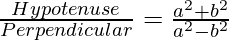
Question 19. If tanθ = a/b, then find the value of 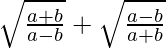
Solution:
We have
= 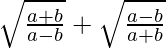
=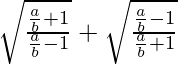
Now put tanθ = a/b
= 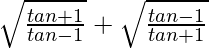
= 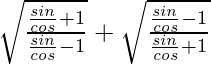
= 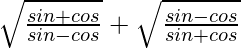
= 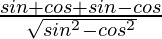
= 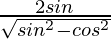
Question 20. If tanθ = a/b, show that 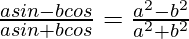 .
.
Solution:
We have
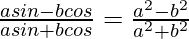
Taking LHS
=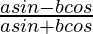
Dividing denominator and Numerator by cosθ
=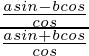
=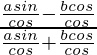
=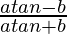
=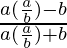
=
=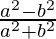
Hence, LHS = RHS(Proved)
Question 21. If cosecθ – sinθ = a3, secθ – cosθ = b3, then prove that a2b2(a2 + b2) = 1.
Solution:
Given: cosecθ – sinθ = a3
1/sinθ − sinθ = a3
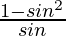 = a3
= a3
cos2θ/sinθ = a3
a = (cos2θ/sinθ)1/3
Similarly, b = (sin2θ/cosθ)1/3
Now putting the values of a and b in the following equation
Taking LHS
= a2b2(a2 + b2)
= a4b2 + a2b4
=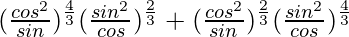
= cos6/3θ + sin6/3θ
= cos2θ + sin2θ
= 1
Hence, LHS = RHS (Proved)
Question 22. If cotθ(1 + sinθ) = 4m and cotθ(1 − sinθ) = 4n, prove that (m2 – n2)2 = mn.
Solution:
Given: cotθ(1 + sinθ) = 4m and cotθ(1 − sinθ) = 4n
Multiplying both the equations
16mn = cot2θ(1 – sin2θ)
16mn = 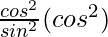
16mn = cos4θ/sin2θ
mn = cos4θ/16sin2θ -(1)
Now squaring the given equations
16m2 = cot2θ(1 + sinθ)2 and 16n2 = cot2θ(1 – sinθ)2
On subtracting both the equation, we get
16m2 – 16n2 = cot2θ(1 + sinθ)2 – cot2θ(1 – sinθ)2
16(m2 – n2) = cot2θ((1 + sinθ)2 – (1 – sinθ)2)
16(m2 – n2) = 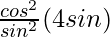
(m2 – n2) = cos2θ/4sinθ
On squaring both side, we get
(m2 – n2)2 = cos4θ/16sinθ -(2)
From equation(1) and (2)
(m2 – n2)2 = mn
Hence proved
Question 23. If sinθ + cosθ = m then prove that sin6θ + cos6θ = 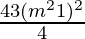 , where m2 ≤ 2.
, where m2 ≤ 2.
Solution:
Given: sinθ + cosθ = m
On squaring both side, we get
(sinθ + cosθ)2 = m2
= sin2θ + cos2θ + 2sinθcosθ = m2
= 2sinθcosθ = m2 − 1
Now,
Taking LHS
= sin6θ + cos6θ
Using a3 + b3 = (a + b)(a2 + b2 − ab)
= (sin2θ)3 + (cos2θ)3
= (sin2θ + cos2θ)(sin4θ + cos4θ − sin2θcos2θ)
= (1)((sin2θ)2 + (cos2θ)2 − sin2θcos2θ)
= (sin2θ + cos2θ)2 − 2sin2θcos2θ − sin2θcos2θ
= (1 − 3sin2θcos2θ)
= 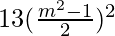
= 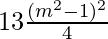
= 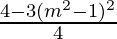
Hence, Proved.
Question 24. If a = secθ – tanθ and b = cosecθ + cotθ, then show that ab + a – b + 1 = 0.
Solution:
We have
a = secθ – tanθ and b = cosecθ + cotθ
and we have to proof that
ab + a – b + 1 = 0
So, taking LHS
ab + a – b + 1
Now put the values of a and b, we get
= (secθ – tanθ)(cosecθ + cotθ) – (secθ – tanθ) + (cosecθ + cotθ) + 1
= (1/cosθ – sinθ/cosθ)(1/sinθ + cosθ/sinθ) – (1/cosθ – sinθ/cosθ) + (1/sinθ + cosθ/sinθ) + 1
= 1/cosθsinθ + 1/cosθ x cosθ/sinθ – sinθ/cosθ x 1/sinθ – (sinθ/cosθ) x (cosθ/sinθ) + 1/cosθ – sinθ/cosθ – 1/sinθ – cosθ/sinθ + 1
= 1/cosθsinθ + 1/sinθ – 1/cosθ – 1 + 1/cosθ – sinθ/cosθ – 1/sinθ – cosθ/sinθ + 1
= 1/cosθsinθ – sinθ/cosθ – cosθ/sinθ
= 1 – sin2θ – cos2θ/sinθcosθ
= 1 – (sin2θ + cos2θ)/sinθcosθ
= 1 – 1/sinθcosθ
= 0
Hence, LHS = RHS (Proved)
Question 25. 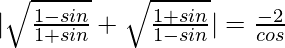 , where π/2 < θ < π.
, where π/2 < θ < π.
Solution:
We have

Taking LHS
= 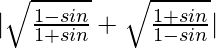
= 
= 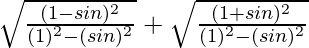
= 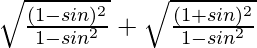
= 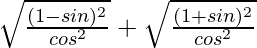
= 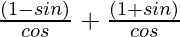
= 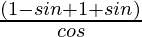
= 2/cosθ
Since π/2 < θ < π ,where cosθ is negative
So, -2/cosθ
Hence, LHS = RHS (Proved)
Question 26 (i). If Tn = sinnθ + cosnθ, prove that
\frac{T_3-T_5}{T_1}=\frac{T_5-T_7}{T_5}
Solution:
LHS = 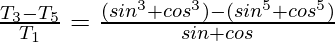
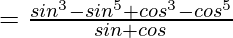

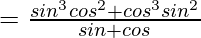
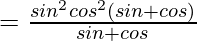
= sin2θcos2θ
RHS = 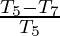
=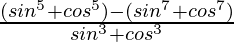
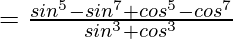

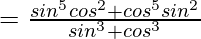
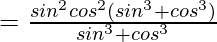
= sin2θcos2θ
Question 26 (ii). If Tn = sinnθ + cosnθ, prove that
2T6 – 3T4 + 1 = 0
Solution:
LHS = 2(sin6θ + cos6θ) – 3(sin4θ + cos4θ) + 1
Using (a3 + b3) = (a + b)(a2 + b2 – ab)
= 2(sin2θ + cos2θ)(sin4θ + cos4θ – sin2θcos2θ) – 3(sin4θ + cos4θ) + 1
= 2(1)(sin4θ + cos4θ – sin2θcos2θ) – 3(sin4θ + cos4θ) + 1
= 2sin4θ + 2cos4θ – 2sin2θcos2θ – 3sin4θ – 3cos4θ + 1
= -sin4θ – cos4θ – 2sin2θcos2θ + 1
= -(sin2θ + cos2θ)2 + 1
= -1 + 1 = 0 = RHS (Hence Proved)
Question 26 (iii). If Tn = sinnθ + cosnθ, prove that
6T10 – 15T8 + 10T6 – 1 = 0
Solution:
T6 = sin6θ + cos6θ
Using a3 + b3 = (a + b)(a2 + b2 − ab)
= (sin2x)3 + (cos2x)3
= (sin2x + cos2x)(sin4x + cos4x − sin2xcos2x)
Using a2 + b2 = (a + b)2 − 2ab
= (1)(sin4x + cos4x − sin2xcos2x)
= (sin2x)2 + (cos2x)2 − sin2xcos2x
= (sin2x + cos2x)2 − 3sin2xcos2
= 1 − 3sin2xcos2x
Similarly, we get the values of T8 & T10
T8 = (sin6x + cos6x)(sin2x + cos2x) − sin2xcos2x(sin4x + cos4x)
= 1 − 3sin2xcos2x − sin2xcos2x(1 − 2sin2xcos2x)
= 1 − 4sin2xcos2x + 2sin4xcos4x
T10 = sin10θ + cos10θ
= (sin6θ + cos6θ)(sin4θ + cos4θ) − sin4θcos4θ(sin2θ + cos2θ)
= (1 − 3sin2xcos2x)(1 − 2sin2xcos2x) − sin4xcos4x
= 1 − 5sin2xcos2x + 5sin4xcos4x
On putting the values of T6, T8 and T10 in the following equation
6T10 – 15T8 + 10T6 – 1
We get the value 0.
Hence Proved
Share your thoughts in the comments
Please Login to comment...