Class 11 RD Sharma Solutions – Chapter 13 Complex Numbers – Exercise 13.3
Last Updated :
21 Feb, 2021
Question 1. Find the square root of the following complex numbers.
(i) – 5 + 12i
(ii) -7 – 24i
(iii) 1 – i
(iv) – 8 – 6i
(v) 8 – 15i
(vi) 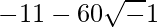
(vii) 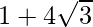
(viii) 4i
(ix) -i
Solution:
If b > 0, ![Rendered by QuickLaTeX.com \sqrt{a+ib}=\pm\left[\left(\frac{a+\sqrt{a^2+b^2}}{2}\right)^{\frac{1}{2}}+i\left(\frac{-a+\sqrt{a^2+b^2}}{2}\right)^{\frac{1}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-62b69331f0dfb4b958dfe4c45f2b5134_l3.png)
If b < 0, ![Rendered by QuickLaTeX.com \sqrt{a+ib}=\pm\left[\left(\frac{a+\sqrt{a^2+b^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-a+\sqrt{a^2+b^2}}{2}\right)^{\frac{1}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c1560bee11e70aa9b9555382da36939f_l3.png)
(i) – 5 + 12i
Given:
– 5 + 12i
We know, Z = a + ib
So, 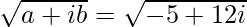
Here, b > 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{-5+12i}=\pm\left[\left(\frac{-5+\sqrt{(-5)^2+12^2}}{2}\right)^{\frac{1}{2}}+i\left(\frac{5+\sqrt{(-5)^2+12^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b>0]\\ =\pm\left[\left(\frac{-5+\sqrt{25+144}}{2}\right)^{\frac{1}{2}}+i\left(\frac{5+\sqrt{25+144}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-5+\sqrt{169}}{2}\right)^{\frac{1}{2}}+i\left(\frac{5+\sqrt{169}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-5+13}{2}\right)^{\frac{1}{2}}+i\left(\frac{5+13}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{8}{2}\right)^{\frac{1}{2}}+i\left(\frac{18}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[4^{\frac{1}{2}}+i9^{\frac{1}{2}}\right]\\ =\pm[2+3i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-733a1fc9776eaaf5799422101c38b884_l3.png)
∴ Square root of (– 5 + 12i) is ±[2 + 3i]
(ii) -7 – 24i
Given:
-7 – 24i
We know, Z = -7 – 24i
So, 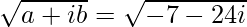
Here, b < 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{-7-24i}=\pm\left[\left(\frac{-7+\sqrt{(-7)^2+(-24)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{7+\sqrt{(-7)^2+(-24)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{-7+\sqrt{49+576}}{2}\right)^{\frac{1}{2}}-i\left(\frac{7+\sqrt{49+576}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-7+\sqrt{625}}{2}\right)^{\frac{1}{2}}-i\left(\frac{7+\sqrt{625}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-7+25}{2}\right)^{\frac{1}{2}}-i\left(\frac{7+25}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{18}{2}\right)^{\frac{1}{2}}-i\left(\frac{32}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[9^{\frac{1}{2}}-i16^{\frac{1}{2}}\right]\\ =\pm[3-4i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a20a25850a2b47665bf5d80c51b81d9_l3.png)
∴ Square root of (-7 – 24i) is ± [3 – 4i]
(iii) 1 – i
Given:
1 – i
We know, Z = (1 – i)
So, 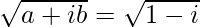
Here, b < 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{1-i}=\pm\left[\left(\frac{1+\sqrt{(1)^2+(-1)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-1+\sqrt{(1)^2+(-1)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{1+\sqrt{1+1}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-1+\sqrt{1+1}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{1+\sqrt{2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-1+\sqrt{2}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\sqrt{\frac{\sqrt2+1}{2}}\right)-i\left(\sqrt{\frac{\sqrt2-1}{2}}\right)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6b56f6ff6e111d3a4bbec4ccf98b8596_l3.png)
∴ Square root of (1 – i) is ± ![Rendered by QuickLaTeX.com \pm\left[\left(\sqrt{\frac{\sqrt2+1}{2}}\right)-i\left(\sqrt{\frac{\sqrt2-1}{2}}\right)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9ce6d301b4412e1e8529793e869c4000_l3.png)
(iv) -8 -6i
Given:
-8 -6i
We know, Z = -8 -6i
So, 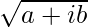 = -8 -6i
= -8 -6i
Here, b < 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{-8-6i}=\pm\left[\left(\frac{-8+\sqrt{(-8)^2+(-6)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{8+\sqrt{(-8)^2+(-6)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{-8+\sqrt{64+36}}{2}\right)^{\frac{1}{2}}-i\left(\frac{8+\sqrt{64+36}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-8+\sqrt{100}}{2}\right)^{\frac{1}{2}}-i\left(\frac{8+\sqrt{100}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-8+10}{2}\right)^{\frac{1}{2}}-i\left(\frac{8+10}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{2}{2}\right)^{\frac{1}{2}}-i\left(\frac{10}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[1^{\frac{1}{2}}-i9^{\frac{1}{2}}\right]\\ =\pm[1-3i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-058683232443b4679b1b6971684ee108_l3.png)
∴ Square root of (-8 -6i) is ± [1 – 3i]
(v) 8 – 15i
Given:
8 – 15i
We know, Z = 8 – 15i
So, 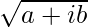 = 8 – 15i
= 8 – 15i
Here, b < 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{8-15i}=\pm\left[\left(\frac{8+\sqrt{(8)^2+(-15)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-8+\sqrt{(8)^2+(-15)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{8+\sqrt{64+225}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-8+\sqrt{64+225}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{8+\sqrt{289}}{2}\right)^{\frac{1}{2}}-i\left(\frac{-8+\sqrt{289}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{8+17}{2}\right)^{\frac{1}{2}}-i\left(\frac{-8+17}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{25}{2}\right)^{\frac{1}{2}}-i\left(\frac{9}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\frac{5}{\sqrt2}-\frac{13}{\sqrt2}\right]\\ =\pm\frac{1}{\sqrt2}(5-3i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b33ae047c6c1833328d76ef87f5d5aae_l3.png)
∴ Square root of (8 – 15i) is ± 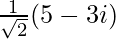
(vi) 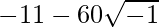
Given:
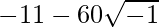
We know, Z = 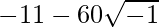
So, 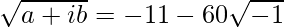
= -11 – 60i
Here, b < 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{-11-60i}=\pm\left[\left(\frac{-11+\sqrt{(-11)^2+(-60)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{11+\sqrt{(-11)^2+(60)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{-11+\sqrt{121+3600}}{2}\right)^{\frac{1}{2}}-i\left(\frac{11+\sqrt{121+3600}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-11+\sqrt{3721}}{2}\right)^{\frac{1}{2}}-i\left(\frac{11+\sqrt{3721}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{-11+61}{2}\right)^{\frac{1}{2}}-i\left(\frac{11+61}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{50}{2}\right)^{\frac{1}{2}}-i\left(\frac{72}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[25^{\frac{1}{2}-i36^{\frac{1}{2}}}\right]\\ =\pm(5-6i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5dc0992649e3368b8782c206085f73ac_l3.png)
∴ Square root of (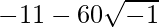 ) is ± (5 – 6i)
) is ± (5 – 6i)
(vii) 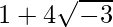
Given:
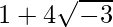
We know, Z = 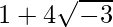
So, 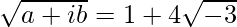
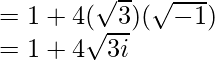
Here, b > 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{1+4\sqrt3i}=\pm\left[\left(\frac{1+\sqrt{(1)^2+(4\sqrt3)^2}}{2}\right)^{\frac{1}{2}}+i\left(\frac{-1+\sqrt{1^2+(4\sqrt3)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b>0]\\ =\pm\left[\left(\frac{1+\sqrt{1+48}}{2}\right)^{\frac{1}{2}}+i\left(\frac{-1+\sqrt{1+48}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{1+\sqrt{49}}{2}\right)^{\frac{1}{2}}+i\left(\frac{-1+\sqrt{49}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{1+7}{2}\right)^{\frac{1}{2}}+i\left(\frac{-1+7}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{8}{2}\right)^{\frac{1}{2}}+i\left(\frac{6}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[4^{\frac{1}{2}}+i3^{\frac{1}{2}}\right]\\ =\pm[2+\sqrt3i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-444f8b48b222cc6601d25e6aa06064ee_l3.png)
∴ Square root of 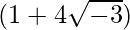 is ±
is ± 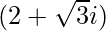
(viii) 4i
Given:
4i
We know, Z = 4i
So, 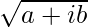 = 4i
= 4i
Here, b > 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{4i}=\pm\left[\left(\frac{0+\sqrt{(0)^2+(4)^2}}{2}\right)^{\frac{1}{2}}+i\left(\frac{0+\sqrt{0^2+(4)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b>0]\\ =\pm\left[\left(\frac{0+\sqrt{0+16}}{2}\right)^{\frac{1}{2}}+i\left(\frac{0+\sqrt{0+16}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{0+\sqrt{16}}{2}\right)^{\frac{1}{2}}+i\left(\frac{0+\sqrt{16}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{0+4}{2}\right)^{\frac{1}{2}}+i\left(\frac{0+4}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{4}{2}\right)^{\frac{1}{2}}+i\left(\frac{4}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[2^{\frac{1}{2}}+i2^{\frac{1}{2}}\right]\\ =\pm[\sqrt2+\sqrt2i]\\ =\pm\sqrt2(1+i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ca1fc56494ceb45f3ba31b84fb97ea7d_l3.png)
∴ Square root of 4i is ± 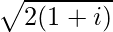
(ix) –i
Given:
-i
We know, Z = -i
So, 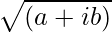 = -i
= -i
Here, b < 0
Let us simplify now,
![Rendered by QuickLaTeX.com \sqrt{-i}=\pm\left[\left(\frac{0+\sqrt{0^2+(-1)^2}}{2}\right)^{\frac{1}{2}}-i\left(\frac{0+\sqrt{0^2+(-1)^2}}{2}\right)^{\frac{1}{2}}\right]\ \ \ [Since\ b<0]\\ =\pm\left[\left(\frac{0+\sqrt{0+1}}{2}\right)^{\frac{1}{2}}-i\left(\frac{0+\sqrt{0+1}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{0+\sqrt{1}}{2}\right)^{\frac{1}{2}}-i\left(\frac{0+\sqrt{1}}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{0+1}{2}\right)^{\frac{1}{2}}-i\left(\frac{0+1}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\left(\frac{1}{2}\right)^{\frac{1}{2}}-i\left(\frac{1}{2}\right)^{\frac{1}{2}}\right]\\ =\pm\left[\frac{1}{\sqrt2}-\frac{i}{\sqrt2}\right]\\ =\pm\frac{1}{\sqrt2}(1-i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ececf7d8dda29280607c675f20c3109_l3.png)
∴ Square root of –i is ± 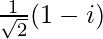
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...