Question 1. Calculate the mean deviation about the median of the following observation :
(i) 3011, 2780, 3020, 2354, 3541, 4150, 5000
(ii) 38, 70, 48, 34, 42, 55, 63, 46, 54, 44
(iii) 34, 66, 30, 38, 44, 50, 40, 60, 42, 51
(iv) 22, 24, 30, 27, 29, 31, 25, 28, 41, 42
(v) 38, 70, 48, 34, 63, 42, 55, 44, 53, 47
Solution:
(i) 3011, 2780, 3020, 2354, 3541, 4150, 5000
Calculating Median (M) of the following observation:
Arranging numbers in ascending order,
2354, 2780, 3011, 3020, 3541, 4150, 5000
Median is the middle number of all the observations.
Therefore, Median = 3020 and n = 7
| xi | |di| = |xi – 3020| |
| 3011 | 9 |
| 2780 | 240 |
| 3020 | 0 |
| 2354 | 666 |
| 3541 | 521 |
| 4150 | 1130 |
| 5000 | 1980 |
| Total | 4546 |
Calculating Mean Deviation:
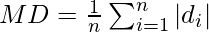
= 1/7 × 4546
= 649.42
Hence, Mean Deviation is 649.42.
(ii) 38, 70, 48, 34, 42, 55, 63, 46, 54, 44
Calculating Median (M) of the following observation:
Arranging numbers in ascending order,
34, 38, 42, 44, 46, 48, 54, 55, 63, 70
Median is the middle number of all the observations.
Here, the number of observations are even,
therefore the Median = (46 + 48)/2 = 47
Median = 47 and n = 10
| xi | |di| = |xi – 47| |
| 38 | 9 |
| 70 | 23 |
| 48 | 1 |
| 34 | 13 |
| 42 | 5 |
| 55 | 8 |
| 63 | 16 |
| 46 | 1 |
| 54 | 7 |
| 44 | 3 |
| Total | 86 |
Calculating Mean Deviation:
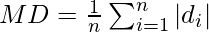
= 1/10 × 86
= 8.6
Hence, Mean Deviation is 8.6.
(iii) 34, 66, 30, 38, 44, 50, 40, 60, 42, 51
Calculating Median (M) of the following observation:
Arranging numbers in ascending order,
30, 34, 38, 40, 42, 44, 50, 51, 60, 66
Median is the middle number of all the observations.
Here, the number of observations are even,
therefore the Median = (42 + 44)/2 = 43
Median = 43 and n = 10
| xi | |di| = |xi – 43| |
| 30 | 13 |
| 34 | 9 |
| 38 | 5 |
| 40 | 3 |
| 42 | 1 |
| 44 | 1 |
| 50 | 7 |
| 51 | 8 |
| 60 | 17 |
| 66 | 23 |
| Total | 87 |
Calculating Mean Deviation:
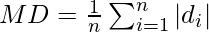
= 1/10 × 87
= 8.7
Hence, Mean Deviation is 8.7.
(iv) 22, 24, 30, 27, 29, 31, 25, 28, 41, 42
Calculating Median (M) of the following observation:
Arranging numbers in ascending order,
22, 24, 25, 27, 28, 29, 30, 31, 41, 42
Median is the middle number of all the observations.
Here, the number of observations are even,
therefore the Median = (28 + 29)/2 = 28.5
Median = 28.5 and n = 10
| xi | |di| = |xi – 28.5| |
| 22 | 6.5 |
| 24 | 4.5 |
| 30 | 1.5 |
| 27 | 1.5 |
| 29 | 0.5 |
| 31 | 2.5 |
| 25 | 3.5 |
| 28 | 0.5 |
| 41 | 12.5 |
| 42 | 13.5 |
| Total | 47 |
Calculating Mean Deviation:
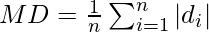
= 1/10 × 47
= 4.7
Hence, Mean Deviation is 4.7.
(v) 38, 70, 48, 34, 63, 42, 55, 44, 53, 47
Calculating Median (M) of the following observation:
Arranging numbers in ascending order,
34, 38, 43, 44, 47, 48, 53, 55, 63, 70
Median is the middle number of all the observation.
Here, the number of observations are even,
therefore the Median = (47 + 48)/2 = 47.5
Median = 47.5 and n = 10
| xi | |di| = |xi – 47.5| |
| 38 | 9.5 |
| 70 | 22.5 |
| 48 | 0.5 |
| 34 | 13.5 |
| 63 | 15.5 |
| 42 | 5.5 |
| 55 | 7.5 |
| 44 | 3.5 |
| 53 | 5.5 |
| 47 | 0.5 |
| Total | 84 |
Calculating Mean Deviation:
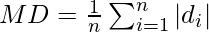
= 1/10 × 84
= 8.4
∴ The Mean Deviation is 8.4.
Question 2. Calculate the mean deviation from the mean for the following data :
(i) 4, 7, 8, 9, 10, 12, 13, 17
(ii) 13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17
(iii) 38, 70, 48, 40, 42, 55, 63, 46, 54, 44
(iv) 36, 72, 46, 42, 60, 45, 53, 46, 51, 49
(v) 57, 64, 43, 67, 49, 59, 44, 47, 61, 59
Solution:
(i) 4, 7, 8, 9, 10, 12, 13, 17
We know, Mean Deviation,
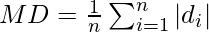
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
Now, x = [4 + 7 + 8 + 9 + 10 + 12 + 13 + 17]/8
= 80/8
= 10
Number of observations, n = 8
| xi | |di| = |xi – 10| |
| 4 | 6 |
| 7 | 3 |
| 8 | 2 |
| 9 | 1 |
| 10 | 0 |
| 12 | 2 |
| 13 | 3 |
| 17 | 7 |
| Total | 24 |
MD = 1/8 * 24
= 3
(ii) 13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17
Since,
Mean Deviation, 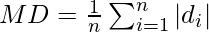
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
x = [13 + 17 + 16 + 14 + 11 + 13 + 10 + 16 + 11 + 18 + 12 + 17]/12
= 168/12
= 14
Number of observations, n = 12
| xi | |di| = |xi – 14| |
| 13 | 1 |
| 17 | 3 |
| 16 | 2 |
| 14 | 0 |
| 11 | 3 |
| 13 | 1 |
| 10 | 4 |
| 16 | 2 |
| 11 | 3 |
| 18 | 4 |
| 12 | 2 |
| 17 | 3 |
| Total | 28 |
Now,
MD = 1/12 × 28
= 2.33
(iii) 38, 70, 48, 40, 42, 55, 63, 46, 54, 44
We know that,
Mean Deviation, 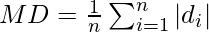
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
x = [38 + 70 + 48 + 40 + 42 + 55 + 63 + 46 + 54 + 44]/10
= 500/10
= 50
Number of observations, n = 10
| xi | |di| = |xi – 50| |
| 38 | 12 |
| 70 | 20 |
| 48 | 2 |
| 40 | 10 |
| 42 | 8 |
| 55 | 5 |
| 63 | 13 |
| 46 | 4 |
| 54 | 4 |
| 44 | 6 |
| Total | 84 |
MD = 1/10 × 84
= 8.4
(iv) 36, 72, 46, 42, 60, 45, 53, 46, 51, 49
Mean Deviation,
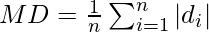
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
x = [36 + 72 + 46 + 42 + 60 + 45 + 53 + 46 + 51 + 49]/10
= 500/10
= 50
Number of observations, n = 10
| xi | |di| = |xi – 50| |
| 36 | 14 |
| 72 | 22 |
| 46 | 4 |
| 42 | 8 |
| 60 | 10 |
| 45 | 5 |
| 53 | 3 |
| 46 | 4 |
| 51 | 1 |
| 49 | 1 |
| Total | 72 |
MD = 1/10 × 72
= 7.2
(v) 57, 64, 43, 67, 49, 59, 44, 47, 61, 59
Mean Deviation,
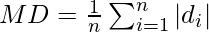
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
x = [57 + 64 + 43 + 67 + 49 + 59 + 44 + 47 + 61 + 59]/10
= 550/10
= 55
Number of observations, n = 10
| xi | |di| = |xi – 55| |
| 57 | 2 |
| 64 | 9 |
| 43 | 12 |
| 67 | 12 |
| 49 | 6 |
| 59 | 4 |
| 44 | 11 |
| 47 | 8 |
| 61 | 6 |
| 59 | 4 |
| Total | 74 |
MD = 1/10 × 74
= 7.4
Question 3. Calculate the mean deviation of the following income groups of five and seven members from their medians:
|
I
Income in ₹
|
II
Income in ₹
|
| 4000 | 3800 |
| 4200 | 4000 |
| 4400 | 4200 |
| 4600 | 4400 |
| 4800 | 4600 |
| | 4800 |
| | 5800 |
Solution:
Dataset I :
Since the data is arranged in ascending order,
4000, 4200, 4400, 4600, 4800
Median (Middle of ascending order observation) = 4400
Total observations, n = 5
Now, Mean Deviation,
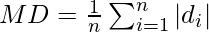
| xi | |di| = |xi – 4400| |
| 4000 | 400 |
| 4200 | 200 |
| 4400 | 0 |
| 4600 | 200 |
| 4800 | 400 |
| Total | 1200 |
MD(I) = 1/5 × 1200
= 240
Dataset II :
Since the data is arranged in ascending order,
3800, 4000, 4200, 4400, 4600, 4800, 5800
Median (Middle of ascending order observation) = 4400
Total observations, n = 7
Now, Mean Deviation,
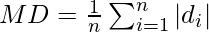
| xi | |di| = |xi – 4400| |
| 3800 | 600 |
| 4000 | 400 |
| 4200 | 200 |
| 4400 | 0 |
| 4600 | 200 |
| 4800 | 400 |
| 5800 | 1400 |
| Total | 3200 |
MD(II) = 1/7 × 3200
= 457.14
Therefore, the Mean Deviation of set 1, MD(I) is 240 and set 2, MD(II) is 457.14
Question 4. The lengths (in cm) of 10 rods in a shop are given below:
40.0, 52.3, 55.2, 72.9, 52.8, 79.0, 32.5, 15.2, 27.9, 30.2
(i) Find the mean deviation from the median.
(ii) Find the mean deviation from the mean also.
Solution:
(i) The mean deviation from the median
Arranging the data in ascending order,
15.2, 27.9, 30.2, 32.5, 40.0, 52.3, 52.8, 55.2, 72.9, 79.0
We know that,
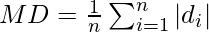
Since, the number of observations are even,
therefore Median = (40 + 52.3)/2 = 46.15
Median = 46.15
Also, number of observations, n = 10
| xi | |di| = |xi – 46.15| |
| 40.0 | 6.15 |
| 52.3 | 6.15 |
| 55.2 | 9.05 |
| 72.9 | 26.75 |
| 52.8 | 6.65 |
| 79.0 | 32.85 |
| 32.5 | 13.65 |
| 15.2 | 30.95 |
| 27.9 | 19.25 |
| 30.2 | 15.95 |
| Total | 167.4 |
MD = 1/10 * 167.4
=16.74
(ii) Mean deviation from the mean also.
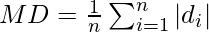
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
Now, x = [40.0 + 52.3 + 55.2 + 72.9 + 52.8 + 79.0 + 32.5 + 15.2 + 27.9 + 30.2]/10
= 458/10
= 45.8
And, number of observations, n = 10
| xi | |di| = |xi – 45.8| |
| 40.0 | 5.8 |
| 52.3 | 6.5 |
| 55.2 | 9.4 |
| 72.9 | 27.1 |
| 52.8 | 7 |
| 79.0 | 33.2 |
| 32.5 | 13.3 |
| 15.2 | 30.6 |
| 27.9 | 17.9 |
| 30.2 | 15.6 |
| Total | 166.4 |
MD = 1/10 * 166.4
= 16.64
Question 5. In question 1(iii), (iv), (v) find the number of observations lying between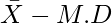 and
and  , where M.D. is the mean deviation from the mean.
, where M.D. is the mean deviation from the mean.
Solution:
(iii) 34, 66, 30, 38, 44, 50, 40, 60, 42, 51
We know that,
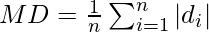
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
x = [34 + 66 + 30 + 38 + 44 + 50 + 40 + 60 + 42 + 51]/10
= 455/10
= 45.5
And, number of observations, n = 10
| xi | |di| = |xi – 45.5| |
| 34 | 11.5 |
| 66 | 20.5 |
| 30 | 15.5 |
| 38 | 7.5 |
| 44 | 1.5 |
| 50 | 4.5 |
| 40 | 5.5 |
| 60 | 14.5 |
| 42 | 3.5 |
| 51 | 5.5 |
| Total | 90 |
MD = 1/10 × 90
= 9
Now,
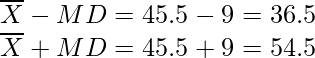
So, There are total 6 observation between 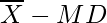 and
and 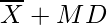
(iv) 22, 24, 30, 27, 29, 31, 25, 28, 41, 42
We know that,
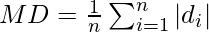
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
x = [22 + 24 + 30 + 27 + 29 + 31 + 25 + 28 + 41 + 42]/10
= 299/10
= 29.9
Also, number of observations, n = 10
| xi | |di| = |xi – 29.9| |
| 22 | 7.9 |
| 24 | 5.9 |
| 30 | 0.1 |
| 27 | 2.9 |
| 29 | 0.9 |
| 31 | 1.1 |
| 25 | 4.9 |
| 28 | 1.9 |
| 41 | 11.1 |
| 42 | 12.1 |
| Total | 48.8 |
MD = 1/10 × 48.8
= 4.88
And,
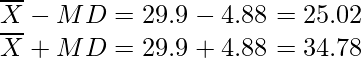
So, there are 5 observations in between.
(v) 38, 70, 48, 34, 63, 42, 55, 44, 53, 47
We know that,
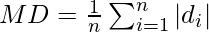
Where, |di| = |xi – x|
So, let us assume x to be the mean of the given observation.
x = [38 + 70 + 48 + 34 + 63 + 42 + 55 + 44 + 53 + 47]/10
= 494/10
= 49.4
Number of observations, n = 10
| xi | |di| = |xi – 49.4| |
| 38 | 11.4 |
| 70 | 20.6 |
| 48 | 1.4 |
| 34 | 15.4 |
| 63 | 13.6 |
| 42 | 7.4 |
| 55 | 5.6 |
| 44 | 5.4 |
| 53 | 3.6 |
| 47 | 2.4 |
| Total | 86.8 |
MD = = 1/10 × 86.8
= 8.68
Also,
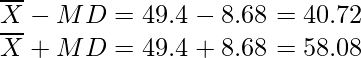
There are 6 observations in between.
Question 6. Show that the two formulae for the standard deviation of the ungrouped data 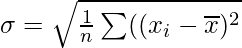 and
and 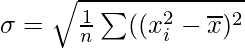 are equivalent, where
are equivalent, where 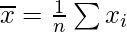
Solution:
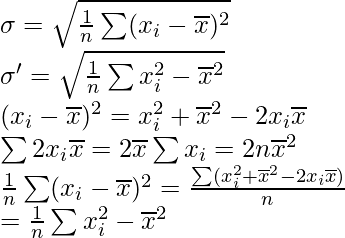
Share your thoughts in the comments
Please Login to comment...