Class 10 RD Sharma Solutions – Chapter 7 Statistics – Exercise 7.2
Last Updated :
21 Dec, 2020
Question1: The number of telephone calls received at an exchange per interval for 250 successive one-minute intervals are given in the following frequency table:
Number of calls 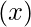
| 0
| 1
| 2
| 3
| 4
| 5
| 6
|
Number of intervals 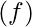
| 15
| 24
| 29
| 46
| 54
| 43
| 39
|
Compute the mean number of calls per interval.
Solution:
Let the assumed mean(A) be =3 (Generally we choose the middle element to be the assumed mean, but it’s not mandatory),
hence, the table is,
Number of calls 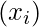 | Number of intervals 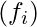
| 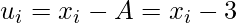
| 
|
0
| 15
| -3
| -45
|
1
| 24
| -2
| -48
|
2
| 29
| -1
| -29
|
3
| 46
| 0
| 0
|
4
| 54
| 1
| 54
|
5
| 43
| 2
| 86
|
6
| 39
| 3
| 117
|
| | 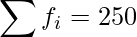
|
| 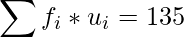
|
hence, mean of the calls = 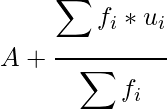
= 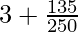
= 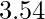
Therefore, mean number of calls per interval is 3.54
Question 2: Five coins were simultaneously tossed 1000 times, and at each toss the number of heads was observed. The number of tosses during which 0, 1, 2, 3, 4, and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.
Number of heads per toss 
| 0
| 1
| 2
| 3
| 4
| 5
|
Number of tosses 
| 38
| 144
| 342
| 287
| 164
| 25
|
Solution:
Let the assumed mean (A) be = 2
hence, the table is,
Number of heads per toss 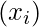
| Number of tosses 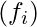
| 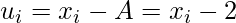
| 
|
0
| 38
| -2
| -76
|
1
| 144
| -1
| -144
|
2
| 342
| 0
| 0
|
3
| 287
| 1
| 287
|
4
| 164
| 2
| 328
|
5
| 25
| 3
| 75
|
| 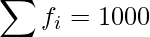
|
| 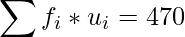
|
Mean number of head per toss = 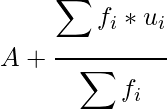
= 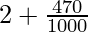
= 2.47
Therefore, mean number of head per toss is 2.47
Question 3: The following table gives the number of branches and number of plants in the garden of a school.
Number of branches 
| 2
| 3
| 4
| 5
| 6
|
Number of plants 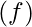
| 49
| 43
| 57
| 38
| 13
|
Calculate the average number of branches per plant.
Solution:
Let the assumed mean(A) be = 4
hence, the table is,
Number of branches 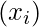
| Number of plants 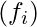
| 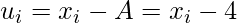
| 
|
2
| 49
| -2
| -98
|
3
| 43
| -1
| -43
|
4
| 57
| 0
| 0
|
5
| 38
| 1
| 38
|
6
| 13
| 2
| 26
|
| 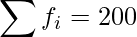
|
| 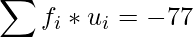
|
Average Number of branches per plant = 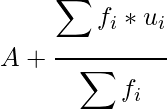
= 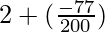
= 3.615
Therefore, mean number of branches per plant is 3.615
Question 4: The following table gives the number of children of 150 families in a village
Number of children 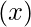
| 0
| 1
| 2
| 3
| 4
| 5
|
Number of families 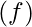
| 10
| 21
| 55
| 42
| 15
| 7
|
Find the average number of children per family.
Solution:
Let the assumed mean(A) be = 2
Hence, the table is,
Number of children 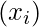
| Number of families 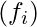
| 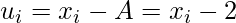
| 
|
0
| 10
| -2
| -20
|
1
| 21
| -1
| -21
|
2
| 55
| 0
| 0
|
3
| 42
| 1
| 42
|
4
| 15
| 2
| 30
|
5
| 7
| 3
| 21
|
| 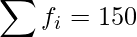
|
| 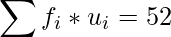
|
Average number of children per family = 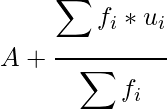
= 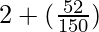
= 2.35 (approximately)
Therefore, the average number of children per family is 2.35 (approximately)
Question 5: The marks obtained out of 50, by 102 students in a Physics test are given in the frequency table below:
Marks 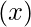
| 15
| 20
| 22
| 24
| 25
| 30
| 33
| 38
| 45
|
Frequency 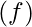
| 5
| 8
| 11
| 20
| 23
| 18
| 13
| 3
| 1
|
Find the average number of marks.
Solution:
Let the assume mean (A) be = 25
hence, the table is,
Marks 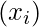
| Frequency 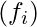
| 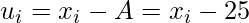
| 
|
15
| 5
| -10
| -50
|
20
| 8
| -5
| -40
|
22
| 11
| -3
| -33
|
24
| 20
| -1
| -20
|
25
| 23
| 0
| 0
|
30
| 18
| 5
| 90
|
33
| 13
| 8
| 104
|
38
| 3
| 13
| 39
|
45
| 1
| 20
| 20
|
| 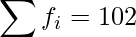
|
| 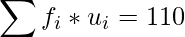
|
Average number of marks = 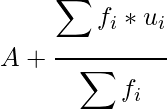
= 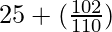
= 26.08 (approximately)
Therefore, average number of marks is 26.08 (approximately)
Question 6: The number of students absent in a class was recorded every day for 120 days and the information is given in the following
Number of students absent 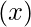
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
|
Number of Days 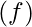
| 1
| 4
| 10
| 50
| 34
| 15
| 4
| 2
|
Find the mean number of students absent per day.
Solution:
Let mean assumed mean (A) be = 3
Number of students absent 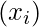
| Number of Days 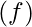
| 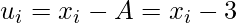
| 
|
0
| 1
| -3
| -3
|
1
| 4
| -2
| -8
|
2
| 10
| -1
| -10
|
3
| 50
| 0
| 0
|
4
| 34
| 1
| 34
|
5
| 15
| 2
| 30
|
6
| 4
| 3
| 12
|
7
| 2
| 4
| 8
|
| 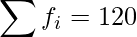
|
| 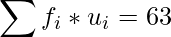
|
Mean number of students absent per day = 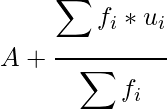
= 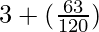
= 3.525
Therefore, the mean number of students absent per day is 3.525
Question 7: In the first proof of reading of a book containing 300 pages the following distribution of misprints was obtained:
Number of misprints per page 
| 0
| 1
| 2
| 3
| 4
| 5
|
Number of page 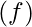
| 154
| 95
| 36
| 9
| 5
| 1
|
Find the average number of misprints per page.
Solution:
Let the assumed mean (A) be = 2
Number of misprints per page 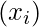
| Number of page 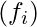
| 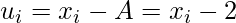
| 
|
0
| 154
| -2
| -308
|
1
| 95
| -1
| -95
|
2
| 36
| 0
| 0
|
3
| 9
| 1
| 9
|
4
| 5
| 2
| 10
|
5
| 1
| 3
| 3
|
| 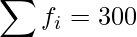
|
| 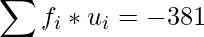
|
Average number of misprints per day = 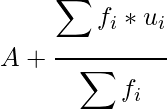
= 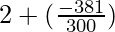
= 0.73
Therefore, the average number of misprints per day is 0.73
Question 8: Find the mean from the following frequency distribution of marks at a test in statistics:
Number of accidents 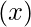
| 0
| 1
| 2
| 3
| 4
|
Number of workers 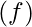
| 70
| 52
| 34
| 3
| 1
|
Find the average number of misprints per page.
Solution:
Let the assumed mean (A) = 2
Number of accidents 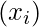
| Number of workers 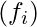
| 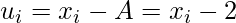
| 
|
0
| 70
| -2
| -140
|
1
| 52
| -1
| -52
|
2
| 34
| 0
| 0
|
3
| 3
| 1
| 3
|
4
| 1
| 2
| 2
|
| 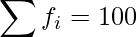
|
| 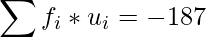
|
Average no of accidents per day workers = 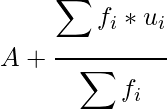
= 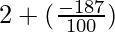
= 0.83
Therefore, average no of accidents per day workers 0.83
Question 9: Find the mean from the following frequency distribution of marks at a test in statistics:
Marks 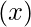
| 5
| 10
| 15
| 20
| 25
| 30
| 35
| 40
| 45
| 50
|
Number of students 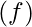
| 15
| 50
| 80
| 76
| 72
| 45
| 39
| 9
| 8
| 6
|
Solution:
Let the assumed mean (A) be = 25
Marks 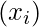
| Number of students 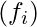
| 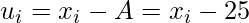
| 
|
5
| 15
| -20
| -300
|
10
| 50
| -15
| -750
|
15
| 80
| -10
| -800
|
20
| 76
| -5
| -380
|
25
| 72
| 0
| 0
|
30
| 45
| 5
| 225
|
35
| 39
| 10
| 390
|
40
| 9
| 15
| 135
|
45
| 8
| 20
| 160
|
50
| 6
| 25
| 150
|
| 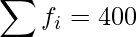
|
| 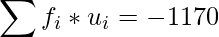
|
Mean = 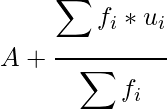
= 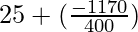
= 22.075
Therefore, the mean is 22.075
Share your thoughts in the comments
Please Login to comment...