Class 11 RD Sharma Solutions – Chapter 13 Complex Numbers – Exercise 13.2 | Set 2
Last Updated :
30 Apr, 2021
Question 14. If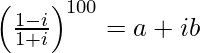 , find (a, b).
, find (a, b).
Solution:
We have,
=>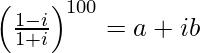
=>![Rendered by QuickLaTeX.com \left[\frac{(1-i)^2}{(1+i)(1-i)}\right]^{100}=a+ib](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-76713589ac91a3642b5b99d3a3ccd3ee_l3.png)
=>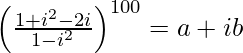
=>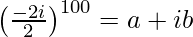
=> (−i)100 = a + ib
=> a + ib = 1
On comparing real and imaginary parts on both sides, we get,
=> (a, b) = (1, 0)
Question 15. If a = cos θ + i sin θ, find the value of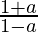 .
.
Solution:
Given a = cos θ + i sin θ, we get,
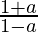 =
=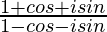
=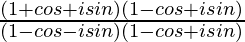
=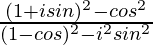
=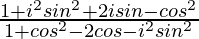
=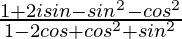
=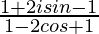
=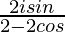
=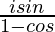
=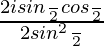
=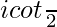
Therefore, the value of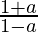 is
is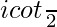 .
.
Question 16. Evaluate the following :
(i) 2x3 + 2x2 − 7x + 72, when x = (3−5i)/2
Solution:
We have, x = (3−5i)/2
=> 2x = 3 − 5i
=> 2x − 3 = −5i
=> (2x − 3)2 = 25i2
=> 4x2 + 9 − 12x = −25
=> 4x2 − 12x + 34 = 0
=> 2x2 − 6x + 17 = 0
Now, 2x3 + 2x2 − 7x + 72 = x (2x2 − 6x + 17) + 6x2 − 17x + 2x2 − 7x + 72
= x (0) + 8x2 − 24x + 72
= 4 (2x2 − 6x + 17) + 4
= 4 (0) + 4
= 4
Therefore, the value of 2x3 + 2x2 − 7x + 72 is 4.
(ii) x4 − 4x3 + 4x2 +8x +44, when x = 3 + 2i
Solution:
We have, x = 3 + 2i
=> x − 3 = 2i
=> (x − 3)2 = (2i)2
=> x2 + 9 − 6x = 4i2
=> x2 − 6x + 9 + 4 = 0
=> x2 − 6x + 13 = 0
Now, x4 − 4x3 + 4x2 + 8x + 44 = x2 (x2 − 6x + 13) + 6x3 − 13x2 − 4x3 + 4x2 + 8x + 44
= 2x3 − 9x2 + 8x + 44
= 2x (x2 − 6x + 13) + 12x2 − 26x − 9x2 + 8x + 44
= 3x2 − 18x + 44
= 3 (x2 − 6x + 13) + 5
= 5
Therefore, the value of x4 − 4x3 + 4x2 + 8x + 44 is 5.
(iii) x4 + 4x3 + 6x2 + 4x + 9, when x = −1 + i√2
Solution:
We have, x = −1 + i√2
=> x + 1 = i√2
=> (x + 1)2 = 2i2
=> x2 + 1 + 2x = −2
=> x2 + 2x + 3 = 0
Now, x4 + 4x3 + 6x2 + 4x + 9 = x2 (x2 + 2x + 3) − 2x3 − 3x2 + 4x3 + 6x2 + 4x + 9
= 2x3 + 3x2 + 4x + 9
= 2x (x2 + 2x + 3) − 4x2 − 6x + 3x2 + 4x + 9
= − x2 − 2x + 9
= − (x2 + 2x + 3) + 3 + 9
= 3 + 9
= 12
Therefore, the value of x4 + 4x3 + 6x2 + 4x + 9 is 12.
(iv) x6 + x4 + x2 + 1, when x = (1+i)/√2
Solution:
We have, x = (1+i)/√2
=> √2x = 1 + i
=> 2x2 = 1 + i2 + 2i
=> 2x2 = 2i
=> 4x4 = 4i2
=> x4 = −1
=> x4 + 1 = 0
Now, x6 + x4 + x2 + 1 = (x6 + x2) + (x4 +1)
= x6 + x2
= x2 (x4 + 1)
= 0
Therefore, the value of x6 + x4 + x2 + 1 is 0.
(v) 2x4 + 5x3 + 7x2 − x + 41, when x = −2 − √3i
Solution:
We have, x = −2 − √3i
x2 = (−2 − √3i)2 = 4 + 4√3i + 3i2 = 1 + 4√3i
x3 = (1 + 4√3i) (−2 − √3i) = −2 − √3i − 8√3i −12i2 = 10 − 9√3i
x4 = (1 + 4√3i)2 = 1 + 8√3i + 48i2 = −47 + 8√3i
Now, 2x4 + 5x3 + 7x2 − x + 41 becomes,
= 2(−47 + 8√3i) + 5(10 − 9√3i) + 7(1 + 4√3i) − (−2 − √3i) + 41
= −94 + 16√3i + 50 − 45√3i + 7 + 28√3i + 2 + √3i + 41
= 6
Therefore, the value of 2x4 + 5x3 + 7x2 − x + 41 is 6.
Question 17. For a positive integer n, find the value of (1−i)n (1−1/i)n.
Solution:
We have,
(1−i)n (1−1/i)n = (1−i)n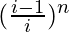
=![Rendered by QuickLaTeX.com \left[\frac{(1-i)^2}{-i}\right]^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c0be684058959bb956147d2230f29128_l3.png)
=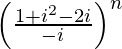
=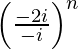
= 2n
Therefore, the value of (1−i)n (1−1/i)n is 2n.
Question 18. If (1+i)z = (1−i)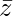 , then show that z = −i
, then show that z = −i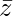 .
.
Solution:
We have,
=> (1+i)z = (1−i)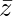
=> z =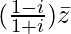
=> z =![Rendered by QuickLaTeX.com \left[\frac{(1-i)^2}{(1+i)(1-i)}\right]\bar{z}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f25cd1f544136f76788eea9cb5957ed2_l3.png)
=> z =![Rendered by QuickLaTeX.com \left[\frac{1+i^2-2i}{1-i^2}\right]\bar{z}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-102d383b184249dab3786f178ce66e20_l3.png)
=> z =![Rendered by QuickLaTeX.com \left[\frac{-2i}{2}\right]\bar{z}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff74a2056f160cc36330275ea8b1c4a_l3.png)
=> z = −i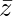
Hence proved.
Question 19. Solve the system of equations: Re(z2) = 0, |z| = 2.
Solution:
Let z = x + iy.
Now z2 = (x + iy)2
= x2 + i2y2 + 2xyi
= x2 − y2 + 2xyi
We have, Re(z2) = 0
=> x2 − y2 = 0 . . . . (1)
Also, it is given, |z| = 2.
=>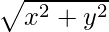 = 2
= 2
=> x2 + y2 = 4 . . . . (2)
Solving (1) and (2), we get, x = ±√2 and y = ±√2.
Therefore, x + iy = ±√2 ± √2i .
Question 20. If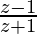 is purely imaginary number (z≠−1), find the value of |z|.
is purely imaginary number (z≠−1), find the value of |z|.
Solution:
Let z = x + iy
We have,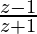
=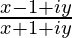
=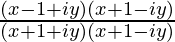
=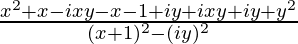
=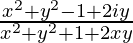
=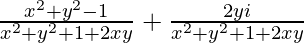
As the complex number is purely imaginary, therefore,
=> Re(z) = 0
=>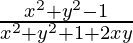 = 0
= 0
=> x2 + y2 = 1
=>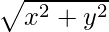 = 1
= 1
=> |z| = 1
Therefore, the value of |z| is 1.
Question 21. If z1 is a complex number other than −1 such that |z1| = 1 and z2 =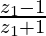 ,then show that the real parts of z2 is zero.
,then show that the real parts of z2 is zero.
Solution:
Given |z| = 1
=> |z|2 = 1
=> x2 + y2 = 1 . . . . (1)
Let z1 = x + iy and z2 = a + ib.
According to the question, we have,
=> z2 =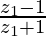
=> a + ib =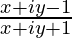
=> a + ib =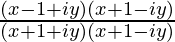
=> a + ib =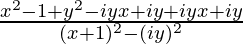
=> a + ib =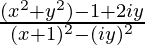
Using (1) we get,
=> a + ib =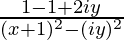
=> a + ib =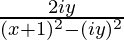
On comparing the real and imaginary parts on both sides, we get a = 0.
Therefore, the real parts of z2 is 0. Hence proved.
Question 22. If |z+1| = z + 2(1+i), find z.
Solution:
Let z = x + iy. According to the question, we have,
=> |x + iy + 1| = x + iy + 2(1 + i)
=>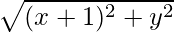 = (x + 2) + i(y + 2)
= (x + 2) + i(y + 2)
On comparing the real and imaginary parts, we get
=> y + 2 = 0
=> y = −2
And also,
=> x + 2 =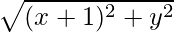
=> (x + 2)2 = (x+1)2 + y2
=> x2 + 4 + 4x = x2 + 2x + 1+ y2
=> 2x = y2 − 3
=> 2x = 4 − 3
=> 2x = 1
=> x = 1/2
Therefore, z = x + iy = 1/2 −2i.
Question 23. Solve the equation: |z| = z + 1 + 2i.
Solution:
Let z = x + iy. According to the question, we have,
=> |z| = z + 1 + 2i
=> |x + iy| = x + iy + 1 + 2i
=>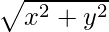 = (x + 1) + (y + 2)i
= (x + 1) + (y + 2)i
=> x2 + y2 = (x+1)2 + (y+2)2i2 + 2 (x+1) (y+2)i
=> x2 + y2 = x2+1 + 2x − y2 − 1 + 2y + 2 (x+1) (y+2)i
=> 2y2 − 2x + 4y + 4 = 2i (x+1) (y+2)
=> y2 − x + 2y + 2 = i (x+1) (y+2)
On comparing both sides, we get,
=> (x+1) (y+2) = 0
=> x = −1 and y = −2
Also, y2 − x + 2y + 2 = 0
Taking x = −1, we get y2 − (−1) + 2y + 2 = 0
=> y2 + 2y + 3 = 0, which doesn’t have a solution as the roots are imaginary.
Taking y = −2, (4 − x −4 + 2) = 0
=> x = 2
Therefore, z = x + iy = 2 − 2i.
Question 24. What is the smallest positive integer n for which (1+i)2n = (1−i)2n?
Solution:
We are given,
=> (1+i)2n = (1−i)2n
=>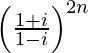 = 1
= 1
=>![Rendered by QuickLaTeX.com \left[\frac{(1+i)^2}{(1-i)(1+i)}\right]^{2n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c7f5a48cf16d51c8b8cfa55fde1f9e4_l3.png) = 1
= 1
=>![Rendered by QuickLaTeX.com \left[\frac{1+i^2+2i}{1-i^2}\right]^{2n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cadfc151efc249dd0fed27d3084a54dd_l3.png) = 1
= 1
=>![Rendered by QuickLaTeX.com \left[\frac{2i}{2}\right]^{2n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa515770ea5ca85f03ffa03fd137bd51_l3.png) = 1
= 1
=> i2n = 1
=> i2n = i4
=> 2n = 4
=> n = 2
Therefore, the smallest positive integer n for which (1+i)2n = (1−i)2n is 2.
Question 25. If z1, z2, z3 are complex numbers such that |z1| = |z2| = |z3| =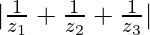 = 1, then find the value of |z1 + z2 + z3|.
= 1, then find the value of |z1 + z2 + z3|.
Solution:
We are given,
|z1| = |z2| = |z3| =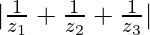 = 1
= 1
Now, |z1 + z2 + z3| =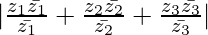
=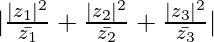
=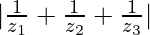
= 1
Therefore, the value of |z1 + z2 + z3| is 1.
Question 26. Find the number of solutions of z2 + |z|2 = 0.
Solution:
Let z = x + iy. We have,
=> z2 + |z|2 = 0
=> (x + iy)2 + |x + iy|2 = 0
=> x2 + i2y2 + 2xyi + x2 + y2 = 0
=> x2 − y2 + 2xyi + x2 + y2 = 0
=> 2x2 + 2xyi = 0
On comparing the real and imaginary parts on both sides, we get
=> 2x2 = 0 and 2xy = 0
=> x = 0 and y ∈ R
Therefore, z = 0 + iy, where y ∈ R.
Share your thoughts in the comments
Please Login to comment...