Class 11 RD Sharma Solutions – Chapter 20 Geometric Progressions- Exercise 20.5 | Set 2
Last Updated :
21 Feb, 2021
Question 12. If (a – b), (b – c), (c – a) are in G.P., then prove that (a + b + c)2 = 3(ab + bc + ca)
Solution:
Given: (a – b), (b – c), (c – a) are in G.P.
(b – c)2 = (a – b)(c – a)
b2 + c2 – 2bc = ac – a2 – bc + ab
b2 + c2 + a2 = ac + bc + ab -(1)
Now,
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
= ac + bc + ab + 2ab + 2bc + 2ca
So, using eq(1), we get
= 3ab + 3bc + 3ca
(a + b + c)2 = 3(ab + bc + ca)
LHS = RHS
Hence, proved
Question 13. If a, b, c are in G.P., then prove that:
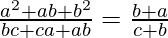
Solution:
Given: a, b, c are in G.P.
So, a, b = ar, c = ar2
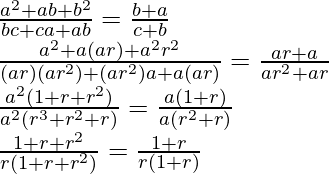
1/r = 1/r
L.H.S = R.H.S
Hence, proved 
Question 14. If the 4th, 10th, and 16th terms of a G.P. are x, y, and z respectively. Prove that x, y, z are in G.P.
Solution:
Let us considered the 4th term = ar3
10th term = ar9
16th term = ar15
So, ar9 = 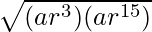 = ar9
= ar9
Therefore, 4th, 10th, 16th terms are also in G.P.
Hence, proved
Question 15. If a, b, c are in A.P. and a, b, d are in G.P., then prove that a, a – b, d – c are in G.P.
Solution:
Given: a, b, c are in A.P.
2b = a + c -(1)
also,
a, b, d are in G.P., so
b2 = ad -(2)
Now,
(a – b)2 = a2 + b2 – 2ab
= a2 + ad – a(a + c)
From eq(1) and (2), we get
= a2 + ad – a2 – ac
= ad – ac
(a – b)2 = a(d – c)
(a – b)/a = (d – c)/(a – b)
Hence, proved a, (a – b), (d – c) are in G.P.
Question 16. If pth, qth, rth and sth terms of an A.P. be in G.P., then prove that p – q, q – r, r – s are in G.P.
Solution:
Let us considered R be common ratio,
Given: ap, aq, ar, as of AP are in GP
R = ![Rendered by QuickLaTeX.com \frac{a_q}{a_p}=\frac{a_r}{a_q}\\ =\frac{a_q-a_r}{a_p-a_q}\ \ \ -(Using \ ratio\ property)\\ =\frac{[a+(q-1)d]-[a+(r-1)d]}{[a+(p-1)d]-[a+(q-1)d]}\\ =\frac{(q-r)d}{(p-q)d}\\ R=\frac{q-r}{p-q}\ \ \ \ -(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6830ce404e56bed6e979ad0f3d0b86a2_l3.png)
Now,
![Rendered by QuickLaTeX.com R=\frac{a_r}{a_q}=\frac{a_s}{a_r}\\ =\frac{a_r-a_s}{a_q-a_r}\ \ \ \ -(Using \ ratio\ property)\\ =\frac{[a+(r-1)d]-[a+(s-1)d]}{[a+(q-1)d]-[a+(r-1)d]}\\ =\frac{(r-s)d}{(q-r)d}\\ R=\frac{r-s}{q-r}\ \ \ \ \ -(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e3f796672177391a1b0f90c3254b315_l3.png)
Using eq(1) and (2), we get
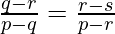
Hence, proved (p – q), (q – r), (r – s) are in G.P.
Question 17. If 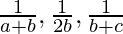 are the three consecutive terms of an A.P., prove that a, b, c are the three consecutive terms of a G.P.
are the three consecutive terms of an A.P., prove that a, b, c are the three consecutive terms of a G.P.
Solution:
Given: \frac{1}{a+b},\frac{1}{2b},\frac{1}{b+c} are in A.P.
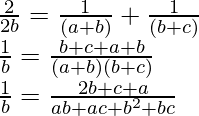
ab + ac + b2 + bc = 2b2 + bc + ba
b2 + ac = 2b2
b2 = ac
Hence, proved a, b , c are in G.P.
Question 18. If xa = xb/2 zb/2 = zc, then prove that 1/a, 1/b, 1/c are in A.P.
Solution:
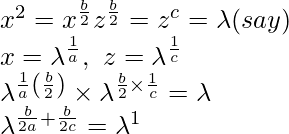
b/2a + b/2c = 1
1/a + 1/c = 2/b
Hence, 1/a, 1/b, 1/c are in A.P.
Question 19. If a, b, c are in A.P., b, c, d are in G.P. and 1/c, 1/d, 1/e are in A.P., prove that a, c, e are in G.P.
Solution:
Given: a, b, c are in A.P.
2b = a + c -(1)
Also, b, c, d are in G.P.
c2 = bd -(2)
1/c, 1/d, 1/e are in A.P.
2/d = 1/c + 1/e -(3)
We need to prove that
a, b, c are in G.P.
c2 = ae
Now,
![Rendered by QuickLaTeX.com c^2=bd=2b\times\frac{d}{2}\\ ⇒ c^2=(a+c)\times\frac{ce}{c+e}\\ ⇒ c^2=\frac{(a+c)ce}{c+e}\ \ \ \ \ \left[\because\frac{2}{d}=\frac{e+c}{ce}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2676f75793b569623f1846ef696c41f2_l3.png)
c2(c + e) = ace + c2e
c3 + c2e = ace + c2e
c3 = ace
c2 = ae
Hence, proved.
Question 20. If a, b, c are in A.P. and a, x, b and b, y, c are in G.P., show that x2, b2, y2 are in A.P.
Solution:
Given: a, b, c are in A.P.
2b = a + c -(1)
Also, a, x, b are in G.P.
x = ab -(2)
and b, y, c are in G.P.
y2 = bc -(3)
Now
2b2 = x2 + y2
= (ab) + (bc) -(By using eq(2) and (3))
2b2 = b(a + c)
2b2 = b(2b) -(By using eq(1))
2b2 = 2b2
L.H.S = R.H.S
2b2 = x2 + y2
Hence, x2, b2, y2 are in A.P.
Question 21. If a, b, c are in A.P. and a, b, d are in G.P., show that a, (a – b), (d – c) are in G.P.
Solution:
Given: a, b, c are in A.P.
2b = a + c -(1)
Also, a, b, d are in G.P.
b2 = ad -(2)
Now
(a – b)2 = a(d – c) -(By using eq(2))
a2 – 2ab = -ac
a2 – 2ab = ab – ac
a(a – b) = a(b – c)
a – b = a – c
2b = a + c
a + c = a + c, -(By using eq(1))
L.H.S = R.H.S
Hence, a, (a – b), (d – c) are in G.P.
Question 22. If a, b, c are three real numbers in G.P. and a + b + c = xb, then prove that either x < -1 or x > 3.
Solution:
Let us considered r be the common ratio of G.P.
So, a, b = ar, c = ar2
a + b + c = xb
a + ar + ar2 = x(ar)
a(1 + r + r2) = x(ar)
r2 + (1 – x)r + 1 = 0
Here, r is real, so
D ≥ 0
(1 – x)2 – 4(1)(1) ≥ 0
1 + x2 -2x – 4 ≥ 0
x2 – 2x – 3 ≥ 0
(x – 3)(x + 1) ≥ 0
Hence, x < -1 or x > 3
Question 23. If pth, qth and rth terms of a A.P. and G.P. are both a, b and c respectively, show that ab-c bc-a ca-b = 1.
Solution:
Let us considered the A.P. be A, A + D, A + 2D, …. and G.P. be x, xR, xR2,
Then
a = A + (p – 1)D, B = A + (q – 1)D, c = A + (r – 1)D
a – b = (p – q)D, b – c = (q – r)D, c – a = (r – p)D
Also a = XRp-1, b = xRq-1, c = xRr-1
Hence, ab-c.bc-a.ca-b = (xRp-1)(q-r)D.(xRq-1)(r-p)D.(xRr-1)(p-q)D
= x(q-r+r-p+p-q)D.R[(p-1)(q-r)+(q-1)(r-p)+(r-1)(p-q)]D
= x0.R0
= 1.1
= 1
Share your thoughts in the comments
Please Login to comment...