Class 11 NCERT Solutions- Chapter 7 Permutations And Combinations – Miscellaneous Exercise on Chapter 7

Question 1. How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER?

Solution:

In the word “DAUGHTER”, there are 3 vowels, namely, A, U, E, and 5 consonants, namely, D, G, H, T, R.

The number of ways of selecting 2 vowels out of 3 = ³C₂ = 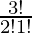 = 3.

The number of ways of selecting 3 consonants out of 5 = ⁵C₃ = 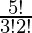 =10.

Therefore, the number of combinations of 2 vowels and 3 consonants is 3 x 10 = 30.

Now, each of these 30 combinations has 5 letters which can be arranged among themselves in 5! ways. 

Therefore, the required number of different words is 30 x 5! = 30 x 120 = 3600

Question 2. How many words, with or without meaning, can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?

Solution:

There are 8 different letters in the word “EQUATION”, in which there are 5 vowels, namely, A, E, I, O and U and 3 consonants, namely, Q, T and N. Since the vowels and consonants have to occur together, assume all vowels as one object (AEIOU) and all consonants as another (QTN). So, there are 2 objects now.

Then, permutations of these 2 objects taken all at a time = ²P₂ = 2! =2.

Within vowel group, we have 5! Possible permutations and 3! permutations within the consonants group.

Hence, the required number of permutations = 2! x 5! x 3! = 1440.

Question 3. A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of: (i) exactly 3 girls ? (ii) atleast 3 girls ? (iii) atmost 3 girls ?

Solution: 

(i) We have to select 7 members from 13 (9 boys + 4 girls). 

If there are exactly 3 girls in each combination, then

The number of ways of selecting 3 girls out of 4 = ⁴C₃ = 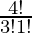 = 4

The number of ways of selecting 4 boys out of 9 = ⁹C₄ = 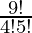 = 126

Hence, total number of ways to form committee with exactly 3 girls = 126 x 4 = 504

(ii) Since, the team has to consist of at least 3 girls, the team can consist of 

3 girls and 4 boys, or 4 girls and 3 boys.

Case 1: The team can consist of 3 girls and 4 boys:

So, from(i), we have,

Total number of ways to select 3 girls and 4 boys = 126 x 4 = 504

Case 2: The team can consist of 4 girls and 3 boys:

Total number of ways to select 4 girls and 3 boys = ⁴C₄ x ⁹C₃ = 1 x 84 = 84

Therefore, total number of ways to form a committee with at least 3 girls = 504 + 84 = 588 

(iii) Since, the team has to consist of at most 3 girls, the team can consist of

3 girls and 4 boys, or 2 girls and 5 boys, or 1 girl and 6 boys, or 7 boys

Case 1: The team can consist of 3 girls and 4 boys

Total number of ways to select 3 girls and 4 boys = 126 x 4 = 504

Case 2: The team can consist of 2 girls and 5 boys

Total number of ways to select 2 girls and 5 boys = ⁴C₂ x ⁹C₅ =  = 126 x 6 = 756

Case 3: The team can consist of 1 girl and 6 boys

Total number of ways to select 1 girl and 6 boys = ⁴C₁ x ⁹C₆ =  = 84 x 4 = 336

Case 4: The team can consist of 7 boys

The number of ways of selecting 7 boys out of 9 = ⁹C₇ = 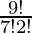 = 36

Therefore, total number of ways to form a committee with at most 3 girls = 504 + 756 + 336 + 36 = 1632

Question 4. If the different permutations of all the letter of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?

Solution:

In a dictionary, words are in ascending order. Hence, for this scenario, all the words starting with A will come before first word starting with E. 

To get the number of words starting with A, we fix the letter A at the extreme left position and then rearrange the remaining 10 letters taken all at a time.  These 10 letters includes I and N 2 times.

Hence, the number of words starting with A = 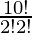 = 907200. 

Hence, 907200 words are there in the list before the first word starting with E.

Question 5. How many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7, and 9 which are divisible by 10, and no digit is repeated?

Solution:

We know that, a number is divisible by 10 if it has 0 at its unit place. Hence, 0 will be fixed at last place in a number. 

The remaining 5 places can be filled by any digit 1, 3, 5, 7 or 9. These 5 digits can be arranged at 5 places in ⁵P₅ = 5! ways.

Hence, 6-digit numbers that can be formed which are divisible by 10 = 5! = 120.

Question 6. The English alphabet has 5 vowels and 21 consonants. How many words with two different vowels and 2 different consonants can be formed from the alphabet?

Solution:

We have to select 2 vowels from 5 and 2 consonants from 21.

The number of ways to select 2 vowels from 5 = ⁵C₂ =  = 10

The number of ways to select 2 consonants from 21 = ²¹C₂ = 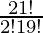 = 210

Permutations of these 4 alphabets taken all at a time = ⁴P₄ = 4! = 24.

Hence, number of words can be formed with 2 different vowels and 2 different consonants = 10 x 210 x 24 = 50400

Question 7. In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?

Solution:

Since, it is required to attempt at least 3 questions from each part, questions selection can be  

Case 1: (3, 5), or (b)(4, 4), or (c) (5, 3) ……(Part I questions, Part 2 questions)

Part I consists of 5 questions and Part II consists of 7 questions.

So, Number of ways to select 3 questions from Part I = ⁵C₃ = 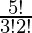 = 10

Number of ways to select 5 questions from Part II = ⁷C₅ = 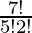 = 21  

Hence, total number of ways for this type of question selection = 10 x 21 = 210

Case 2: Number of ways to select 4 questions from Part I = ⁵C₄ = 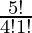 = 5

Number of ways to select 4 questions from Part II = ⁷C₄ = 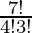 = 35

Hence, total number of ways for this type of question selection = 5 x 35 = 175

Case 3: Number of ways to select 5 questions from Part I = ⁵C₅ = 1

Number of ways to select 3 questions from Part II = ⁷C₃ = 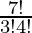 = 35

Hence, total number of ways for this type of question selection = 1 x 35 = 35

Therefore, a student can select the questions in 210 + 175 + 35 = 420 ways.

Question 8. Determine the number of 5-card combinations out of a deck of 52 cards if each selection of 5 cards has exactly one king.

Solution: 

We have to select 5 cards from 52 cards. If there is exactly one king in each combination, then

Case 1: We have to select 1 king card from 4 king cards

Number of ways to select king card = ⁴C₁ =  = 4

Case 2: We have to select 5 – 1 = 4 cards from remaining 52 – 4 = 48 cards

Number of ways to select remaining 4 cards = ⁴⁸C₄ = 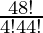 = 194580

And, hence required total number of 5 card combinations = 4 x 194580 = 778320.

Question 9. It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible?

Solution:

There are 5 men and 4 women. Women occupy the even places. Hence, the possible seating arrangement of men and women will be MWMWMWMWM where M denotes Man and W denotes Woman.

Now, 4 women can occupy 4 even places in ⁴P₄ = 4! ways.

And, 5 men can occupy 5 odd places in ⁵P₅ = 5! ways.

Hence, Total number of such possible arrangements: 

5! x 4! = 5 x 4 x 3 x 2 x 1 x 4 x 3 x 2 x 1 = 2880.

Question 10. From a class of 25 students, 10 are to be chosen for an excursion party. There are 3 students who decide that either all of them will join or none of them will join. In how many ways can the excursion party be chosen?

Solution:

According to those 3 students who decide to either join all of them or join none of them, there are 2 cases for excursion party member selection:

Case 1: Do not select those 3 students. 

Hence, select 10 students from remaining 25 – 3 = 22 students.

The number of ways to do this = ²²C₁₀ = 646646

Case 2: Select those 3 students. 

This means, we are short of 7 students and these can be selected from remaining 25 – 3 = 22 students.

The number of ways to do this = ²²C₇ x ³C₃ = 170544

Hence, required number of ways to choose excursion party:

646646 + 170544 = 817190

Question 11. In how many ways can the letters of the word ASSASSINATION be arranged so that all the S’s are together?

Solution:

Word “ASSASSINATION” has 4 S. We have to place all S’s together. Hence, we will assume group of 4 S as a single object. This single object together with 9 remaining letters (objects) will be counted as 10 objects to be arranged. These include 3 A’s, 2 I’s and N’s and 1 T and O. 

So, required number of ways = 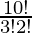 = 151200