Class 11 RD Sharma Solutions – Chapter 23 The Straight Lines – Exercise 23.4
Last Updated :
18 Mar, 2021
Question 1. Find the equation of straight line passing through the point (6, 2) and having slope -3.
Solution:
We know (y – y1) = m(x – x1)
Here, m = Slope of line = -3
x1 = 6, y1 = 2
So, the equation of line is
⇒ y – 2 = (-3)(x – 6)
⇒ y – 2 = -3x + 18
⇒ 3x + y – 20 = 0
Question 2. Find the equation of straight line passing through (-2, 3) and inclined at an angle of 45° with the x-axis.
Solution:
We know y – y1 = m(x – x1)
Here, m = Slope of line = tan 45° = 1
x1 = -2, y1 = 3
So, the equation of line is
⇒ y – 3 = 1(x – (-2))
⇒ y – 3 = x + 2
⇒ x – y + 5 = 0
Question 3. Find the equation of straight line which divides the join of points (2, 3) and (-5, 8) in the ratio 3:4 and is also perpendicular to it.
Solution:
Let the point at which the line divides the join of points (2, 3) and (-5, 8) in the ratio 3:4 be P(x1, y1)
P(x1, y1) = \frac{(4 × 2 - 5 × 3)}{(3 + 4)}, \frac{(4 × 3 + 3 × 8)}{(3+4)}
= (-1, 36/7)
Slope of the given points=(8-3)/(-5-2) =-5/7
Since, the required line is perpendicular to the line joining the given points.
Therefore, the slope of required line ‘m’ = 7/5
Here, x1 = -1, y1 = 36/7 & m = 7/5
So, the equation of line is
⇒ y – 36/7 = 7/5(x – (-1))
⇒ y-36/7 = 7/5(x + 1)
⇒ 35y – 180 = 49x + 49
⇒ 49x + 35y + 229 = 0 is the required equation of straight line.
Question 4. Prove that the perpendicular drawn from the point (4, 1) on the join of (2, -1) and (6, 5) divides it in ratio 5:8.
Solution:
Let PO be the perpendicular drawn from P(4,1) on the line joining A(2, -1) and B(6, 5)
Let slope of PO be ‘m’
According to question
m × Slope of AB = -1
⇒ m × (5 + 1)/(6 – 2) = -1
⇒ m × 6/4 = -1
⇒ m = -4/6 = -2/3
Thus, the equation of line PO
x1 = 4, y1 = 1 & m = -2/3
(y – 1) = -2/3(x – 4)
⇒ 3y – 3 = -2x + 8
⇒ 2x + 3y – 11 = 0 ——–(1)
Let O divide the line AB in the ratio of K:1
Then the coordinates of O are \frac{(6k + 2)}{(k + 1)}, \frac{(5k - 1)}{(k + 1)}
Since point O lies in the line AB
Therefore, it satisfies the equation (1)
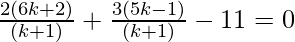
⇒ 12k + 4 + 15k – 3 – 11(k + 1) = 0
⇒ 27k – 11k + 1 – 11 = 0
⇒ 16k = 10
⇒ k = 5/8
Hence Proved
Question 5. Find the equation to the altitudes of the triangle whose angular points are A(2, -2), B(1, 1), and C(-1, 0).
Solution:
Let the altitudes be AE, BF and CD

Slope of AE × Slope of BC = -1 [Since both lines are perpendicular to each other]
Slope of AE = (-1) / Slope of BC
Slope of AE = 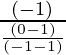
= 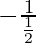
= -2
Equation of the altitude AE
y – (-2) = (-2)(x – 2)
⇒ y + 2 = -2x + 4
⇒ 2x + y – 2 = 0
Similarly,
Slope of BF × Slope of AC = -1
Slope of BF = ![Rendered by QuickLaTeX.com \frac{(-1)}{[\frac{(0 - (-2))}{(-1 - 2)}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a404a2e99dc7185936f5b8b3e95aea4a_l3.png)
= 
= 3/2
Equation of the altitude BF
y – 1 = (3/2)(x – 1)
⇒ 2(y – 1) = 3x – 3
⇒ -3x + 2y – 2 + 3 = 0
⇒ 3x – 2y – 1 = 0
Slope of CD × Slope of AB = -1
Slope of CD= 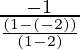
= 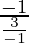
= 1/3
Equation of the altitude CD
y – 0 = (1/3) (x – (-1))
⇒ 3y = x + 1
⇒ x – 3y + 1 = 0
Question 6. Find the equation of the right bisector of the line segment joining the points (3, 4) and (-1, 2).
Solution:
Let the points of the line segment be A(3, 4) and B(-1, 2)
Let the right bisector meet at point ‘P’ on the line segment
Coordinates of point P = \frac{(3-1)}{2}, \frac{(4+2)}{2} [Using the mid point formula]
= (1, 3)
Slope of AB = [(2 – 4) / (-1 – 3)]
=-2/-4
= 1/2
Slope of right bisector = 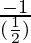
= -2
Equation of the right bisector
⇒ y – 3 = -2(x – 1)
⇒ y – 3 = -2x + 2
⇒ 2x + y – 5 = 0 is the required equation of the right bisector
Question 7. Find the equation of the straight line passing through the point (3, -2) and making an angle of 60° with the positive direction y-axis.
Solution:
Since the line is making an angle of 60° with the positive direction of y-axis i
t makes an angle of 30° with the positive direction of x-axis as shown in the diagram.
Slope of line ‘m’= tan 30° = 1/√3
Equation of straight line passing through (3, -2)
y – (-2) = 1/√3(x – 3)
⇒ √3(y + 2) = x – 3
⇒ √3y + 2√3 = x – 3
⇒ x – √3y – 3 – 2√3 = 0 is the required equation of straight line.
Question 8. Find the equation of the straight line which passes through the point (1, 2) and makes an angle with the positive direction of x-axis whose sine is 3/5.
Solution:
Given, sin θ = 3/5
tan θ = 3/√(25 – 9) = 3/4
Slope of the line m = 3/4
Equation of straight line passing through (1, 2)
y – 2 = 3/4(x – 1)
⇒ 4(y – 2) = 3x – 3
⇒ 4y – 8 = 3x – 3
⇒ 3x – 4y + 5 = 0 is the required equation of straight line.
Question 9. Find the equation of the line passing through the point (-3, 5) and perpendicular to the line joining (2, 5) and (-3, 6).
Solution:
Slope of the required equation ‘m’ = (-1) / [Slope of line joining (2, 5) and (-3, 6)] [Perpendicular to each other]
m =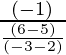
m = 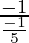
m = 5
Equation of straight line passing through (-3, 5)
y – 5 = 5(x – (-3))
⇒ y – 5 = 5x + 15
⇒ 5x – y + 20 = 0 is the required equation of straight line.
Question 10. Find the equation of the right bisector of the line segment joining the points A(1, 0) and B(2, 3).
Solution:
Let the right bisector meet at point ‘P’ on the line segment
Coordinates of point P = [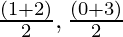 ] [Using the mid point formula]
] [Using the mid point formula]
= (3/2, 3/2)
Slope of AB = [(3 – 0)/(2 – 1)]
= 3/1 = 3
Slope of right bisector = -1/3
Equation of the right bisector
⇒ y – 3/2 = -1/3(x – 3/2)
⇒ 3(y – 3/2) = -x + 3/2
⇒ x + 3y – 9/2 – 3/2 = 0
⇒ x + 3y – 6 = 0
⇒ x + 3y – 6 = 0 is the required equation of the right bisector.
Question 11. Find the lines through the point (0, 2) making angles π/3 and 2π/3 with the x-axis. Also, find the lines parallel to them cutting the y-axis at a distance of 2 units below the origin.
Solution:
Given the line through the point (0, 2) making angles π/3 and 2π/3 with the x-axis
.Slope m1= tan π/3 = √3
Slope m2 = tan 2π/3 = -√3
Equation of the required lines
⇒ y – 2 = √3(x – 0) and y – 2 = -√3(x – 0)
⇒ y – √3x – 2 = 0 and y + √3x – 2 = 0
Now, the equation of the line parallel to the line having slope m1 and y intercept c= -2
y = m1x + c
⇒ y = √3x – 2
Similarly, the equation of the line parallel to the line having slope m2 and y intercept c = -2
y= m2x + c
⇒ y = -√3x – 2
Question 12. Find the equation of the straight lines which cut off an intercept 5 from the y-axis and are equally inclined to the axes.
Solution:
Given that the straight lines cut off an intercept 5 from the y-axis and are equally inclined to the axes.

Slope of the two lines are m1= tan 45° =1 and m2 = tan 135° = -1
Equation of the required straight lines are
y = m1x + c or y = m2 + c
⇒ y = x +5 or y = -x + 5
⇒ y = x +5 or y + x = 5
Question 13. Find the equation of straight lines which intercepts a length 2 on the positive direction of the x-axis and is inclined at an angle of 135° with the positive direction of y-axis.
Solution:
The required line which is inclined at an angle of 135° with the positive direction of y-axis makes an angle of 45° with the positive x-axis.
Slope of the required line m = tan 45° = -1
Equation of the required straight line with x-intercept c = 2 and m = -1
x = my + c
⇒ x = 1y + 2
⇒ x – y – 2 = 0
Question 14. Find the equation of line passing through (0, 0) with slope m.
Solution:
Equation of line passing through (0, 0) with slope m is
y – 0 = m(x – 0)
⇒ y = mx
Question 15. Find the equation of line passing through (2, 2√3) and inclined with x-axis at an angle of 75°.
Solution:
Slope of the line m = tan 75°
= tan (45° + 30°)
= (tan 45° + tan30°) /(1 – tan 45° tan30°)
= (1 + 1/√3)/(1 – 1/√3)
m = (√3 + 1)/(√3 – 1) = 2 + √3
Equation of the required line passing through (2, 2√3) with slope of 2 + √3
y – 2√3 = (2 + √3)(x – 2)
⇒ y – 2√3 = (2 + √3)x – 4 – 2√3
⇒ (2 + √3)x – y – 4 = 0
Question 16. Find the equation of the line passing through(1, 2) and making angle of 30° with the y-axis.
Solution:
Let us considered an equation of line passing through points(x1, y1) which making an angle θ with x-axis.
(y – y1) = tanθ(x – x1) -(1)
Given: Point = (1, 2), and angle = 30°(with y-axis)
So, angle with x-axis = 90° – 30° = 60°
Now put all these values in eq(1), we get
(y – 2) = tan60°(x – 1)
(y – 2) = √3(x – 1)
y – 2 = √3x – √3
√3x – √3 – y + 2 = 0
√3x – y – √3 + 2 = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...