Class 11 RD Sharma Solutions- Chapter 16 Permutations – Exercise 16.3 | Set 1
Last Updated :
09 Mar, 2022
Question 1. Evaluate each of the following:
(i) 8P3
(ii) 10P4
(iii) 6P6
(iv) P (6, 4)
Solution:
(i) 8P3
As we know that, 8P3 can be written as P (8, 3)
After applying the formula,
P (n, r) = 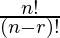
P (8, 3) 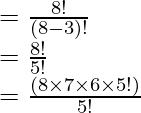
= 8 × 7 × 6
= 336
∴ 8P3 = 336
(ii) 10P4
As we know that, 10P4 can be written as P (10, 4)
After applying the formula,
P (n, r) = 
P (10, 4) = 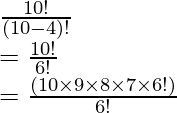
= 10 × 9 × 8 × 7
= 5040
∴ 10P4 = 5040
(iii) 6P6
As we know that, 6P6 can be written as P (6, 6)
After applying the formula,
P (n, r) = 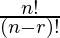
P (6, 6) = 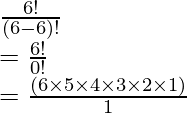 {Since, 0! = 1}
{Since, 0! = 1}
= 6 × 5 × 4 × 3 × 2 × 1
= 720
∴ 6P6 = 720
(iv) P (6, 4)
After applying the formula,
P (n, r) = 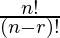
P (6, 4) = 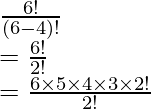
= 6 × 5 × 4 × 3
= 360
∴ P (6, 4) = 360
Question 2. If P (5, r) = P (6, r – 1), find r.
Solution:
Given:
P (5, r) = P (6, r – 1)
After applying the formula,
P (n, r) = 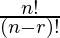
P (5, r) = 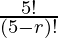
P (6, r-1) = 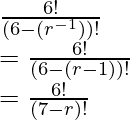
So, from the question,
P (5, r) = P (6, r – 1)
So, after substituting the values in above expression we will get,
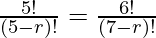
Upon evaluating,
![Rendered by QuickLaTeX.com \frac{(7-r)!}{(5-r)!}=\frac{6!}{5!}\\ \frac{[(7-r)(7-r-1)(7-r-2)!]}{(5-r)!}=\frac{(6\times5!)}{5!}\\ \frac{[(7-r)(6-r)(5-r)!]}{(5-r)!}=6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b57eab3c306a4ced71cfca075aa0b2be_l3.png)
(7 – r) (6 – r) = 6
42 – 6r – 7r + r2 = 6
42 – 6 – 13r + r2 = 0
r2 – 13r + 36 = 0
r2 – 9r – 4r + 36 = 0
r(r – 9) – 4(r – 9) = 0
(r – 9) (r – 4) = 0
r = 9 or 4
For, P (n, r): r ≤ n
∴ r = 4 [for, P (5, r)]
Question 3. If 5 P(4, n) = 6 P(5, n – 1), find n.
Solution:
Given:
5 P(4, n) = 6 P(5, n – 1)
After applying the formula,
P (n, r) = 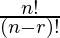
P (4, n) = 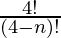
P (5, n-1) = 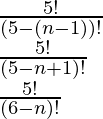
So, from the question,
5 P(4, n) = 6 P(5, n – 1)
So, after substituting the values in above expression we will get,
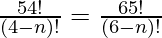
Upon evaluating,
![Rendered by QuickLaTeX.com \frac{(6 - n)!}{(4 - n)!}= \frac{6}{5} × \frac{5!}{4!}\\ \frac{[(6 - n) (6 - n - 1) (6 - n - 2)!]}{(4 - n)!} = \frac{(6 × 5 × 4!)}{ (5 × 4!)}\\ \frac{[(6 - n) (5 - n) (4 - n)!]}{(4 - n)!} = 6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa65f166dbe84a75808daf2b328d9db8_l3.png)
(6 – n) (5 – n) = 6
30 – 6n – 5n + n2 = 6
30 – 6 – 11n + n2 = 0
n2 – 11n + 24 = 0
n2 – 8n – 3n + 24 = 0
n(n – 8) – 3(n – 8) = 0
(n – 8) (n – 3) = 0
n = 8 or 3
For, P (n, r): r ≤ n
∴ n = 3 [for, P (4, n)]
Question 4. If P(n, 5) = 20 P(n, 3), find n.
Solution:
Given:
P(n, 5) = 20 P(n, 3)
After applying the formula,
P (n, r) = 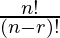
P (n, 5) = 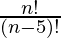
P (n, 3) = 
So, from the question,
P(n, 5) = 20 P(n, 3)
After substituting the values in above expression we will get,
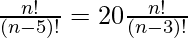
Upon evaluating,
![Rendered by QuickLaTeX.com \frac{n! (n - 3)!}{n! (n - 5)!} = 20\\ \frac{[(n - 3) (n - 3 - 1) (n - 3 - 2)!]} {(n - 5)!} = 20\\ \frac{[(n - 3) (n - 4) (n - 5)!]}{(n - 5)!} = 20](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd32a59c1a73b7535f49452220651b48_l3.png)
(n – 3) (n – 4) = 20
n2 – 3n – 4n + 12 = 20
n2 – 7n + 12 – 20 = 0
n2 – 7n – 8 = 0
n2 – 8n + n – 8 = 0
n(n – 8) – 1(n – 8) = 0
(n – 8) (n – 1) = 0
n = 8 or 1
For, P(n, r): n ≥ r
∴ n = 8 [for, P(n, 5)]
Question 5. If nP4 = 360, find the value of n.
Solution:
Given:
nP4 = 360
nP4 can be written as P (n , 4)
After applying the formula,
P (n, r) = 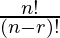
P (n, 4) = 
So, from the question,
nP4 = P (n, 4) = 360
After substituting the values in above expression we will get,
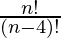 = 360
= 360
![Rendered by QuickLaTeX.com \frac{[n(n - 1) (n - 2) (n - 3) (n - 4)!]} {(n - 4)!}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-61de08050021d0b204a6174e1502df50_l3.png) = 360
= 360
n (n – 1) (n – 2) (n – 3) = 360
n (n – 1) (n – 2) (n – 3) = 6×5×4×3
Upon comparing,
The value of n is 6.
Question 6. If P(9, r) = 3024, find r.
Solution:
Given:
P (9, r) = 3024
After applying the formula,
P (n, r) = 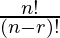
P (9, r) = 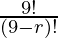
So, from the question,
P (9, r) = 3024
Substituting the obtained values in above expression we get,
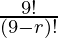 = 3024
= 3024
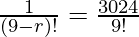
= 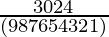
= 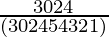
= 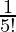
(9 – r)! = 5!
9 – r = 5
-r = 5 – 9
-r = -4
∴ The value of r is 4.
Question 7. If P (11, r) = P (12, r – 1), find r.
Solution:
Given:
P (11, r) = P (12, r – 1)
After applying the formula,
P (n, r) = 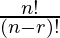
P (11, r) = 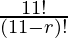
P (12, r-1) = 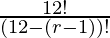
= 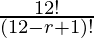
= 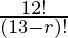
So, from the question,
P (11, r) = P (12, r – 1)
After substituting the values in above expression we will get,
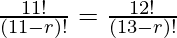
Upon evaluating,
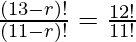
![Rendered by QuickLaTeX.com \frac{[(13 - r) (13 - r - 1) (13 - r - 2)!] }{(11 - r)!} = \frac{(12×11!)}{11!}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f0ad9f5c2e00dc320c19de71b80eaf72_l3.png)
![Rendered by QuickLaTeX.com \frac{[(13 - r) (12 - r) (11 -r)!] }{(11 - r)! }](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3adccbd8611f9d6bed750622206db62c_l3.png) = 12
= 12
(13 – r) (12 – r) = 12
156 – 12r – 13r + r2 = 12
156 – 12 – 25r + r2 = 0
r2 – 25r + 144 = 0
r2 – 16r – 9r + 144 = 0
r(r – 16) – 9(r – 16) = 0
(r – 9) (r – 16) = 0
r = 9 or 16
For, P (n, r): r ≤ n
∴ r = 9 [for, P (11, r)]
Question 8. If P(n, 4) = 12. P(n, 2), find n.
Solution:
Given:
P (n, 4) = 12. P (n, 2)
After applying the formula,
P (n, r) = 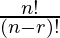
P (n, 4) = 
P (n, 2) = 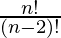
So, from the question,
P (n, 4) = 12. P (n, 2)
After substituting the values in above expression we will get,
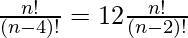
Upon evaluating,
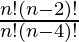 = 12
= 12
![Rendered by QuickLaTeX.com \frac{[(n - 2) (n - 2 -1) (n - 2 - 2)!] }{(n - 4)! }](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4e88e6ec53b286b1147708a641065406_l3.png) = 12
= 12
![Rendered by QuickLaTeX.com \frac{[(n - 2) (n - 3) (n - 4)!] }{ (n - 4)!}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0160c89a164b453760695ab6007c4c40_l3.png) = 12
= 12
(n – 2) (n – 3) = 12
n2 – 3n – 2n + 6 = 12
n2 – 5n + 6 – 12 = 0
n2 – 5n – 6 = 0
n2 – 6n + n – 6 = 0
n (n – 6) – 1(n – 6) = 0
(n – 6) (n – 1) = 0
n = 6 or 1
For, P (n, r): n ≥ r
∴ n = 6 [for, P (n, 4)]
Question 9. If P(n – 1, 3) : P(n, 4) = 1 : 9, find n.
Solution:
Given:
P (n – 1, 3): P (n, 4) = 1 : 9
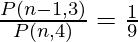
After applying the formula,
P (n, r) = 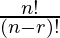
P (n – 1, 3) = 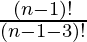
= 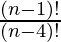
P (n, 4) = 
So, from the question,

After substituting the values in above expression we will get,
![Rendered by QuickLaTeX.com \frac{\frac{[(n - 1)!}{ (n - 4)!]}} { \frac{[n!}{(n - 4)!]}} = \frac{1}{9}\\ \frac{[(n - 1)! }{ (n - 4)!]} × \frac{[(n - 4)! }{ n!]} = \frac{1}{9}\\ \frac{(n - 1)!}{n!} = \frac{1}{9}\\ \frac{(n - 1)!}{n (n - 1)!} = \frac{1}{9}\\ \frac{1}{n} = \frac{1}{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-39129ec1339d8399d601869706f1fb05_l3.png)
n = 9
∴ The value of n is 9.
Question 10. If P(2n – 1, n) : P(2n + 1, n – 1) = 22 : 7 find n.
Solution:
Given:
P(2n – 1, n) : P(2n + 1, n – 1) = 22 : 7
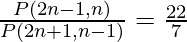
After applying the formula,
P (n, r) =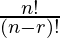
P (2n – 1, n) =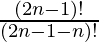
= 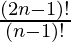
P (2n + 1, n – 1) = 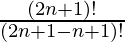
= 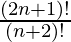
So, from the question,
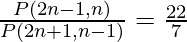
After substituting the values in above expression we will get,
![Rendered by QuickLaTeX.com \frac{\frac{(2n - 1)! }{ (n - 1)!} }{\frac{ (2n + 1)! }{ (n + 2)!}} = \frac{22}{7}\\ \frac{(2n - 1)! }{ (n - 1)!} × \frac{(n + 2)! }{ (2n + 1)!} = \frac{22}{7}\\ \frac{(2n - 1)! }{ (n - 1)!} × \frac{[(n + 2) (n + 2 - 1) (n + 2 - 2) (n + 2 - 3)!] }{ [(2n + 1) (2n + 1 - 1) (2n + 1 - 2)]} = \frac{22}{7}\\ \frac{[(2n - 1)! }{ (n - 1)!]} × \frac{[(n + 2) (n + 1) n(n - 1)!] }{ [(2n + 1) 2n (2n - 1)!]} = \frac{22}{7}\\ \frac{[(n + 2) (n + 1)] }{ (2n + 1)2} = \frac{22}{7}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-97faef314bd6636b7a028ac4bb471bdd_l3.png)
7(n + 2) (n + 1) = 22×2 (2n + 1)
7(n2 + n + 2n + 2) = 88n + 44
7(n2 + 3n + 2) = 88n + 44
7n2 + 21n + 14 = 88n + 44
7n2 + 21n – 88n + 14 – 44 = 0
7n2 – 67n – 30 = 0
7n2 – 70n + 3n – 30 = 0
7n(n – 10) + 3(n – 10) = 0
(n – 10) (7n + 3) = 0
n = 10, 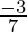
As we know that, n ≠ 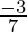
∴ The value of n is 10.
Share your thoughts in the comments
Please Login to comment...