Class 11 RD Sharma Solutions – Chapter 32 Statistics – Exercise 32.7

Last Updated : 03 Mar, 2021

Question 1. Two plants A and B of a factory show the following results about the number of workers and the wages paid to them

	Plant A	Plant B
No. of workers	5000	6000
Average monthly wages	₹2500	₹2500
The variance of distribution of wages	81	100

In which plant A or B is there greater variability in individual wages?

Solution:

Variation of the distribution of wages in plant A (σ² =18)

So, Standard deviation of the distribution A (σ – 9)

Similarly, the Variation of the distribution of wages in plant B (σ² =100)

So, Standard deviation of the distribution B (σ – 10)

And, Average monthly wages in both the plants is 2500,

Since, the plant with a greater value of SD will have more variability in salary.

∴ Plant B has more variability in individual wages than plant A

Question 2. The means and standard deviations of heights and weights of 50 students in a class are as follows:

	Weights	Heights
Mean	63.2 Kg	63.2 inch
Standard deviation	5.6 Kg	11.5 inch

Which shows more variability, heights or weights?

Solution:

We observe that the average weights and height for the 50 students is same i.e. 63.2.

Therefore, the parameter with greater variance will have more variability.

Thus, height has greater variability

Question 3. The coefficient of variation of two distribution are 60% and 70%, and their standard deviations are 21 and 16 respectively. What is their arithmetic means?

Solution:

Coefficient of variation = 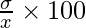$\frac{\sigma}{x}\times100$

So, we have:

$60\% =\frac{21}{\overline{x}}\times100\Rightarrow\overline{x}=\frac{21}{.60}\times100=35\\ 70\% =\frac{16}{\overline{x}}\times100\Rightarrow\overline{x}=\frac{16}{.70}\times100=22.85\\$

∴ Means are 35 and 22.85

Question 4. Calculate coefficient of variation from the following data:

Income(in ₹):	1000 – 1700	1700 – 2400	2400 – 3100	3100 – 3800	3800 – 4500	4500 – 5200
No. of families:	12	18	20	25	35	10

Solution:

Class

F_i

x_i

$U_i=\frac{x_i-mean}{700}$

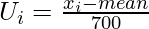
f_iu_i

f_iu_i²

1000 – 1700

12

1350

-2

-24

48

1700 – 2400

18

2050

-1

-18

18

2400 – 3100

20

2750

0

0

0

3100 – 3800

25

3450

1

25

25

3800 – 4500

35

4150

2

70

140

4500 – 5200

10

4850

3

30

90

$\sum f_i=120$

$\sum u_if_i=83$

$\sum u_i^2f_i=321$

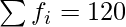
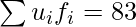
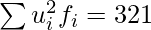
Now,

N = 120, $\sum u_i^2f_i=321$

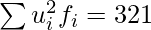
Mean, $\overline{X}=A+h\left(\frac{\sum u_if_i}{N}\right)\\ \overline{X}=2750+700\left(\frac{83}{120}\right)\\ =3234.17\\ Var(X)=h^2\left[\frac{1}{N}\displaystyle\sum_{i=1}^nf_iu_i^2-\left(\frac{1}{N}\sum_{i=1}^nu_if_i\right)^2\right]\\ Var(X)=490000\left[\left(\frac{321}{120}\right)-\left(\frac{83}{120}\right)^2\right]$

Variance = 1076332.64

Standard Deviation, 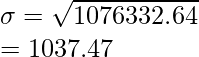$\sigma=\sqrt{1076332.64}\\ =1037.47$

Coefficient of variation = 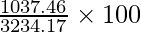$\frac{1037.46}{3234.17}\times100$

= 32.08

∴ The coefficient variation is 32.08

Question 5. An analysis of the weekly wages paid to workers in two firms A and B, belonging to the same industry gives the following results:

	Firm A	Firm B
No. of wage earners	586	648
Average weekly wages	₹52.5	₹47.5
The variance of the distribution of wages	100	121

(i) Which firm A or B pays out the larger amount as weekly wages?

(ii) Which firm A or B has greater variability in individual wages?

Solution:

(i) Average weekly wages = 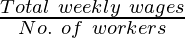$\frac{Total\ weekly\ wages}{No.\ of\ workers}$

Total weekly wages = (Average weekly wages) × (No. of workers)

Total weekly wages of Firm A = 52.5 × 586 = Rs 30765

Total weekly wages of Firm B = 47.5 × 648 = Rs 30780

Firm B pays a larger amount as Firm A

(ii) Here,

S.D (Firm A) = 10 and S.D (Firm B) = 11

Coefficient variance (Firm A) = $\frac{10}{52.5}\times100$

= 19.04

Coefficient variance (Firm B) = $\frac{11}{47.5}\times100$

= 23.15

∴ Coefficient variance of Firm B is greater than that of Firm A, Firm B has greater variability in individual wages.

Question 6. The following are some particulars of the distribution of weights of boys and girls in a class:

	Boys	Girls
Number	100	50
Mean weight	60 Kg	45 Kg
Variance	9	4

Which of the distributions is more variable?

Solution:

Given:

S.D (Boys) is 3 and S.D (Girls) is 2

Coefficient variance (Boys) = 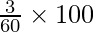$\frac{3}{60} \times 100$

= 5

Coefficient variance (Girls) = 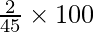$\frac{2}{45} \times 100$

= 4.4

∴ Coefficient variance of Boys is greater than Coefficient variance of girls, and then the distribution of weights of boys is more variable than that of girls.

Question 7. The mean and standard deviation of marks obtained by 50 students of a class in three subjects, mathematics, physics and chemistry are given below:

Subject

Mean

Mathematics

Physics

Chemistry

40.9

Standard deviation

Solution:

In order to compare the variability of marks in Math, Physics and Chemistry.

We have to calculate their coefficient of variation.

Let σ₁, σ₂ and σ₃ denote the standard deviation of marks in Math, Physics and Chemistry respectively. Further, Let 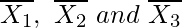$\overline{X_1},\ \overline{X_2}\ and\ \overline{X_3}$ be the mean scores in Math, Physics and Chemistry respectively.

We have

$\overline{X_1}=42\ \ \ \ \ \overline{X_2}=32\ \ \ \ \ \overline{X_3}=40.9$

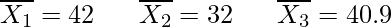
⇒ σ₁ = 12 σ₂ = 15 σ₃ = 20

Now,

Coefficient of variation in Maths = 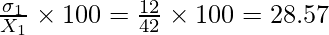$\frac{\sigma_1}{X_1}\times100=\frac{12}{42}\times100=28.57$

Coefficient of variation in Physics = $\frac{\sigma_2}{X_2}\times100=\frac{15}{32}\times100=46.88$

Coefficient of variation in Chemistry = 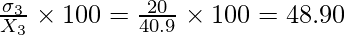$\frac{\sigma_3}{X_3}\times100=\frac{20}{40.9}\times100=48.90$

Clearly, coefficient of variation in marks is greatest in Chemistry and lowest in Math.

So, marks in chemistry show highest variability and marks in maths show lowest variability.

Question 8. From the data given below state which group is more variable, G₁ or G₂?

Marks

Group G₁

10 – 20

20 – 30 30 – 40

17 32

40 – 50

50 – 60 60 – 70

40 10

70 – 80

Group G₂

20 30

43 15

Solution:

Let’s first find the coefficient of variable for group G₁

CI f

  10 – 20 9

20 – 30 17

x u=(x – A)/h

15 -3

25 -2

fu u²

-27 9

-34 4

fu²

   81

68

30 – 40 32

40 – 50 33

35 -1

45 0

-32 1

0 0

32

0

50 – 60 40 55 1 40 1 40

60 – 70 10

70 – 80 9

65 2

75 3

20 4

27 9

40

81

  150 -6 342

Here, N = 150, A = 45, 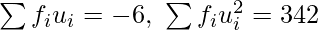$\sum f_iu_i=-6,\ \sum f_iu_i^2=342$ and h = 10

∴ Mean = $\overline{x}=A+h\left(\frac{1}{N}\sum f_iu_i\right)\\ \overline{x}=45+10\left(\frac{-6}{150}\right)=44.6\\ Var(x)=h^2\left[\frac{1}{N}\sum f_iu_i^2-\left(\frac{1}{N}\sum f_iu_i\right)^2\right]=100\left[\frac{342}{150}-\left(\frac{-6}{150}\right)^2\right]=227.84\\ S.D.=\sqrt{Var(x)}=\sqrt{227.84}=15.09$

Coefficient of variation = 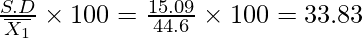$\frac{S.D}{\overline{X_1}}\times100=\frac{15.09}{44.6}\times100=33.83$

Now, lets find the coefficient of variable for group G₂

CI f

10 – 20 10

20 – 30 20

x u=(x – A)/h

15 -3

25 -2

fu u²

-30 9

-40 4

fu²

90

80

30 – 40 30

40 – 50 25

35 -1

45 0

-30 1

0 0

30

0

50 – 60 43 55 1 43 1 43

60 – 70 15

70 – 80 7

65 2

75 3

30 4

21 9

60

63

150 -6 366

Here, N = 150, A = 45, $\sum f_iu_i=-6,\ \sum f_iu_i^2=366$ and h = 10

∴ Mean = $\overline{x}=A+h\left(\frac{1}{N}\sum f_iu_i\right)\\ \overline{x}=45+10\left(\frac{-6}{150}\right)=44.6\\ Var(x)=h^2\left[\frac{1}{N}\sum f_iu_i^2-\left(\frac{1}{N}\sum f_iu_i\right)^2\right]=100\left[\frac{366}{150}-\left(\frac{-6}{150}\right)^2\right]=243.84\\ S.D.=\sqrt{Var(x)}=\sqrt{243.84}=15.62$

Coefficient of variation = 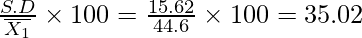$\frac{S.D}{\overline{X_1}}\times100=\frac{15.62}{44.6}\times100=35.02$

Group G₂ is more variable

Question 9. Find the coefficient of variation for the following data:

Size (in cms): 10 – 15	15 – 20	20 – 25	25 – 30	30 – 35	35 – 40
No. of items: 2	8	20	35	20	15

Solution:

  CI f x

10 – 15 2 12.5

15 – 20 8 17.5

u=(x – A)/h fu u²

-2 -4 4

-1 -8 1

fu²

8

8

20 – 25 20 22.5

25 – 30 35 27.5

0 0 0

1 35 1

0

35

30 – 35 20 32.5 2 40 4 80
35 – 40 15 37.5 3 45 9 135
  100   108   266

Here, N = 100, A = 22.5, 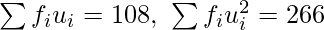$\sum f_iu_i=108,\ \sum f_iu_i^2=266$ and h = 5

∴ Mean = $\overline{x}=A+h\left(\frac{1}{N}\sum f_iu_i\right)\\ \overline{x}=22.5+5\left(\frac{108}{100}\right)=27.90\\ Var(x)=h^2\left[\frac{1}{N}\sum f_iu_i^2-\left(\frac{1}{N}\sum f_iu_i\right)^2\right]=25\left[\frac{266}{100}-\left(\frac{108}{100}\right)^2\right]=37.34\\ S.D.=\sqrt{Var(x)}=\sqrt{37.34}=6.11$

Coefficient of variation = 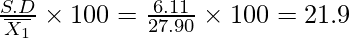$\frac{S.D}{\overline{X_1}}\times100=\frac{6.11}{27.90}\times100=21.9$

Question 10. From the prices of shares X and Y given below: find out which is more stable in value:

X:	35	54	52	53	56	58	52	50	51	49
Y:	108	107	105	105	106	107	104	103	104	101

Solution:

x d = (x – Mean)

  35 -13

  24 -24

d²

169

576

52 4

53 5

16

25

56 8 64

58 10

52 4

100

16

50 2 4
51 3 9
49 1 1
480 980

∴ Mean = $\overline{x}=\frac{1}{n}\sum x_i=\frac{1}{10}[480]=48\\ Var(x)=\frac{1}{n}\left\{\sum (x_i-\overline{x})^2\right\}=\frac{1}{10}(980)=98\\ S.D(x)=\sqrt{Var(x)}=\sqrt{98}=9.9$

Coefficient of variation = 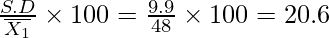$\frac{S.D}{\overline{X_1}}\times100=\frac{9.9}{48}\times100=20.6$

x d = (x – Mean)

  35 -13

24 -24

  d²

   169

576

52 4

53 5

16

25

56 8 64

58 10

52 4

100

16

50 2 4
51 3 9
49 1 1
480 980

∴ Mean = $\overline{x}=\frac{1}{n}\sum x_i=\frac{1}{10}[1050]=105\\ Var(x)=\frac{1}{n}\left\{\sum (x_i-\overline{x})^2\right\}=\frac{1}{10}(40)=4\\ S.D(x)=\sqrt{Var(x)}=\sqrt{4}=2$

Coefficient of variation = 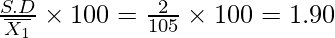$\frac{S.D}{\overline{X_1}}\times100=\frac{2}{105}\times100=1.90$

Since the coefficient of variation for share Y is smaller than the coefficient of variation for shares X, they are more stable.

Suggest improvement

Class 11 RD Sharma Solutions- Chapter 32 Statistics - Exercise 32.6

Class 11 RD Sharma Solutions- Chapter 33 Probability - Exercise 33.1 | Set 1

Share your thoughts in the comments

Class	F_i	x_i	$U_i=\frac{x_i-mean}{700}$	f_iu_i	f_iu_i²
1000 – 1700	12	1350	-2	-24	48
1700 – 2400	18	2050	-1	-18	18
2400 – 3100	20	2750	0	0	0
3100 – 3800	25	3450	1	25	25
3800 – 4500	35	4150	2	70	140
4500 – 5200	10	4850	3	30	90
	$\sum f_i=120$			$\sum u_if_i=83$	$\sum u_i^2f_i=321$

CI f x 10 – 15 2 12.5 15 – 20 8 17.5	u=(x – A)/h fu u² -2 -4 4 -1 -8 1	fu² 8 8
20 – 25 20 22.5 25 – 30 35 27.5	0 0 0 1 35 1	0 35
30 – 35 20 32.5	2 40 4	80
35 – 40 15 37.5	3 45 9	135
100	108	266

x d = (x – Mean) 35 -13 24 -24	d² 169 576
52 4 53 5	16 25
56 8	64
58 10 52 4	100 16
50 2	4
51 3	9
49 1	1
480	980

Chapter 1: Sets

Chapter 2: Relations

Chapter 3: Functions

Chapter 4: Measurement of Angles

Chapter 5: Trigonometric Functions

Chapter 6: Graphs of Trigonometric Functions

Chapter 7: Trigonometric Ratios of Compound Angles

Chapter 8: Transformation Formulae

Chapter 9: Trigonometric Ratios of Multiple and Sub Multiple Angles

Chapter 10: Sine and Cosine Formulae and their Applications

Chapter 11: Trigonometric Equations

Chapter 12: Mathematical Induction

Chapter 13: Complex Numbers

Chapter 15: Linear Inequations

Chapter 16: Permutations

Chapter 17: Combinations

Chapter 18: Binomial Theorem

Chapter 19: Arithmetic Progressions

Chapter 20: Geometric Progressions

Chapter 21: Some Special Series

Chapter 22: Brief Review of Cartesian System of Rectangular Coordinates

Chapter 23: The Straight Lines

Chapter 24: The Circle

Chapter 25: Parabola

Chapter 26: Ellipse

Chapter 27: Hyperbola

Chapter 28: Introduction to 3D Coordinate Geometry

Chapter 29: Limits

Chapter 30: Derivatives

Chapter 31: Mathematical Reasoning

Chapter 32: Statistics

Chapter 33: Probability

Chapter 1: Sets

Chapter 2: Relations

Chapter 3: Functions

Chapter 4: Measurement of Angles

Chapter 5: Trigonometric Functions

Chapter 6: Graphs of Trigonometric Functions

Chapter 7: Trigonometric Ratios of Compound Angles

Chapter 8: Transformation Formulae

Chapter 9: Trigonometric Ratios of Multiple and Sub Multiple Angles

Chapter 10: Sine and Cosine Formulae and their Applications

Chapter 11: Trigonometric Equations

Chapter 12: Mathematical Induction

Chapter 13: Complex Numbers

Chapter 15: Linear Inequations

Chapter 16: Permutations

Chapter 17: Combinations

Chapter 18: Binomial Theorem

Chapter 19: Arithmetic Progressions

Chapter 20: Geometric Progressions

Chapter 21: Some Special Series

Chapter 22: Brief Review of Cartesian System of Rectangular Coordinates

Chapter 23: The Straight Lines

Chapter 24: The Circle

Chapter 25: Parabola

Chapter 26: Ellipse

Chapter 27: Hyperbola

Chapter 28: Introduction to 3D Coordinate Geometry

Chapter 29: Limits

Chapter 30: Derivatives

Chapter 31: Mathematical Reasoning

Chapter 32: Statistics

Chapter 33: Probability

Class 11 RD Sharma Solutions – Chapter 32 Statistics – Exercise 32.7

Question 1. Two plants A and B of a factory show the following results about the number of workers and the wages paid to them

Question 2. The means and standard deviations of heights and weights of 50 students in a class are as follows:

Question 3. The coefficient of variation of two distribution are 60% and 70%, and their standard deviations are 21 and 16 respectively. What is their arithmetic means?

Question 4. Calculate coefficient of variation from the following data:

Question 5. An analysis of the weekly wages paid to workers in two firms A and B, belonging to the same industry gives the following results:

Question 6. The following are some particulars of the distribution of weights of boys and girls in a class:

Question 7. The mean and standard deviation of marks obtained by 50 students of a class in three subjects, mathematics, physics and chemistry are given below:

Question 8. From the data given below state which group is more variable, G1 or G2?

Question 9. Find the coefficient of variation for the following data:

Question 10. From the prices of shares X and Y given below: find out which is more stable in value:

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?

Question 8. From the data given below state which group is more variable, G₁ or G₂?