Class 11 RD Sharma Solutions – Chapter 32 Statistics – Exercise 32.4
Last Updated :
21 Feb, 2021
Question 1. Find the mean, variance and standard deviation for the following data:
(i) 2, 4, 5, 6, 8, 17
(ii) 6, 7, 10, 12, 13, 4, 8, 12
(iii) 227, 235, 255, 269, 292, 299, 312, 321, 333, 348
(iv) 15, 22, 27, 11, 9, 21, 14,9
Solution:
(i)
| x | d = (x – Mean) | d2 |
| 2 | -5 | 25 |
| 4 | -3 | 9 |
| 5 | -2 | 4 |
| 6 | -1 | 1 |
| 8 | 1 | 1 |
| 17 | 10 | 100 |
| Total = 42 | | Total = 140 |
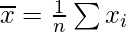
= 1/6[42] = 7
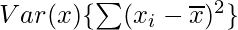
= 1/6[140] = 23.33
Standard deviation = √Var(x) = √23.33 = 4.8
(ii)
| x | d = (x – Mean) | d2 |
| 6 | -3 | 9 |
| 7 | -2 | 4 |
| 10 | 1 | 1 |
| 12 | 3 | 9 |
| 13 | 4 | 16 |
| 4 | -5 | 25 |
| 8 | -1 | 1 |
| 12 | 3 | 9 |
| Total = 72 | | Total = 74 |
Mean = 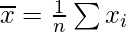
= 1/8[72] = 9
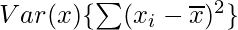
= 1/8[74] = 9.25
Standard deviation = √Var(x) = √9.25 = 3.04
(iii)
xi
| di = xi – 299
| di2
|
227
| -72
| 5184
|
235
| -64
| 4096
|
255
| -44
| 1936
|
269
| -30
| 900
|
292
| -7
| 49
|
299
| 0
| 0
|
312
| 13
| 169
|
321
| 22
| 484
|
333
| 34
| 1156
|
348
| 49
| 2401
|
| Total = -99
| Total = 16375
|
Mean =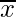 = 299 + (-99/10) = 289.1
= 299 + (-99/10) = 289.1
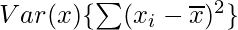
= 16375/10 – (-99/10)2
= 1637.5 – 98.01
= 1539.49
Standard deviation = √Var(x) = √1539.49 = 39.24
(iv)
| xi | di = xi – 15 | di2 |
15
| 0
| 0
|
22
| 7
| 49
|
27
| 12
| 144
|
11
| -4
| 16
|
9
| -6
| 36
|
21
| 6
| 36
|
14
| -1
| 1
|
9
| -6
| 36
|
| Total = 8
| Total = 318
|
Mean =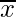 = 15 + 8/8 = 16
= 15 + 8/8 = 16
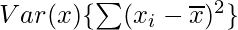
= 318/8 – 1 = 38.75
Standard deviation = √Var(x) = √38.75 = 6.22
Question 2. The variance of 20 observations is 4. If each observation is multiplied by 2, find the variance of the resulting observations.
Solution:
Given: n = 20, and 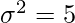
Now multiply each observation by 2, we get
Suppose X = 2x be the new data.
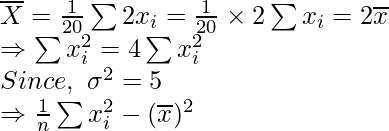 =5
=5
So, for the new data, we have
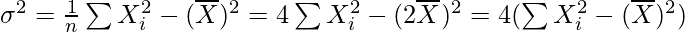
= 4 × 5
= 20
Question 3. The variance of 15 observations is 4. If each observation is increased by 9, find the variance of the resulting observations.
Solution:
Given: n = 15, and 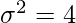
Now increase each observation by 9, we get
Suppose X = x + 9 be the new data.
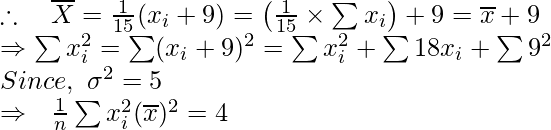
So for the new data:
![Rendered by QuickLaTeX.com \sigma^2=\frac{1}{n}\sum X_i^2-(\overline{X})^2=\frac{1}{15}(\sum x_i^2+\sum18x_i+\sum9^2)-(\overline{x}+9)^2\\ =\frac{1}{15}\sum x_i^2+15\sum18x_i+\frac{1}{15}\sum9^2-(9)^2-(18\overline{x})-(\overline{x})^2\\ =\left[\frac{1}{15}\sum x_i-(\overline{x})^2\right]+\left[\frac{1}{15}\sum18x_i-(18\overline{x})\right]+\left[\frac{1}{15}\sum9^2-(9)^2\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2461298b4fff891d8300b5cb4a211e0_l3.png)
![Rendered by QuickLaTeX.com =\left[\frac{1}{15}\sum x_i^2-(\overline{x})^2\right]+\left[18\times\frac{1}{15}\sum x_i-(18\overline{x})\right]+\left[\frac{1}{15}\times15\times(9)^2-(9)^2\right]\\ \frac{1}{15}\sum x_i^2-(\overline{x})^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3f0686bf95c912a235c48120bea74338_l3.png)
= 4
Question 4. The mean of 5 observations is 4.4 and their variance is 8.24. If three of the observations are 1, 2, and 6, find the other two observations.
Solution:
Let us considered the other two observations are x and y
Given: The mean of 5 observations is 4.4 and their variance is 8.24
So,
Mean = 1 + 2 + 6 + x + y = 5 × 4.4
= x + y = 13
Variance = [(1 – 4.4)2 + (2 – 4.4)2 + (6 – 4.4)2 + (x – 4.4)2 + (y – 4.4)3]
11.56 + 5.76 + 2.56 + (x – 4.4)2 + (y – 4.4)2 = 41.2
(x – 4.4)2 + (y – 4.4)2 = 21.32
On solving this equation, we get
(x – 4.4)2 + (13 – x – 4.4)2 = 21.32
(x – 4.4)2 + (8.6 – x)2 = 21.32
x2 – 8.8x + 19.36 + 73.96 – 17.2x + x2 = 21.32
2x2 – 26x + 72 = 0
x2 – 13x + 36 = 0
(x – 4)(x – 9) = 0
x = 4 or x = 9
So, the other two observation are 4 and 9.
Question 5. The mean and standard deviation of 6 observations are 8 and 4 respectively. If each observation is multiplied by 3, find the new mean and new standard deviation of the resulting observations.
Solution:
Given: Mean of 6 observations = 8
Standard Deviation of 6 observation = 4
k = 3
So, let us considered mean and Standard Deviation of the observation are 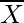 and
and 
then the mean and Standard Deviation of the observation multiplied by a constant ‘k’ are
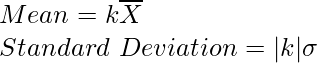
So, the new mean = 8 × 3 = 24
New Standard Deviation = 4 × 3 = 12
Question 6. The mean and variance of 8 observations are 9 and 9.25 respectively. If six of the observations are 6, 7, 10, 12, 12, and 13, find the remaining two observations.
Solution:
Given: Mean of 8 observations = 9
Standard Deviation of 8 observations = 9.25
Observations = 6, 7, 10, 12, 12, and 13
So, let us considered the other two observations are x and y
Mean = (6 + 7 + 10 + 12 + 12 + 13 + x + y)/8 = 9
= 60 + x + y =72
= x + y = 12 -(1)
Variance = 1/8(62 + 72 + 102 + 122 + 122 + 132 + x2 + y2) – (81)2 = 9.25
= 642 + x2 + y2 = 722
= x2 + y2 = 80 -(2)
Now, (x + y)2 + (x – y)2 = 2(x2 + y2)
= 144 + (x – y)2 = 2 × 80
= (x – y)2 = 16
= x – y = ±4
If x – y = 4, then x + y = 12 and x – y = 4
So, x = 8, y = 4
If x – y = -4 then x + y = 12 and x – y = -4
So, x = 4, y = 8
Hence, the remaining two observations are 4 and 8.
Question 7. For a group of 200 candidates, the mean and standard deviations of scores were found to be 40 and 15 respectively. Later on it was discovered that the scores of 43 and 35 were misread as 34 and 53 respectively. Find the correct mean and standard deviation.
Solution:
Given: n = 200, 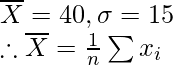
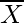 = 200 × 40 = 8000
= 200 × 40 = 8000
Corrected 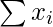 = Incorrect
= Incorrect 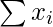 – (sum of incorrect values) + (sum of correct values)
– (sum of incorrect values) + (sum of correct values)
= 8000 – 34 – 53 + 43 + 35 = 7991
Corrected mean = 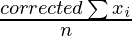
= 7991/200 = 39.955
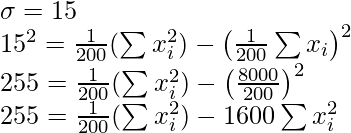
= 200 × 1825 = 365000
Incorrect 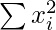 = 36500
= 36500
Corrected 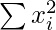 = (incorrect
= (incorrect 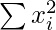 ) – (sum of squares of incorrect value) +
) – (sum of squares of incorrect value) +
(sum of squares of correct values)
= 365000 – (34)2 – 532 + (43)2 + 352 = 364109
So, Corrected 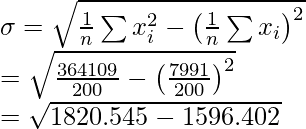
= 14.97
Question 8. The mean and standard deviation of 100 observations were calculated as 40 and 5.1 respectively by a student who took by mistake 50 instead of 40 for one observation. What are the correct mean and standard deviation?
Solution:
Given: n = 100, 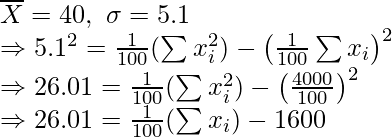
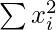 = 100 × 1626.01 = 162601
= 100 × 1626.01 = 162601
Incorrect = 162601
Corrected = (incorrect ) – (sum of squares of incorrect values) + (sum of squares of correct values)
= 162601 – (50)2 + (40)2 = 161701
So, Corrected 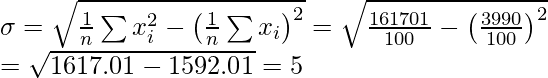
Question 9. The mean and standard deviation of 20 observations are found to be 10 and 2 respectively. On rechecking it was found that an observation 8 was incorrect. Calculate the correct mean and standard deviation in each of the following cases:
(i) If wrong item is omitted.
(ii) If it is replaced by 12.
Solution:
Given: n = 20, 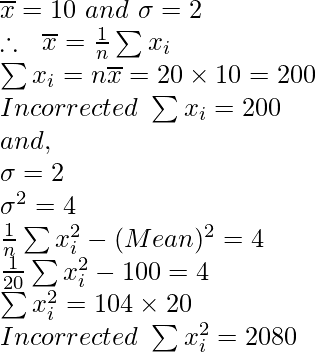
(i) If we remove 8 from the given observation then 19 observation are left.
Now, Incorrect 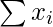 = 200
= 200
⇒ Corrected 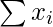 + 8 = 200
+ 8 = 200
⇒ Corrected 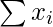 = 192
= 192
and,
⇒ Incorrect 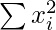 = 2080
= 2080
⇒ Corrected 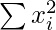 + 82 = 2080
+ 82 = 2080
⇒ Corrected 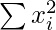 = 2080 – 64
= 2080 – 64
⇒ Corrected 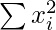 = 2016
= 2016
Therefore,
Corrected mean = 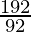 = 10.10
= 10.10
⇒ So, corrected variance = 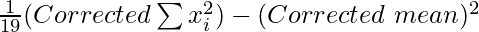
= 2016/19 – (192/19)2
= (38304 -36864)/361
= 1440/361
So, the corrected standard deviation = 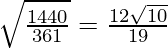 = 1.997
= 1.997
(ii) If we replace the incorrect observation(i.e., 8) by 12
Given: Incorrect 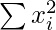 = 200
= 200
Therefore, Corrected 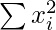 = 200 – 8 + 12 = 204
= 200 – 8 + 12 = 204
Incorrect 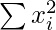 = 2080
= 2080
Therefore, Corrected 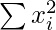 = 2080 – 82 + 122 = 2160
= 2080 – 82 + 122 = 2160
Now, Corrected mean = 204/20 = 10.2
Corrected variance = 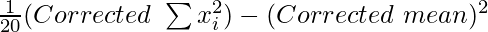
= 2016/20 – (204/20)2
= 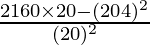
= 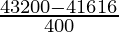
= 1584/400
So, the corrected standard deviation = 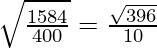
= 19.899/10 = 1.9899
Question 10. The mean and standard deviation of group of 100 observations were found to be 20 and 3 respectively. Later on it was found that three observations were incorrect, which were recorded as 21, 21, and 18. Find the mean and standard deviation if the incorrect observation were omitted.
Solution:
(i) Given: n = 100, 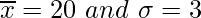
Mean = 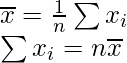
= 20 × 100 = 2000
Incorrect 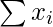 = 2000
= 2000
and,
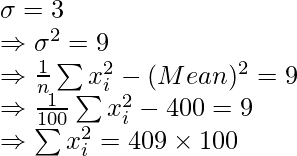
Incorrect 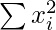 = 40900.
= 40900.
When the incorrect observations 21, 21, 18 are removed from the data
then the total number of observation are n = 97
Now,
Incorrect 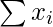 = 2000
= 2000
Corrected 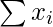 = 2000 – 21 – 21 – 18 = 1940
= 2000 – 21 – 21 – 18 = 1940
and,
Incorrect 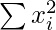 = 40900
= 40900
Corrected 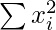 = 40900 – 212 – 212 – 182
= 40900 – 212 – 212 – 182
= 40900 – 1206
= 39694
Therefore, Corrected mean = 1940/97 = 20
Corrected variance = 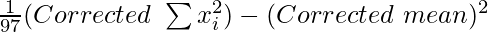
= (39694/97) – (20)2 = 409.22 – 400 = 9.22
So, the corrected standard deviation = √9.22 = 3.04
Question 11. Show that the two formulae for the standard deviation of ungrouped data
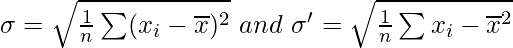
are equivalent, where 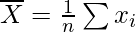
Solution:
Given:
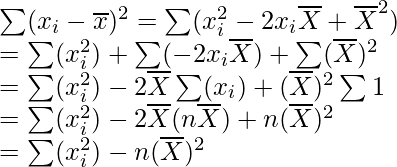
On dividing both the sides by n we get,
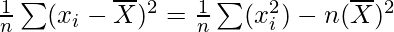
Now, taking square root on both the sides, we get
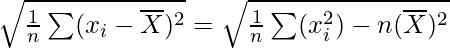
Share your thoughts in the comments
Please Login to comment...