RD Sharma Class 11 Solutions for Maths

Class 11 RD Sharma Solutions – Chapter 29 Limits – Exercise 29.6 | Set 1

Read

Discuss

Question 1. Lim_x→∞{(3x – 1)(4x – 2)}/{(x + 8)(x – 1)}.

Solution:

We have,

Lim_x→∞{(3x – 1)(4x – 2)}/{(x + 8)(x – 1)}

= $\lim_{x\to ∞}\frac{x(3-\frac{1}{x})x(4-\frac{2}{x})}{x(1+\frac{8}{x})x(1-\frac{1}{x})}$

= $\lim_{x\to∞}\frac{(3-\frac{1}{x})(4-\frac{2}{x})}{(1+\frac{8}{x})(1-\frac{1}{x})}$

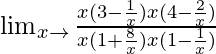
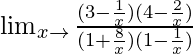
When x → ∞, (1/x) → 0.

= (3 × 4)/(1 × 1)

= 12

Question 2. Lim_x→∞{(3x³– 4x²+ 6x – 1)}/{(2x³+ x²– 5x + 7)}.

Solution:

We have,

Lim_x→∞{(3x³– 4x²+ 6x – 1)}/{(2x³+ x²– 5x + 7)}

= $\lim_{x\to∞}\frac{x^3(3-\frac{4}{x}+\frac{6}{x^2}-\frac{1}{x^3})}{x^3(2+\frac{1}{x}-\frac{5}{x^2}+\frac{7}{x^3})}$

= $\lim_{x\to∞}\frac{(3-\frac{4}{x}+\frac{6}{x^2}-\frac{1}{x^3})}{(2+\frac{1}{x}-\frac{5}{x^2}+\frac{7}{x^3})}$

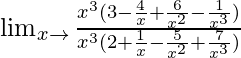
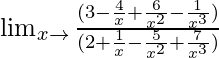
When x → ∞, (1/x), (1/x²), (1/x³) → 0.

= 3/2

Question 3. Lim_x→∞{(5x³– 6)}/{√(9 + 4x⁶)}.

Solution:

We have,

Lim_x→∞{(5x³– 6)}/{√(9 + 4x⁶)}

= $\lim_{x\to∞}\frac{x^3(5-\frac{6}{x^3})}{x^3\sqrt{(4+\frac{9}{x^6}})}$

= $\lim_{x\to∞}\frac{(5-\frac{6}{x^3})}{\sqrt{(4+\frac{9}{x^6}})}$

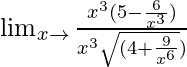
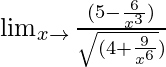
When x → ∞, (1/x), (1/x³) → 0.

= 5/√4

= 5/2

Question 4. Lim_x→∞{√(x²+ cx) – x}

Solution:

We have,

Lim_x→∞{√(x²+cx)-x}

On rationalizing numerator, we get

= Lim_x→∞{(x²+ cx) – x²}/{√(x²+ cx) + x}

= Lim_x→∞(cx)/{√(x²+ cx) + x}

= Lim_x→∞(cx)/[x{√(x + c/x) + 1}]

= Lim_x→∞(c)/{√(1 + c/x) + 1}

When x → ∞, (1/x) → 0.

= c/(√1 + 1)

= c/2

Question 5. Lim_x→∞{√(x + 1) – √x}

Solution:

We have,

Lim_x→∞{√(x + 1) – √x}

On rationalizing numerator, we get

= Lim_x→∞{(x+1)-x}/{√(x+1)+√x}

= Lim_x→∞(1)/{√(x+1)+√x}

= $\lim_{x\to∞}\frac{1}{\sqrt{x}(1+\frac{1}{x}+1)}$

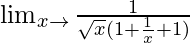
When x → ∞, (1/x) → 0.

= 0

Question 6. Lim_x→∞{√(x²+ 7x) – x}

Solution:

We have,

Lim_x→∞{√(x²+ 7x) – x}

On rationalizing numerator, we get

= Lim_x→∞{(x²+7x)-x2}/{√(x²+7x)+x}

= Limx→∞(7x)/{√(x²+7x)+x}

= $\lim_{x\to∞}\frac{7x}{x[\sqrt{(1+\frac{7}{x}})+1]}$

= $\lim_{x\to∞}\frac{7}{[\sqrt{(1+\frac{7}{x}})+1]}$

When x → ∞, (1/x) → 0.

= 7/(√1 + 1)

= 7/2

Question 7. Lim_x→∞(x)/{√(4x²+ 1) – 1}

Solution:

We have,

Lim_x→∞(x)/{√(4x²+ 1) – 1}

Rationalising denominator.

= Lim_x→∞[x{√(4x²+ 1) + 1}]/{(4x²+ 1) – 1}

= Lim_x→∞[x{√(4x²+ 1) + 1}]/(4x²)

= Lim_x→∞[{√(4x²+ 1) + 1}]/(4x)

= $\lim_{x\to∞}\frac{\sqrt{4+\frac{1}{x^2}}}{4}$

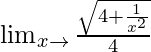
When x → ∞, (1/x²) → 0.

= √4/4

= 2/4

= 1/2

Question 8. Lim_n→∞(n²)/{1 + 2 + 3 + 4 + ……………. + n}

Solution:

We have,

Lim_n→∞(n²)/{1 + 2 + 3 + 4 + ……………. + n}

= $\lim_{n\to∞}\frac{n^2}{\frac{n(n+1)}{2}}$

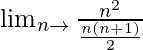
= Lim_n→∞(2n)/(n+1)

= Lim_n→∞(2)/(1+1/n)

When n → ∞, (1/n) → 0

= 2/(1 + 0)

= 2

Question 9. Lim_x→∞(3x^-1+ 4x^-2)/(5x^-1+ 6x^-2)

Solution:

We have,

Lim_x→∞(3x^-1+ 4x^-2)/(5x^-1+ 6x^-2)

= $\lim_{x\to∞}\frac{\frac{3}{x}+\frac{4}{x^2}}{\frac{5}{x}+\frac{6}{x^2}}$

= $\lim_{x\to∞}\frac{\frac{1}{x}(3+\frac{4}{x})}{\frac{1}{x}(5+\frac{6}{x})}$

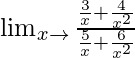
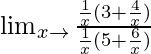
When x → ∞, (1/x) → 0.

= 3/5

Question 10. Lim_x→∞{√(x²+ a²) – √(x²+ b²)}/{√(x²+ c²) – √(x²+ d²)}

Solution:

We have,

Lim_x→∞{√(x²+ a²) – √(x²+ b²)}/{√(x²+ c²) – √(x²+ d²)}

On rationalizing numerator and denominator, we get

= $\lim_{x\to∞}\frac{(\sqrt{x^2+a^2}-\sqrt{x^2+b^2})(\sqrt{x^2+a^2}+\sqrt{x^2+b^2})(\sqrt{x^2+c^2}+\sqrt{x^2+d^2})}{(\sqrt{x^2+c^2}-\sqrt{x^2+d^2})(\sqrt{x^2+c^2}+\sqrt{x^2+d^2})(\sqrt{x^2+a^2}+\sqrt{x^2+b^2})}$

= $\lim_{x\to∞}\frac{(x^2+a^2)-(x^2+b^2))(\sqrt{x^2+c^2}+\sqrt{x^2+d^2})}{(x^2+c^2)-(x^2+d^2)(\sqrt{x^2+a^2}+\sqrt{x^2+b^2})}$

= $=\lim_{x\to∞}\frac{(a^2-b^2)(\sqrt{x^2+c^2}+\sqrt{x^2+d^2})}{(c^2-d^2)(\sqrt{x^2+a^2}+\sqrt{x^2+b^2})}$

= $\lim_{x\to∞}\frac{(a^2-b^2)\frac{1}{x}(\sqrt{(1+\frac{c^2}{x^2}})+\sqrt{(1+\frac{d^2}{x^2}}}{(c^2-d^2)\frac{1}{x}(\sqrt{1+\frac{a^2}{x^2}}+\sqrt{1+\frac{b^2}{x^2}})}$

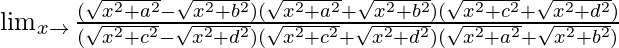
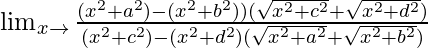
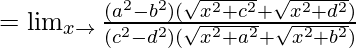
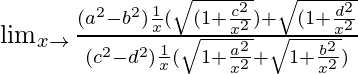
When x → ∞, (1/x²) → 0.

= $\frac{a^2-b^2}{c^2-d^2}×\frac{\sqrt{1}+\sqrt{1}}{\sqrt{1}+\sqrt{1}}$

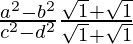
= (a²– b²)/(c²– d²)

Question 11. Lim_n→∞{(n + 2)! + (n + 1)!}/{(n + 2)! – (n + 1)!}.

Solution:

We have,

Lim_n→∞{(n + 2)! + (n + 1)!}/{(n + 2)! – (n + 1)!}

= Lim_n→∞{(n + 2)(n + 1)! + (n + 1)!}/{(n + 2)(n + 1)! – (n + 1)!}

= Lim_n→∞[(n + 1)!{(n + 2) + 1}]/[(n + 1)!{(n + 2) – 1}]

= Lim_n→∞(n + 3)/(n + 1)

= Lim_n→∞[n(1 + 3/n)]/[n(1 + 1/n)]

When n → ∞, (1/n) → 0.

= 1/1

= 1

Question 12. Lim_x→∞[x{√(x²+ 1) – √(x²– 1)}]

Solution:

We have,

Lim_x→∞[x{√(x²+ 1) – √(x²– 1)}]

On rationalizing numerator, we get

= Lim_x→∞[x{(x²+ 1) – (x²– 1)}]/{√(x²+ 1) + √(x²– 1)}

= Lim_x→∞(2x)/{√(x²+ 1) + √(x²– 1)}

= Lim_x→∞(2x)/[x{√(1 + 1/x²) + √(1 – 1/x²)}]

= Lim_x→∞(2)/[{√(1 + 1/x²) + √(1 – 1/x²)}]

When x → ∞, (1/x²) → 0.

= 2/(√1 + √1)

= 2/2

= 1

Question 13. Lim_x→∞[√(x + 2){√(x + 1) – √x}]

Solution:

We have,

Lim_x→∞[√(x + 2){√(x + 1) – √x}]

On rationalizing numerator, we get

= Lim_x→∞[√(x + 2){(x + 1) – x}]/{√(x + 1) + √x}

= Lim_x→∞[√(x + 2)]/{√(x + 1) + √x}

= Lim_x→∞[x√(1 + 2/x)]/[x{√(1 + 1/x) + √1}]

= Lim_x→∞[√(1 + 2/x)]/{√(1 + 1/x) + √1}

When x → ∞, (1/x) → 0.

= 1/(√1 + √1)

= 1/2

Last Updated : 30 Apr, 2021

Chapter 1: Sets

Chapter 2: Relations

Chapter 3: Functions

Chapter 4: Measurement of Angles

Chapter 5: Trigonometric Functions

Chapter 6: Graphs of Trigonometric Functions

Chapter 7: Trigonometric Ratios of Compound Angles

Chapter 8: Transformation Formulae

Chapter 9: Trigonometric Ratios of Multiple and Sub Multiple Angles

Chapter 10: Sine and Cosine Formulae and their Applications

Chapter 11: Trigonometric Equations

Chapter 12: Mathematical Induction

Chapter 13: Complex Numbers

Chapter 15: Linear Inequations

Chapter 16: Permutations

Chapter 17: Combinations

Chapter 18: Binomial Theorem

Chapter 19: Arithmetic Progressions

Chapter 20: Geometric Progressions

Chapter 21: Some Special Series

Chapter 22: Brief Review of Cartesian System of Rectangular Coordinates

Chapter 23: The Straight Lines

Chapter 24: The Circle

Chapter 25: Parabola

Chapter 26: Ellipse

Chapter 27: Hyperbola

Chapter 28: Introduction to 3D Coordinate Geometry

Chapter 29: Limits

Chapter 30: Derivatives

Chapter 31: Mathematical Reasoning

Chapter 32: Statistics

Chapter 33: Probability

Chapter 1: Sets

Chapter 2: Relations

Chapter 3: Functions

Chapter 4: Measurement of Angles

Chapter 5: Trigonometric Functions

Chapter 6: Graphs of Trigonometric Functions

Chapter 7: Trigonometric Ratios of Compound Angles

Chapter 8: Transformation Formulae

Chapter 9: Trigonometric Ratios of Multiple and Sub Multiple Angles

Chapter 10: Sine and Cosine Formulae and their Applications

Chapter 11: Trigonometric Equations

Chapter 12: Mathematical Induction

Chapter 13: Complex Numbers

Chapter 15: Linear Inequations

Chapter 16: Permutations

Chapter 17: Combinations

Chapter 18: Binomial Theorem

Chapter 19: Arithmetic Progressions

Chapter 20: Geometric Progressions

Chapter 21: Some Special Series

Chapter 22: Brief Review of Cartesian System of Rectangular Coordinates

Chapter 23: The Straight Lines

Chapter 24: The Circle

Chapter 25: Parabola

Chapter 26: Ellipse

Chapter 27: Hyperbola

Chapter 28: Introduction to 3D Coordinate Geometry

Chapter 29: Limits

Chapter 30: Derivatives

Chapter 31: Mathematical Reasoning

Chapter 32: Statistics

Chapter 33: Probability

Class 11 RD Sharma Solutions – Chapter 29 Limits – Exercise 29.6 | Set 1

Question 1. Limx→∞{(3x – 1)(4x – 2)}/{(x + 8)(x – 1)}.

Question 2. Limx→∞{(3x3 – 4x2 + 6x – 1)}/{(2x3 + x2 – 5x + 7)}.

Question 3. Limx→∞{(5x3 – 6)}/{√(9 + 4x6)}.

Question 4. Limx→∞{√(x2 + cx) – x}

Question 5. Limx→∞{√(x + 1) – √x}

Question 6. Limx→∞{√(x2 + 7x) – x}

Question 7. Limx→∞(x)/{√(4x2 + 1) – 1}

Question 8. Limn→∞(n2)/{1 + 2 + 3 + 4 + ……………. + n}

Question 9. Limx→∞(3x-1 + 4x-2)/(5x-1 + 6x-2)

Question 10. Limx→∞{√(x2 + a2) – √(x2 + b2)}/{√(x2 + c2) – √(x2 + d2)}

Question 11. Limn→∞{(n + 2)! + (n + 1)!}/{(n + 2)! – (n + 1)!}.

Question 12. Limx→∞[x{√(x2 + 1) – √(x2 – 1)}]

Question 13. Limx→∞[√(x + 2){√(x + 1) – √x}]

Please Login to comment...

Question 1. Lim_x→∞{(3x – 1)(4x – 2)}/{(x + 8)(x – 1)}.

Question 2. Lim_x→∞{(3x³– 4x²+ 6x – 1)}/{(2x³+ x²– 5x + 7)}.

Question 3. Lim_x→∞{(5x³– 6)}/{√(9 + 4x⁶)}.

Question 4. Lim_x→∞{√(x²+ cx) – x}

Question 5. Lim_x→∞{√(x + 1) – √x}

Question 6. Lim_x→∞{√(x²+ 7x) – x}

Question 7. Lim_x→∞(x)/{√(4x²+ 1) – 1}

Question 8. Lim_n→∞(n²)/{1 + 2 + 3 + 4 + ……………. + n}

Question 9. Lim_x→∞(3x^-1+ 4x^-2)/(5x^-1+ 6x^-2)

Question 10. Lim_x→∞{√(x²+ a²) – √(x²+ b²)}/{√(x²+ c²) – √(x²+ d²)}

Question 11. Lim_n→∞{(n + 2)! + (n + 1)!}/{(n + 2)! – (n + 1)!}.

Question 12. Lim_x→∞[x{√(x²+ 1) – √(x²– 1)}]

Question 13. Lim_x→∞[√(x + 2){√(x + 1) – √x}]