Class 11 RD Sharma Solutions – Chapter 29 Limits – Exercise 29.9
Last Updated :
07 Apr, 2021
Question 1. 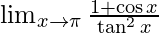
Solution:
Given,
By Applying limits, we get,
⇒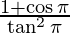 =
= 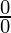 (Indeterminate form or 0/0 form)
(Indeterminate form or 0/0 form)
So, we cannot just directly apply the limits as we got indeterminate form.
On substituting  we get,
we get,
⇒ 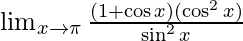
We know, sin2x + cos2x = 1
⇒ sin2x = 1 – cos2x
⇒ 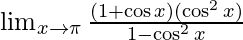
By using a2 − b2 = (a + b)(a − b) we get,
⇒ 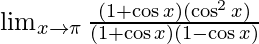
⇒ 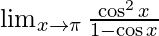
Applying limits we get,
⇒ 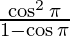
⇒ 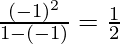
Therefore, the value of 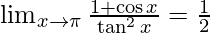
Question 2. 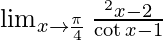
Solution:
Given,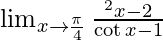
Applying the limits, we get,
⇒ 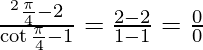 (Indeterminate form)
(Indeterminate form)
So, we cannot just directly apply the limits as we got indeterminate form.
We know, cosec2x − cot2x = 1
⇒ cosec2x = 1 + cot2x
⇒ 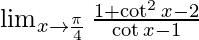
⇒ 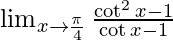
By using formula, a2 − b2 = (a + b)(a − b) we get,
⇒ 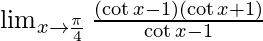
⇒ 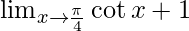
Applying the limits, we get,
⇒ 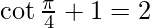
Therefore, the value of 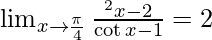
Question 3.
Solution:
Given,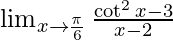
Applying the limits, we get,
⇒ 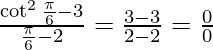 (Indeterminate form)
(Indeterminate form)
We know, cosec2x − cot2x = 1 ⇒ cot2x = cosec2x – 1
⇒ 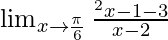
⇒ 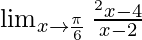
By using formula, a2 − b2 = (a + b)(a − b) we get,
⇒ 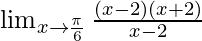
⇒ 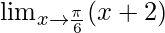
Applying the limits, we get,
⇒ 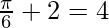
Therefore, the value of 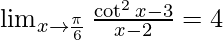
Question 4. 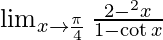
Solution:
Given,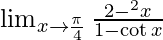
Applying the limits we get,
⇒  (Indeterminate form)
(Indeterminate form)
So, we cannot just apply the limits.
We know, cosec2x − cot2x = 1 ⇒ cosec2x = 1 – cot2x
⇒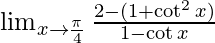
⇒ 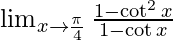
By using formula, a2 − b2 = (a + b)(a − b) we get,
⇒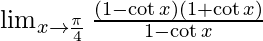
⇒ 
Applying the limits we get,
⇒ 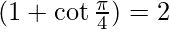
Therefore, The value of 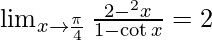
Question 5.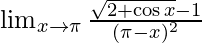
Solution:
Given,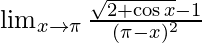
Applying the limits, we get,
⇒ 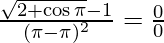 (Indeterminate form)
(Indeterminate form)
So, we cannot just apply the limits.
Rationalizing the numerator(multiplying and dividing with 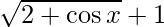 )
)
⇒ 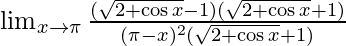
⇒ 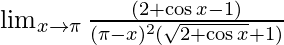
Let x = π − h
If x → π, h → 0
Substituting x = π − h we get,
⇒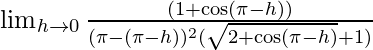
We know that cos(π − x) = −cosx substituting we get,
⇒ 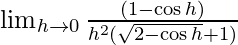
By using cos2x = 1 − 2sin2x ⇒ cos h = 1 − 2sin2(h/2)
⇒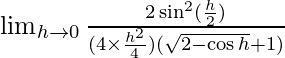
⇒ ![Rendered by QuickLaTeX.com \frac{1}{2} \lim_{h \to 0}[(\frac{\sin (\frac{h}{2})}{(\frac{h}{2})})^2\times(\frac{1}{\sqrt{2-\cos h}+1)})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fe2a47eb2b8e7f8b7dd848a3a1bc04ad_l3.png)
We know that, 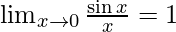
Applying the limits, we get,
⇒ 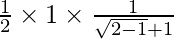
⇒ 1/2 x 1/2 = 1/4
Therefore, the value of 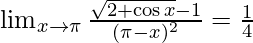
Question 6.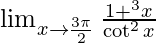
Solution:
Given,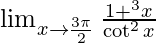
Applying the limits, we get,
⇒ 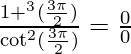 (Indeterminate form)
(Indeterminate form)
So, we cannot just directly apply the limits,
By using the formula, a3 + b3 = (a + b)(a2 − ab + b2) we get,
⇒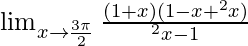
By using formula, a2 − b2 = (a + b)(a − b)
⇒ 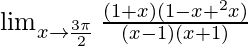
⇒ 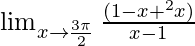
Applying the limits, we get,
⇒ 
Therefore, the value of 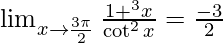
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...