Question 1: Find the equation of the straight lines passing through the origin and making an angle of 45° with the straight line √3x+y = 11.
Solution:
As line 1 passes through origin, there won’t be any intercept, and it will be in the form of y = mx (m as slope)
For line 2: √3x+y = 11, slope is M = -√3
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
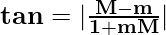
Here, we have θ = 45°, m=m and M = -√3
tan 45° = 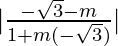
1 = 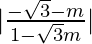
We will have two cases,
1 = 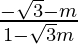 and 1 =
and 1 = 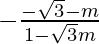
1-√3m = -√3-m and 1-√3m = √3+m
√3m-m = 1+√3 and √3m+m = 1-√3
m = 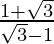 and m =
and m = 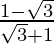
By rationalizing, we get
m = 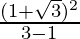 and m =
and m = 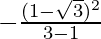
m = 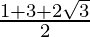 and m =
and m = 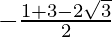
m = 2+√3 and m = -(2-√3)
m = √3+2 and m = √3-2
Hence, the equation of line will be,
y = (√3+2)x and y = (√3-2)x
Question 2: Find the equation to the straight lines which pass through the origin and are inclines at an angle of 75° to the straight line x+y+√3(y-x)=a.
Solution:
As line 1 passes through origin, there won’t be any intercept and it will be in the form of y = mx (m as slope)
For line 2: x+y+√3(y-x)=a,
x+y+√3y-√3x=a
x(1-√3)+y(1+√3)=a
slope is M = 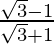
After rationalizing, we get
M = 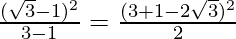 = 2-√3
= 2-√3
Here, it is given that these two lines make an angle of 75° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
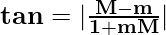
Here, we have θ = 75°, m=m and M = 2-√3
tan 75° = 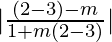
tan (45°+30°)= 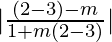
Using the trigonometric identity,
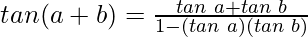
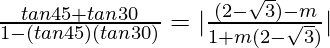
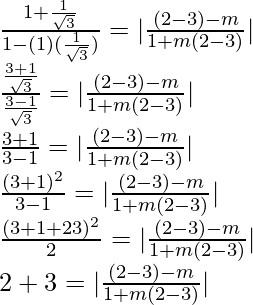
We will have two cases,
2+√3 = 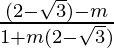 and 2+√3 =
and 2+√3 = 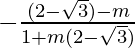
(2+√3)(1+m(2-√3)) = 2-√3-m and (2+√3)(1+m(2-√3)) = -(2-√3-m)
(2+√3+m(22-(√3)2) = 2-√3-m and (2+√3+m(22-(√3)2) = √3-2+m
2+√3+m(4-3) = 2-√3-m and 2+√3+m(4-3) = √3-2+m
2+√3+m+m = 2-√3 and 2+√3+m-m = √3-2
2m = -2-√3+2-√3 and 2+√3 = √3-2
2m = -2√3 and m is not defined
m = -√3 and m is not defined
Hence, the equation of line will be,
y = -√3x and x = 0
Question 3: Find the equation of the straight lines passing through (2,-1) and making an angle of 45° with the line 6x+5y-8=0.
Solution:
As line 1 passes through (2,-1), then it will be in the form of
y-(-1) = m(x-2) (m as slope)
y+1 = m(x-2)
For line 2: 6x+5y-8=0
5y = -6x + 8
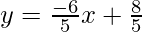
slope is M = 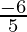
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
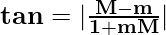
Here, we have θ = 45°, m=m and M = 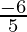
tan 45° = 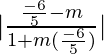
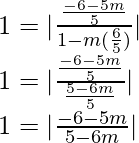
We will have two cases,
1 = 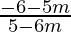 and 1 =
and 1 = 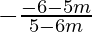
5-6m = -6-5m and 5-6m = -(-6-5m)
6m-5m = 5+6 and 5-6m = 5m+6
m = 11 and 5m+6m = 5-6
m = 11 and m = 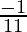
Hence, the equation of line will be,
y+1 = 11(x-2) and y+1 = 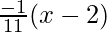
11x-y-23=0 and 11y+x+9 = 0
Question 4: Find the equation to the straight lines which pass through the point (h,k) and are inclined at angle tan-1 m to the straight line y=mx+c.
Solution:
As line 1 passes through (h,k), then it will be in the form of
y-(k) = M(x-h) (M as slope)
For line 2: y=mx+c (m as slope)
Here, it is given that these two lines make an angle of tan-1 m between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
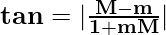
Here, we have θ = tan-1 m,
tan (tan-1 m) = 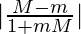
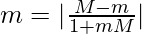
We will have two cases,
m = 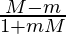 and m =
and m = 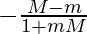
m(1+mM) = M-m and m(1+mM) = -(M-m)
m+m2M = M-m and m+m2M = m-M
2m = M-m2M and m2M = -M
M = 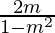 and M = 0
and M = 0
Hence, the equation of line will be,
y-(k) = 0(x-h) and y-k = 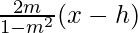
y-k = 0 and (y-k)(1-m2) = (2m)(x-h)
Question 5: Find the equation to the straight lines passing through the point (2,3) and inclined at 45° to the line 3x+y-5=0.
Solution:
As line 1 passes through (2,3), then it will be in the form of
y-3 = M(x-2) (M as slope)
For line 2: 3x+y-5=0
y = -3x+5
slope m = -3
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
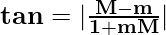
Here, we have θ = 45°,
tan 45° = 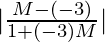
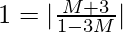
We will have two cases,
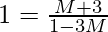 and
and 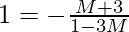
1-3M = M+3 and 1-3M = -(M+3)
M+3M = 1-3 and 1-3M = -M-3
4M = -2 and 3M-M = 1+3
M = 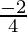 and 2M = 4
and 2M = 4
M = 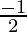 and M = 2
and M = 2
Hence, the equation of line will be,
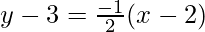 and y-3 = 2(x-2)
and y-3 = 2(x-2)
2y-6 = -(x-2) and y-3 = 2x-4
x+2y-8=0 and 2x-y-1=0
Question 6: Find the equation to the sides of an isosceles right-angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2,2).
Solution:
As △ABC is an isosceles right angled triangle at B.
∠A = ∠C = 45°
We can say that, AB and BC makes 45° with AC.
Let the slope of AB as m1 and BC as m2.
AB: (y-2) = m1(x-2)
BC: (y-2) = m2(x-2)
Slope of AC : 3x+4y=4
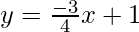
Slope of AC is 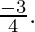

Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
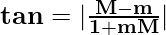
Here, we have θ = 45°, and M = 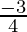
tan 45° = 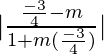
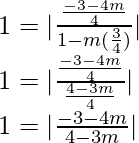
We will have two cases,
1 = 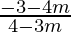 and 1 =
and 1 = 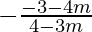
4-3 = -3-4 and 4-3 = -(-3-4)
4m-3 = -3-4 and 4-3 = 3+4
m = -7 and 4+3 = 4-3
m = -7 and m = 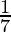
Hence, the equation of lines will be,
AB: (y-2) = m1(x-2)
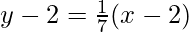
7y-x-12=0
BC: (y-2) = m2(x-2)
y-2 = -7(x-2)
7x+y-16=0
Question 7: The equation of one side of an equilateral triangle is x-y=0 and one vertex is (2+√3,5). Prove that a second side is y+(2-√3)x=6 and find the equation of the third side.
Solution:
As equation of one side of equilateral triangle is x-y=0 and one vertex is (2+√3,5),
As, the point (2+√3,5) does not satisfy x-y=0. Then this is the vertex opposite of the line x-y=0

In equilateral triangle,
∠A = ∠B = ∠C = 60°
We can say that, AC and BC makes 60° with AB.
Let the slope of AC as m1 and BC as m2.
AB: (y-5) = m1(x-(2+√3))
BC: (y-5) = m2(x-(2+√3))
Slope of AC : x-y=0
y = x
Slope of AC is 1.
Here, it is given that these two lines make an angle of 60° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
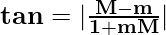
Here, we have θ = 60°, m = m1 and m2 and M = 1
tan 60° = 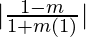
√3= 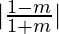
We will have two cases,
√3 = 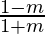 and √3 =
and √3 = 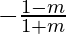
m = 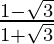 and √3(1+m) = -(1-m)
and √3(1+m) = -(1-m)
m = 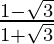 and √3+√3m = m-1
and √3+√3m = m-1
m = 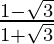 and √3m-m = -1-√3
and √3m-m = -1-√3
m = 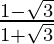 and m =
and m = 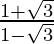
After rationalizing, we get
m = 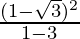 and m =
and m = 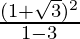
m = 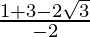 and m =
and m = 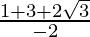
m = -(2-√3) and m = -(2+√3)
Hence, the equation of lines will be,
AB: (y-5) = m1(x-(2+√3))
y-5 = -(2-√3)(x-(2+√3))
y-5 = -(2-√3)x+ (22-(√3)2)
(2-√3)x+y-6 = 0
BC: (y-5) = m2(x-(2+√3))
(y-5) = -(2+√3)(x-(2+√3))
y-5 = -(2+√3)x+(2+√3)^2
(2+√3)x+y-5 = 4+3+4√3
(2+√3)x+y = 12+4√3
Question 8: Find the equation of the two straight lines passing through (1,2) forming two sides of a square of which 4x+7y=12 is one diagonal.
Solution:
Let the point opposite of diagonal 4x+7y=12 be C(1,2)
Here, △BCD form an isosceles right angled triangle at C.
∠B = ∠D = 45°
We can say that, CD and BC makes 45° with BD.

Let the slope of CD as m1 and BC as m2.
CD: (y-2) = m1(x-1)
BC: (y-2) = m2(x-1)
Slope of BD : 4x+7y=12
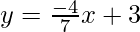
Slope of BD is 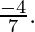
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
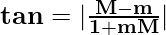
Here, we have θ = 45° and M = 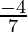
tan 45° = 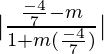
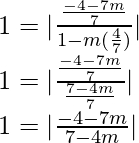
We will have two cases,
1 = 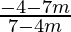 and 1 =
and 1 = 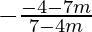
7-4m = -4-7m and 7-4m = -(-4-7m)
7m-4m = -4-7 and 7-4m = 4+7m
3m = -11 and 7m+4m = 7-4
m = 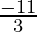 and 11m = 3
and 11m = 3
m = 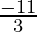 and m =
and m = 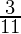
Hence, the equation of lines will be,
CD: (y-2) = m1(x-1)
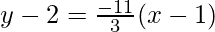
3y-6 = -11x+11
11x+3y-17=0
BC: (y-2) = m2(x-1)
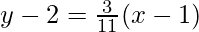
11y-22 = 3x-3
3x-11y+19=0
Question 9: Find the equation of the two straight lines passing through (1,2) and making an angle of 60° with the line x+y=0. Find also the area of the triangle formed by the three lines.
Solution:
As equation of one side of equilateral triangle is x+y=0 and one vertex is (1,2),
As, the point (1,2) does not satisfy x+y=0. Then this is the vertex opposite of the line x+y=0
Hence, the lines make an equilateral triangle,
∠A = ∠B = ∠C = 60°
We can say that, AC and BC makes 60° with AB.

Let the slope of AC as m1 and BC as m2.
AB: (y-2) = m1(x-1)
BC: (y-2) = m2(x-1)
Slope of AC : x+y=0
y = -x
Slope of AC is -1.
Here, it is given that these two lines make an angle of 60° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
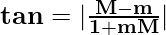
Here, we have θ = 60° and M = -1
tan 60° = 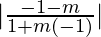
√3= 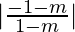
We will have two cases,
√3 = 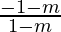 and √3 =
and √3 = 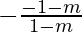
√3(1-m) = -1-m and √3(1-m) = 1+m
√3-√3m = -1-m and √3-√3m = m+1
√3m-m = √3+1 and +√3m+m = √3-1
m = 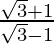 and m =
and m = 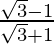
After rationalizing, we get
m = 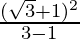 and m =
and m = 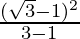
m = 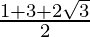 and m =
and m = 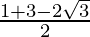
m = 2+√3 and m = 2-√3
Hence, the equation of lines will be,
AB: (y-2) = (2+√3)(x-1)
y-2=(2+√3)x-2-√3
(2+√3)x-y-√3=0 ……………….(i)
BC: (y-2) = (2-√3)(x-1)
y-2=(2-√3)x-2+√3
(2-√3)x-y+√3=0 ……………….(ii)
Using (i) and x+y=0, we get
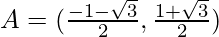
C = (1,2)
Using distance formula, AC
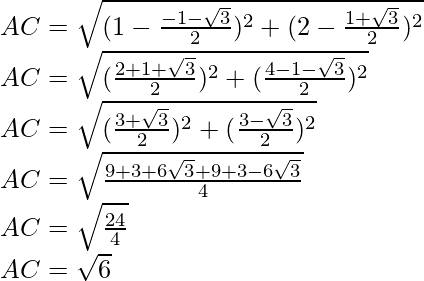
Area of equilateral triangle ABC,
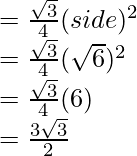 sq. unit
sq. unit
Question 10: Two sides of an isosceles triangle are given by the equations 7x-y+3=0 and x+y-3=0 and its third side passes through the point (1,-10). Determine the equation of the third side.
Solution:
Let the equation of the line AB and AC 7x-y+3=0 and x+y-3=0 respectively.
∠B = ∠C

Slope of line AB: 7x-y+3=0
y = 7x+3
Slope m1 = 7
Slope of line AC: x+y-3=0
y = -x+3
Slope m2 = -1
Let the slope of line BC be m, which passes through the point (1,-10)
y-(-10) = m(x-1)
y+10 = m(x-1)
The angle between the lines AB and BC is equal to the angle between the lines AC and BC, say θ
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
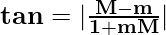
By taking positive sign
tan θ = 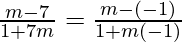
tan θ = 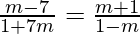
Solving it, we get
m = -3 or 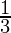
By taking negative sign
tan θ = 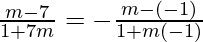
tan θ = 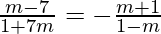
Solving it, we get
m2 = -1 (which is not possible)
Line BC: when m = -3
y+10 = -3(x-1)
y+10 = -3x+3
3x+y-13=0
Line BC: when m = 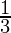
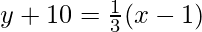
3y+30 = x-1
x-3y-31=0
Question 11: Show that the point (3,-5) lies between the parallel lines 2x+3y-7=0 and 2x+3y+12=0 and find the equation of lines through (3,-5) cutting the above lines at an angle of 45°.
Solution:
Let the line 1: 2x+3y-7=0
Line 2: 2x+3y+12=0
As the slope of line 1 and line 2 is same, these lines are parallel.
Slope of lines M = 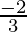
To check whether (3,-5) lies between these lines
Taking x=3 and y=-5
(2x+3y-7)(2x+3y+12)<0 (If its true then the point lies between these lines)
(2(3)+3(-5)-7)(2(3)+3(-5)+12)
(6-15-7)(6-15+12)
(-16)(3) <0, which is a negative value.
Hence, the point (3,-5) lies between the lines.

Let the slope of the line be m, which is passing through the point (3,-5)
y-(-5) = m(x-3)
y+5 = m(x-3)
As it is given that the line is cutting above lines at an angle of 45°.
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
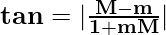
Taking θ = 45° and M = 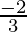
By taking positive sign
tan 45° = 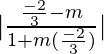
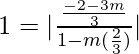
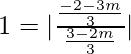
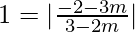
We will have two cases,
1 = 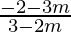 and 1 =
and 1 = 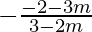
3-2m = -2-3m and 3-2m = -(-2-3m)
3m-2m = -2-3 and 3-2m = 2+3m
m = -5 and 3m+2m = 3-2
m = -5 and m = 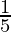
Hence, the equation of line will be,
when m = -5
y+5 = (-5)(x-3)
y+5 = -5x+15
5x+y-10=0
when m = 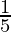
y+5 = 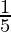 (x-3)
(x-3)
5y+25 = x-3
x-5y-28=0
Question 12: The equation of the base of an equilateral triangle is x+y=2 and its vertex is (2,-1). Find the length and equations of its sides.
Solution:
∠A = ∠B = ∠C = 60°
We can say that, AC and AB makes 60° with BC.

Let the slope of AC as m1 and AB as m2 which passes through the point (2,-1).
AB: (y-(-1)) = m1(x-2)
y+1 = m1(x-2)
AC: (y-(-1)) = m2(x-2)
y+1 = m2(x-2)
Slope of BC : x+y=2
y = -x+2
Slope of BC is -1.
Here, it is given that these two lines make an angle of 60° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
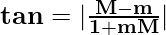
Here, we have θ = 60°, m = m1 and m2 and M = -1
tan 60° = 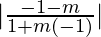
√3= 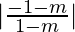
We will have two cases,
√3 = 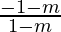 and √3 =
and √3 = 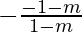
√3(1-m) = -1-m and √3(1-m) = 1+m
√3-√3m = -1-m and √3-√3m = m+1
√3m-m = √3+1 and +√3m+m = √3-1
m = 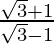 and m =
and m = 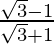
After rationalizing, we get
m = 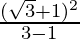 and m =
and m = 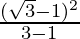
m = 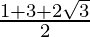 and m =
and m = 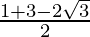
m = 2+√3 and m = 2-√3
Hence, the equation of lines will be,
AB: y+1 = m1(x-2)
y+1 = (2+√3)(x-2)
y+1 = (2+√3)x-4-2√3
(2+√3)x-y-5-2√3=0 ……………….(i)
AC: y+1 = m2(x-2)
y+1 = (2-√3)(x-2)
y+1 = (2-√3)x-4+2√3
(2-√3)x-y-5+2√3=0 ……………….(ii)
Using (ii) and x+y=2, we get
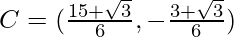
A = (2,-1)
Using distance formula, AC
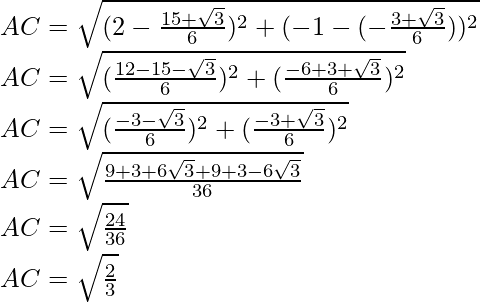
AC = AB = BC = 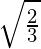
Question 13: If two opposite vertices of a square are (1,2) and (5,8), find the coordinates of its other two vertices and the equations of its sides.
Solution:
Let’s consider a square ABCD.
According to the property of square, the diagonal bisects the angle.
Hence, ∠AOB = ∠AOD = 45°

Slope of the diagonal AC:
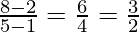
Let the slope of the line AB and AD be m1 and m2, which passes through the point (1,2)
AB: y-2 = m1(x-1)
AD: y-2 = m2(x-1)
Here, it is given that these two lines make an angle of 45° with AC. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
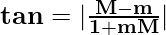
Here, we have θ = 45°, m = m1 and m2 and M = 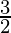
tan 45° = 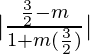
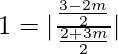
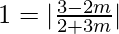
We will have two cases,
1 = 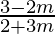 and 1 =
and 1 = 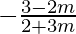
2+3m = 3-2m and 2+3m = -(3-2m)
3m+2m = 3-2 and 2+3m = 2m-3
5m = 1 and 3m-2m = -3-2
m = 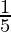 and m = -5
and m = -5
m = 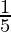 or -5
or -5
Hence, the equation of lines will be,
AB: y-2 = m1(x-1)
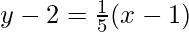
5y-10 = x-1
x-5y+9=0 ……………….(i)
AD: y-2 = m2(x-1)
y-2 = -5(x-1)
y-2 = -5x+5
5x+y-7=0 ……………….(ii)
As BC is parallel to AD, So
The equation BC will be 5x+y+λ=0 and as BC passes through C(5,8), we get
5(5)+(8)+λ=0
33+λ=0
λ = -33
Hence, Equation of BC is 5x+y-33=0 ……………….(iii)
Now as CD is parallel to AB, So
The equation CD will be x-5y+λ=0 and as CD passes through C(5,8), we get
5-5(8)+λ=0
-35+λ=0
λ = 35
Hence, Equation of CD is x-5y+35=0 ………………………(iv)
Solving (i) and (iii), we get
B(6,3)
Solving (ii) and (iv), we get
D(0,7)
Hence, the equation of lines are
AB = x-5y+9=0
BC = 5x+y-33=0
CD = x-5y+35=0
AD = 5x+y-7=0
And the vertices of square are
A(1,2), B(6,3), C(5,8) and D(6,3)
Share your thoughts in the comments
Please Login to comment...