Question 1. Find the sum of the following arithmetic progressions:
(i) 50, 46, 42, … to 10 terms
Solution:
Given A.P. has first term(a) = 50,
Common difference(d) = 46 – 50 = – 4
and number of terms(n) = 10
So, Sum of A.P. = S10 = n[2a + (n – 1)d] / 2
= 10[2(50) + (10 – 1)(-4)]/2
= (10)(100 – 36)/2
= 320
Hence, the sum of the first 10 terms of A.P. is 320.
(ii) 1, 3, 5, 7, …..to 12 terms.
Solution:
Given A.P. has first term(a) = 1,
common difference(d) = 3 – 1 = 2
and number of terms(n) = 12
So, Sum of A.P. = S12 = n[2a + (n – 1)d] / 2
= 12[2(1) + (12 – 1)(2)]/2
= 12[2 + 22]/2
= 144
Hence, the sum of the first 12 terms of A.P. is 144.
(iii) 3, 9/2, 6, 15/2, … to 25 terms
Solution:
Given A.P. has first term(a) = 3,
Common difference(d) = 9/2 – 3 = 3/2
and number of terms(n) = 25
So, Sum of A.P. = S25 = n[2a + (n – 1)d] / 2
= 25[2(3) + (25 – 1)(3/2)]/2
= 25[6 + 36]/2 = 525
Hence, the sum of the first 25 terms of A.P. is 525.
(iv) 41, 36, 31, ….. to 12 terms.
Solution:
Given A.P. has first term(a) = 41,
Common difference(d) = 36 – 41 = -5
and number of terms(n) = 12
So, Sum of A.P. = S12 = n[2a + (n – 1)d] / 2
= 12[2(41) + (12 – 1)(-5)]/2
= 12[82 – 55] = 162
Hence, the sum of the first 12 terms of A.P. is 162.
(v) a + b, a – b, a – 3b, ….. to 22 terms
Solution:
Given A.P. has first term(a) = a + b,
Common difference(d) = (a – b) – (a + b) = -2b
and number of terms(n) = 22
So, Sum of A.P. = S22 = n[2a + (n – 1)d] / 2
= 22[2(a + b) + (22 – 1)(-2b)]/2
= 11{2(a + b) – 22b)
= 11(2a – 40b) = 22a – 440b
Hence, the sum of the first 22 terms of A.P. is 22a – 440b.
(vi) (x – y)2,(x2 + y2), (x + y)2,… to n terms
Solution:
Given A.P. has first term(a) = (x – y)2,
number of terms(n) = n and
Common difference(d) = x2 + y2 – (x – y)2 = x2 + y2 – x2 + y2 + 2xy = 2xy
So, Sum of A.P. = Sn = n[2a + (n – 1)d] / 2
= n[2(x – y)2+(n – 1)(2xy)]/2
= n[(x – y)2+(n – 1)(xy)]
Hence, the sum of the first n terms of A.P. is n[(x – y)2+(n – 1)(xy)].
(vii) 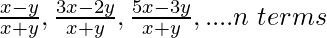
Solution:
Given A.P. has first term(a) = 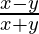
number of terms(n) = n and
Common difference(d) = 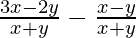
= 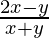
So, Sum of A.P. = Sn = n[2a + (n – 1)d] / 2
= ![Rendered by QuickLaTeX.com n\left[2\left(\frac{x-y}{x+y}\right) + (n-1) \left(\frac{2x-y}{x+y}\right)\right]/2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ee8b2d90e20a5c12f9501ebb80e1e974_l3.png)
= 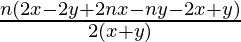
= ![Rendered by QuickLaTeX.com \frac{n[n(2x-y)]}{2(x+y)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10168270acf4ce592ec9668eaccf1248_l3.png)
Hence, the sum of the first n terms of A.P. is ![Rendered by QuickLaTeX.com \frac{n[n(2x-y)]}{2(x+y)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10168270acf4ce592ec9668eaccf1248_l3.png)
(viii) –26, –24, –22,…. to 36 terms
Solution:
Given A.P. has first term(a) = -26,
Common difference(d) = -24 – (-26) = 2
and number of terms(n) = n.
So, Sum of A.P. = S36 = n[2a + (n – 1)d] / 2
= 36[2(-26) + (36 – 1)2]/2
= 18[-52 + 70] = 324
Hence, the sum of the first 36 terms of A.P. is 324.
Question 2. Find the sum to n terms of the A.P. 5, 2, –1, – 4, –7, …
Solution:
Given A.P. has first term(a) = 5,
Common difference(d) = 2 – 5 = -3
Sum of n terms of A.P. = Sn = n[2a + (n – 1)d] / 2
= n[2(5) + (n – 1)(-3)] / 2
= n{10 – 3n + 3)} / 2
= n / 2(13 – 3n)
Hence, the sum of the n terms of A.P. is n/2(13 – 3n).
Question 3. Find the sum of n terms of an A.P. whose terms are given by an = 5 – 6n.
Solution:
Given A.P. has nth term, an = 5 – 6n
Putting n = 1, we get a, first term of the A.P.,
a = 5 – 6(1) = -1
Sum of n terms of A.P. = Sn = n[a + an]/2
= n[-1 + (5 – 6n)]/2
= n(4 – 6n)/2 = n(2 – 3n)
Hence, the sum of the n terms of A.P. is n(2 – 3n).
Question 4. Find the sum of the last ten terms of the A.P. : 8, 10, 12, 14, .. , 126.
Solution:
Given A.P. has first term(a) = 8,
Common difference(d) = 10 – 8 = 2
and nth term(an) = 126.
The nth term of the A.P. is given by, an = a+(n – 1)d
=> 126 = 8 + (n – 1)(2)
=> 126 = 8 + 2n – 2
=> 2n = 120
=> n = 60
We have to find the sum of last ten terms i.e.,
S = a51 + a52 + a53 + ……. + a60
a51 = 8 + (51 – 1)(2) = 8 + 50(2) = 108
So, sum would be S = 10[108 + 126]/2 = 5(234) = 1170
Hence, the sum of last 10 terms of the A.P. is 1170.
Question 5. Find the sum of first 15 terms of each of the following sequences having nth term as:
(i) an = 3 + 4n
Solution:
Given A.P. has nth term, an = 3 + 4n
and number of terms(n) = 15
So, an = 3 + 4(15) = 63
On putting n = 1, we get a, first term of the A.P.,
a = 3 + 4(1) = 7
S15 = n[a + an]/2
= 15(7 + 63)/2 = 15 x 35 = 525
Hence, the sum of the first 15 terms of given A.P. is 525.
(ii) bn = 5 + 2n
Solution:
Given A.P. has nth term, an = 5 + 2n and
number of terms(n) = 15
So, an = 5 + 2(15) = 35
On putting n = 1, we get a, first term of the A.P.,
a = 5 + 2(1) = 7
S15 = n[a + an]/2
= 15(7 + 35)/2 = 15 x 21 = 315
Hence, the sum of the first 15 terms of given A.P. is 315.
(iii) xn = 6 – n
Solution:
Given A.P. has nth term, an = 6 – n
and number of terms(n) = 15
So, an = 6 – n = -9
On putting n = 1, we get a, first term of the A.P.,
a = 6 – 1 = 5
S15 = n[a + an]/2
= 15(5 – 9)/2 = 15 x (-2) = -30
Hence, the sum of the first 15 terms of given A.P. is -30.
(iv) yn = 9 – 5n
Solution:
Given A.P. has nth term, an = 9 – 5n
and number of terms(n) = 15
So, an = 9 – 5(15) = -66
On putting n = 1, we get a, first term of the A.P.,
a = 9 – 5 = 4
S15 = n[a + an]/2
= 15(4 – 66)/2 = 15 x (-31) = -465
Hence, the sum of the first 15 terms of given A.P. is -465.
Question 6. Find the sum of first 20 terms the sequence whose nth term is an = An + B.
Solution:
Given A.P. has nth term, an = An + B
and number of terms(n) = 20
So, an = A(20) + B = 20A + B
On putting n = 1, we get a, first term of the A.P.,
a = A(1) + B = A + B
S20 = n[a + an]/2
= 20(A+B + 20A + B)/2
= 10[21A + 2B]
= 210A + 20B
Hence, the sum of the first 20 terms of given A.P. is 210A + 20B.
Question 7. Find the sum of first 25 terms of an A.P whose nth term is given by an = 2 – 3n.
Solution:
Given A.P. has nth term, an = 2 – 3n
and number of terms(n) = 25
So, an = 2 – 3(25) = -73
On putting n = 1, we get a, first term of the A.P.,
a = 2 – 3(1) = -1
S20 = n[a + an]/2
= 25(-1 – 73)/2
= 25 x (-37) = -925
Hence, the sum of the first 25 terms of given A.P. is -925.
Question 8. Find the sum of first 25 terms of an A.P whose nth term is given by an = 7 – 3n.
Solution:
Given A.P. has nth term, an = 7 – 3n
and number of terms(n) = 25
So, an = 7 – 3(25) = -68
On putting n = 1, we get a, first term of the A.P.,
a = 7 – 3(1) = 4
S25 = n[a + an]/2
= 25(4 – 68)/2
= 25 x (-32)
= -800
Hence, the sum of the first 25 terms of given A.P. is -800.
Question 9. If the sum of a certain number of terms starting from first term of an A.P. is 25, 22, 19, . . ., is 116. Find the last term.
Solution:
Given A.P. has first term(a) = 25,
Common difference(d) = 22 – 25 = -3 and sum(Sn) = 116.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n – 1)d] / 2.
=> 116 = n[2(25) + (n − 1)(−3)]/2
=> n[53 − 3n]/2 = 116
=> 53n – 3n2 = 232
=> 3n2 – 53n + 232 = 0
=> 3n2 – 24n – 29n + 232 = 0
=> 3n(n – 8) – 29 (n – 8) = 0
=> (3n – 29)( n – 8 ) = 0
=> n = 29/3 or n = 8
Ignoring n = 29/3 as number of terms cannot be a fraction, so we get, n = 8.
So, the last term is:
a8 = a + (8 – 1)d = 25 + 7(-3) = 25 – 21 = 4
Hence, the last term of the given A.P. is 4.
Question 10 (i). How many terms of the sequence 18, 16, 14…. should be taken so that their sum is zero.
Solution:
Given A.P. has first term(a) = 18,
Common difference(d) = 16 – 18 = -2 and sum(Sn) = 0.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n – 1)d] / 2.
=> 0 = n[2(18) + (n – 1)(-2)]/2
=> 0 = n[36 + (-2n + 2)]/2
=> n[38 − 2n] = 0
=> n = 0 or 38 – 2n = 0
Ignoring n = 0 as number of terms cannot be 0. So we get,
=> 38 – 2n = 0
=> 2n = 38
=> n = 19
Hence, the number of terms(n) is 19.
(ii) How many terms are there in the A.P. whose first and fifth terms are –14 and 2 respectively and the sum of the terms is 40?
Solution:
Given A.P. has first term(a) = –14,
Fifth term(a5) = 2 and sum(Sn) = 40.
Let the common difference of the A.P. be d. We get,
Then, a5 = a + (5 – 1)d
=> 2 = -14 + 4d
=> 4d = 16
=> d = 4
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n – 1)d] / 2.
=> 40 = n[2(-14) + (n – 1)(4)]/2
=> 40 = n[-28 + (4n – 4)]/2
=> 40 = n[-32 + 4n]/2
=> 4n2 – 32n – 80 = 0
=> n2 – 8n – 20 = 0
=> n2 -10n + 2n – 20 = 0
=> n(n -10) + 2(n – 10 ) = 0
=> (n + 2)(n – 10) = 0
=> n = -2 or n = 10
Ignoring n = -2 as number of terms cannot be negative. So we get, n = 10.
Hence, the number of terms (n) is 10.
(iii) How many terms of the A.P. 9, 17, 25, . . . must be taken so that their sum is 636?
Solution:
Given A.P. has first term(a) = 9,
Common difference(d) = 17 – 9 = 8 and sum(Sn) = 636.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n – 1)d] / 2.
=> 636 = n[2(9) + (n − 1)(8)]/2
=> 636 = n[18 + (8n − 8)]/2
=>1271 = 10n + 8n2
=> 8n2 + 10n − 1272 = 0
=> 4n2+ 5n − 636 = 0
=> 4n2 − 48n + 53n − 636 = 0
=> 4n(n − 12) + 53(n − 12) = 0
=> (4n + 53)(n − 12) = 0
=> n = −53/4 or n = 12
Ignoring n = −53/4 as number of terms cannot be fraction. So we get, n = 12.
Hence, the number of terms (n) is 12.
(iv) How many terms of the A.P. 63, 60, 57, . . . must be taken so that their sum is 693?
Solution:
Given A.P. has first term(a) = 63,
Common difference(d) = 60 – 63 = -3 and sum(Sn) = 636.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n – 1)d] / 2.
=> 693 = n[2(63) + (n − 1)(−3)]/2
=> 693 = n[126+(−3n + 3)]/2
=> 693 = n[129 − 3n]/2
=> 129n − 3n2 = 1386
=> 3n2 − 129n + 1386 = 0
=> n2 − 43n + 462 = 0
=> n2 − 22n − 21n + 462 = 0
=> n(n − 22) − 21(n − 22) = 0
=> (n −22) (n −21) = 0
=> n = 22 or n = 21
So, the value of n can be both 21 as well as 22 because,
a22 = a + 21d = 63 + 21(− 3) = 63 − 63 = 0
Sum remains the same even if we add the 22nd term because its value is 0.
Hence, the number of terms (n) is 21 or 22.
(v) How many terms of the A.P. is 27, 24, 21. . . should be taken that their sum is zero?
Solution:
Given A.P. has first term(a) = 27,
common difference(d) = 24 − 27 = −3
and sum(Sn) = 0.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
=> 0 = n[2(27) + (n − 1)( − 3)]/2
=> 0 = n[54 + (n − 1)(-3)]
=> 0 = n[54 − 3n + 3]
=> n[57 − 3n] = 0
=> n = 0 or 3n = 57
Ignoring n = 0 as number of terms cannot be zero. So we get,
=> 3n = 57
=> n = 19
Hence, the number of terms (n) is 19.
Question 11. Find the sum of the first
(i) 11 terms of the A.P. : 2, 6, 10, 14, . . .
Solution:
Given A.P. has first term(a) = 2,
Common difference(d) = 6 − 2 = 4
and number of terms(n) = 11.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
S11 = 11[2(2) + (11 − 1)4]/2
= 11[4 + 40]/2
= 11 × 22 = 242
Hence, the sum of first 11 terms of the given A.P. is 242.
(ii) 13 terms of the A.P. : -6, 0, 6, 12, . . .
Solution:
Given A.P. has first term(a) = -6,
Common difference(d) = 0 − (−6) = 6
and number of terms(n) = 13.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
S13 = 13[2(−6) + (13 − 1)6]/2
= 13[(−12) + 72]/2
= 13[30] = 390
Hence, the sum of first 13 terms of the given A.P. is 390.
(iii) 51 terms of the A.P. : whose second term is 2 and fourth term is 8.
Solution:
Given A.P. has second term(a2) = 2,
Fourth term(a4) = 8 and
number of terms(n) = 51.
=> a2 = a + d
=> 2 = a + d …(1)
Also, a4 = a + 3d
=> 8 = a + 3d … (2)
Subtracting (1) from (2), we have
=> 2d = 6
=> d = 3
Putting d = 3 in (1), we get a = −1.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
S51 = 51[2(−1) + (51 − 1)(3)]/2
= 51[−2 + 150]/2
= 51[74] = 3774
Hence, the sum of first 51 terms of the given A.P. is 3774.
Question 12. Find the sum of
(i) the first 15 multiples of 8
Solution:
First 15 multiples of 8 are 8, 16, 24, …… , 120.
These multiples form an A.P. with first term(a) = 8,
Common difference(d) = 16 − 8 = 8
and number of terms(n) = 15.
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
S15 = 15[2(8) + (15 − 1)8]/2
= 15[16 + 112]/2
= 15[64] = 960
Hence, the sum of the first 15 multiples of 8 is 960.
(ii) the first 40 positive integers divisible by (a) 3 (b) 5 (c) 6.
Solution:
We know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
(a) First 40 positive integers divisible by 3 are 3, 6, 9, 12,…… ,120.
These integers form an A.P. with first term(a) = 3,
Common difference(d) = 6 − 3 = 3 and number of terms(n) = 40.
S40 = 40[2(3) + (40 − 1)3]/2
= 40(6 + 117)/2
= 20(123) = 2460
Hence, the sum of first 40 multiples of 3 is 2460.
(b) First 40 positive integers divisible by 5 are 5, 10, 15, 20,…… ,200.
These integers form an A.P. with first term(a) = 5,
Common difference(d) = 10 − 5 = 5 and number of terms(n) = 40.
S40 = 40[2(5) + (40 − 1)5]/2
= 40(10 + 195)/2
= 20(205) = 4100
Hence, the sum of first 40 multiples of 5 is 4100.
(c) First 40 positive integers divisible by 6 are 6, 12, 18, 24,…… ,240.
These integers form an A.P. with first term(a) = 6,
Common difference(d) = 12 − 6 = 6 and number of terms(n) = 40.
S40 = 40[2(6) + (40 − 1)6]/2
= 40(12 + 234)/2
= 20(246) = 4920
Hence, the sum of first 40 multiples of 6 is 4920.
(iii) all 3–digit natural numbers which are divisible by 13.
Solution:
All 3–digit natural numbers which are divisible by 13 are 104, 117,…… ,988.
These numbers form an A.P. with first term(a) = 104 and
Common difference(d) = 117 − 104 = 13.
We know, the nth term of an A.P. id given by, an = a + (n − 1)d.
=> 988 = 104 + (n − 1)13
=> 988 = 104 + 13n -13
=> 988 = 91 + 13n
=> 13n = 897
=> n = 69
Also, we know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
S69 = 69[2(104) + (69 − 1)13]/2
= 69[1092]/2
= 69(546) = 37674
Hence, the sum of all 3–digit natural numbers which are divisible by 13 is 37674.
(iv) all 3–digit natural numbers which are multiples of 11.
Solution:
All 3–digit natural numbers which are divisible by 11 are 110, 121, 132,…… ,990.
These numbers form an A.P. with first term(a) = 110 and
Common difference(d) = 121 − 110 = 11.
We know, the nth term of an A.P. id given by, an = a + (n − 1)d.
=> 990 = 110 + (n − 1)11
=> 990 = 110 + 11n -11
=> 990 = 99 + 11n
=> 11n = 891
=> n = 81
Also, we know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
S81 = 81[2(110) + (81 − 1)11]/2
= 81[1100]/2
= 81(550) = 44550
Hence, the sum of all 3–digit natural numbers which are divisible by 13 is 44550.
(v) all 2-digit natural numbers divisible by 4.
Solution:
All 2-digit natural numbers divisible by 4 are 12, 16, 20,…… ,96.
These numbers form an A.P. with first term(a) = 4
and common difference(d) = 16 − 12 = 4.
We know, the nth term of an A.P. is given by, an = a + (n − 1)d.
=> 96 = 12 + (n − 1)4
=> 4(n − 1) = 84
=> n − 1 = 21
=> n = 22
Also, we know sum of n terms of an A.P. is given by, Sn = n[2a + (n − 1)d] / 2.
S22 = 22[2(12) + (22 − 1)4]/2
= 22[24 + 84]/2
= 22[54] = 1188
Hence, the sum of all 2-digit natural numbers divisible by 4 is 1188.
Question 13. Find the sum:
(i) 2 + 4 + 6 + . . . + 200
Solution:
Given series is an A.P. with first term(a) = 2,
Common difference(d) = 4 − 2 = 2 and nth term(an) = 200.
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> 200 = 2 + (n − 1)2
=> 200 = 2 + 2n − 2
=> n = 200/2
=> n = 100
Also we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S100 = 100[2 + 200]/2
= 100[101] = 10100
Hence, the sum of terms of the given series is 10100.
(ii) 3 + 11 + 19 + . . . + 803
Solution:
Given series is an A.P. with first term(a) = 3,
Common difference(d) = 11 − 3 = 8 and nth term(an) = 803.
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> 803 = 3 + (n − 1)8
=> 803 = 3 + 8n − 8
=> n = 808/8
=> n = 101
Also we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S101 = 101[3 + 803]/2
= 101[403]
= 40703
Hence, the sum of terms of the given series is 40703.
(iii) (-5) + (-8) + (-11) + . . . + (-230)
Solution:
Given series is an A.P. with first term(a) = -5,
Common difference(d) = (−8) − (−5) = −3 and nth term(an) = −230.
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> −230 = −5 + (n − 1)(−3)
=> −230 = −5 − 3n + 3
=> n = 228/3
=> n = 76
Also we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S76 = 76 [−5 + (−230)]/2
= 38 x (−235) = −8930
Hence, the sum of terms of the given series is –8930.
(iv) 1 + 3 + 5 + 7 + . . . + 199
Solution:
Given series is an A.P. with first term(a) = 1,
Common difference(d) = 3 − 1 = 2 and nth term(an) = 199.
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> 199 = 1 + (n − 1)(2)
=> 199 = 1 + 2n − 2
=> n = 200/2
=> n = 100
Also we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S100 = 100[1 + 199]/2
= 50(200) = 10000
Hence, the sum of terms of the given series is 10000.
(v) 7 + 101/2 + 14 + . . . + 84
Solution:
Given series is an A.P. with first term(a) = 7,
Common difference(d) = 101/2 − 7 = (21 − 14)/2 = 7/2 and nth term(an) = 84.
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> 84 = 7 + (n − 1)(7/2)
=> 168 = 14 + 7n − 7
=> n = 161/7
=> n = 23
Also we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S23 = 23[7 + 84]/2
= 23(91)/2
= 2093/2 = 1046.5
Hence, the sum of terms of the given series is 1046.5
(vi) 34 + 32 + 30 + . . . + 10
Solution:
Given series is an A.P. with first term(a) = 34,
Common difference(d) = 32 − 34 = −2 and nth term(an) = 10.
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> 10 = 34 + (n − 1)(−2)
=> 10 = 34 − 2n + 2
=> n = (36 −10)/2
=> n = 13
Also, we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S13 = 13[34 + 10]/2
= 13(22)
= 286
Hence, the sum of terms of the given series is 286.
(vii) 25 + 28 + 31 + . . . + 100
Solution:
Given series is an A.P. with first term(a) = 25,
Common difference(d) = 28 − 25 = 3 and nth term(an) = 100.
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> 100 = 25 + (n − 1)(3)
=> 100 = 25 + 3n − 3
=> n = 88/3
=> n = 26
Also we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S26 = 26[25 + 100]/2
= 13(125)
= 1625
Hence, the sum of terms of the given series is 1625.
(viii) 18 + 151/2 + 13 + . . . + (–491/2)
Solution:
Given series is an A.P. with first term(a) = 18,
Common difference(d) = 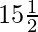 − 18 = (31 − 36)/2 = −5/2 and nth term(an) =
− 18 = (31 − 36)/2 = −5/2 and nth term(an) = 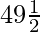
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> 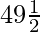 = 18+(n − 1)(−5/2)
= 18+(n − 1)(−5/2)
=> –135/2 = (n − 1)(−5/2)
=> n − 1 = 135/5
=> n = 28
Also we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S28 = 28[18 + (−491/2)]/2
= 14[−63/2]
= −441
Hence, the sum of terms of the given series is −441.
Question 14. The first and the last terms of an A.P. are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
Solution:
Given A.P. has first term(a) = 17,
Common difference(d) = 9 and last term(an) = 350.
We know nth term of an A.P. is given by, an = a + (n − 1)d.
=> 350 = 17 + (n − 1) 9
=> 350 = 17 + 9n − 9
=> 9n = 342
=> n = 38
Also we know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
S38 = 38(17 + 350)/2
= 19(367) = 6973
Hence, the number of terms of the given A.P is 38 and sum is 6973.
Question 15. The third term of an A.P. is 7 and the seventh term exceeds three times the third term by 2. Find the first term, the common difference and the sum of first 20 terms.
Solution:
Given A.P. has third term(a3) = 7 and seventh term(a7) = 3a3 + 2 = 3(7) + 2 = 23.
We know nth term of an A.P. is given by, an = a + (n − 1)d. So, we get,
a + 2d = 7 ….. (1)
a + 6d = 23 ….. (2)
Subtracting (1) from (2), we get,
=> (a + 6d) − (a + 2d) = 23 − 7
=> 4d = 16
=> d = 4
On putting d = 4 in (1), we get,
=> a + 2(4) = 7
=> a = 7 − 8
=> a = −1
We know sum of n terms of an A.P. is given by Sn = n[2a + (n − 1)d] / 2.
Here a = −1, d = −4, n = 20. So sum is,
S20 = 20[2(−1) + (20 − 1)(4)]/2
= 20[-2 + 76]/2
= 20[39] = 740
Hence, the sum of first 20 terms for the given A.P. is 740.
Question 16. The first term of an A.P. is 2 and the last term is 50. The sum of all these terms is 442. Find the common difference.
Solution:
Given A.P. has first term(a) = 2, last term(an) = 50 and sum(Sn) = 442.
We know sum of n terms of an A.P. is given by Sn = n[a + an]/2.
=> 442 = n[2 + 50]/2
=> 26n = 442
=> n = 17
Also, we know nth term of an A.P. is given by, an = a + (n − 1)d. So, we get,
=> 50 = 2 + (17 − 1)d
=> 16d = 48
=> d = 3
Hence, the common difference of the A.P. is 3.
Question 17. If 12th term of an A.P. is –13 and the sum of the first four terms is 24, what is the sum of first 10 terms?
Solution:
We are given,
12th term of the A.P., (a12) = a + 11d = −13 …. (1)
Sum of first four terms = S4 = 4[2a + (4 − 1)d]/2 = 24
=> 24 = 4[2a + 3d]/2
=> 2a + 3d = 12 ….. (2)
On multiplying eq(1) by 2 and subtracting eq(2) from it we get,
=> (2a+3d) − 2(a+11d) = 12 − 2(−13)
=> 2a + 3d − 2a − 22d = 38
=> −19d = 38
=> d = −2
On putting the value of d in eq(1), we get,
=> a + 11(−2) = −13
=> a = −13 + 22
=> a = 9
Now, sum of first 10 terms is given by,
S10 = 10[2(9) + (10 − 1)(−2)]/2
= 10(18 − 18)/2 = 0
Hence, the sum of first 10 terms of the given A.P. is 0.
Question 18. Find the sum of n terms of the series 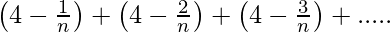
Solution:
Given A.P. has first term(a) = 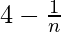
Common difference(d) = 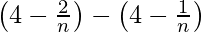
= 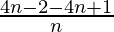
= -1/n
We know sum of n terms of an A.P. is given by Sn = n[2a + (n − 1)d] / 2
= ![Rendered by QuickLaTeX.com \frac{n}{2}\left[2\left(4-\frac{2}{n}\right)+(n-1)\left(\frac{-1}{n}\right)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7aa8e1d4b5ab3ce9696d6c1d0376a2f3_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n}{2}\left[8-\frac{2}{n}-1+\frac{1}{n}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85e0f4f23be1e47c2bd39c07d3f59bd1_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n}{2}\left[\frac{8n-2-n+1}{n}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-92cf254cda996d02eda0d9ed4179099f_l3.png)
= 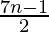
Hence, the sum of n terms of the given A.P. is 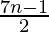
Question 19. In an A.P., if the first term is 22, the common difference is –4 and the sum to n terms is 64, find n.
Solution:
Given A.P. has first term(a) = 22, common difference(d) = −4 and sum(Sn) = 64.
We know sum of n terms of an A.P. is given by Sn = n[2a + (n − 1)d] / 2.
=> 64 = n[2(22) + (n − 1)(−4)]/2
=> 64 = n[44 − 4n + 4]/2
=> 48n − 4n2 =128
=> 4n2 − 48n + 128 = 0
=> n2 − 12n + 32 = 0
=> n2 − 8n − 4n + 32 = 0
=> n(n − 8) − 4(n − 8) = 0
=> (n − 8)(n − 4) = 0
=> n = 8 or n = 4
Hence, the number of terms are either 4 or 8.
Question 20. In an A.P., if the 5th and 12th terms are 30 and 65 respectively, what is the sum of first 20 terms?
Solution:
Given A.P. has,
Fifth term, a5 = a + 4d = 30 …..(1)
Twelfth term, a12 = a + 11d = 65 ….(2)
On subtracting eq(1) from (2), we get,
=> (a + 11d) − (a + 4d) = 65 − 30
=> 7d = 35
=> d = 5
On putting d = 5 in eq(1), we get,
=> a + 4(5) = 30
=> a = 30 − 20
=> a = 10
We know sum of n terms of an A.P. is given by Sn = n[2a + (n − 1)d] / 2.
Here a = 10, d = 5 and n = 20. So we get,
S20 = 20[2(10) + (20 − 1)(5)]/2
= 20[20 + 95]/2
= 10[115] = 1150
Hence, the sum of first 20 terms for the given A.P. is 1150.
Question 21. Find the sum of first 51 terms of an A.P. whose second and third terms are 14 and 18 respectively.
Solution:
Given A.P. has,
Second term, a2 = a + d = 14 …..(1)
Third term, a3 = a + 2d = 18
Hence, common difference(d) = a3 − a2 = 18 − 14 = 4.
On putting d = 4 in (1), we get,
=> a + 4 = 14
=> a = 10
We know sum of n terms of an A.P. is given by Sn = n[2a + (n − 1)d] / 2.
Here a = 10, d = 4 and n = 51. So we get,
S51 = 51[2(10) + (51 − 1)(4)]/2
= 51[20 + 200]/2
= 51[110] = 5610
Hence, the sum of first 51 terms for the given A.P. is 5610.
Question 22. If the sum of 7 terms of an A.P. is 49 and that of 17 terms is 289, find the sum of n terms.
Solution:
We know sum of n terms of an A.P. is given by Sn = n[2a + (n − 1)d]/2.
So we get, S7 = 49
=> 7[2a + (7 − 1)d]/2 = 49
=> 7[a + 3d] = 49
=> a + 3d = 7 ….. (1)
And also, S17 = 289
=> 17[2a + (17 − 1)d]/2 = 289
=> 17[a + 8d] = 289
=> a + 8d = 17 ….. (2)
On subtracting eq(1) from (2), we get,
=> a + 8d − (a + 3d) = 17 − 7
=> 5d = 10
=> d = 2
On putting d = 2 in (1), we get,
=> a + 3(2) = 7
=> a = 1
Here a = 1, d = 2, so sum of n terms would be,
Sn = n[2(1) + (n − 1)(2)]/2
= n[2 + 2n − 2]/2
= n[n] = n2
Hence, the sum of n terms of the given A.P is n2.
Question 23. The first term of an A.P. is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Solution:
Given A.P. has first term(a) = 5, last term(an) = 45 and sum(Sn) = 400.
We know sum of n terms of an A.P. is given by, Sn = n[a + an]/2
=> 400 = n[5 + 45]/2
=> 50n = 800
=> n = 16
Also, we know nth term of an A.P. given by, an = a + (n − 1)d.
=> 45 = 5 + (16 − 1)d
=> 15d = 40
=> d = 8/3
Hence, the number of terms of given A.P. is 16 and common difference is 8/3.
Question 24. In an A.P. the first term is 8, nth term is 33 and the sum of first n terms is 123. Find n and the d, the common difference.
Solution:
Given A.P. has first term(a) = 8, nth term(an) = 33 and sum(Sn) = 123.
We know sum of n terms of an A.P. is given by, Sn = n[a + an]/2
=> 123 = n[8 + 33]/2
=> 41n = 246
=> n = 6
Also, we know nth term of an A.P. given by, an = a + (n − 1)d.
=> 33 = 8 + (6 − 1)d
=> 5d = 25
=> d = 5
Hence, the number of terms of given A.P. is 6 and common difference is 5.
Share your thoughts in the comments
Please Login to comment...