Question 1: A coin is tossed. Find the total number of elementary events and also the total number of events associated with the random experiment.
Solution:
Given:
A coin is tossed.
When a coin is tossed, there will be two possible outcomes, that is Head (H) and Tail (T).
Since, the number of elementary events is 2-{H, T}
as we know that, if there are ‘n’ elements in a set, then the number of total element in its subset is 2n.
So, the total number of the experiment is 4,
There are 4 subset of S = {H}, {T}, {H, T} and Փ
Therefore,
There are total 4 events in a given experiment.
Question 2: List all events associated with the random experiment of tossing of two coins. How many of them are elementary events?
Solution:
Given:
Two coins are tossed once.
As we know that, when two coins are tossed then the number of possible outcomes are 22 = 4
So,
The Sample spaces are {HH, HT, TT, TH}
Therefore,
There are total 4 events associated with the given experiment.
Question 3: Three coins are tossed once. Describe the following events associated with this random experiment:
A = Getting three heads, B = Getting two heads and one tail, C = Getting three tails, D = Getting a head on the first coin.
(i) Which pairs of events are mutually exclusive?
(ii) Which events are elementary events?
(iii) Which events are compound events?
Solution:
Given:
There are three coins tossed once.
When three coins are tossed, then the sample spaces are:
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
So, as the question says,
A = {HHH}
B = {HHT, HTH, THH}
C = {TTT}
D = {HHH, HHT, HTH, HTT}
Now,
A⋂ B = Փ,
A ⋂ C = Փ,
A ⋂ D = {HHH}
B ⋂ C = Փ,
B ⋂ D = {HHT, HTH}
C ⋂ D = Փ
As we know that, if the intersection of two sets are null or empty it means both the sets are Mutually Exclusive.
(i) Events A and B, Events A and C, Events B and C and events C and D are mutually exclusive.
(ii) Now, as we know that, if an event has only one sample point of a sample space, then it is called elementary events.
Thus, A and C are elementary events.
(iii) If there is an event that has more than one sample point of a sample space, it is called a compound event.
Since, B ⋂ D = {HHT, HTH}
Thus, B and D are compound events.
Question 4: In a single throw of a die describe the following events:
(i) A = Getting a number less than 7
(ii) B = Getting a number greater than 7
(iii) C = Getting a multiple of 3
(iv) D = Getting a number less than 4
(v) E = Getting an even number greater than 4.
(vi) F = Getting a number not less than 3.
Also, find A ∪ B, A ∩ B, B ∩ C, E ∩ F, D ∩ F and
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
Solution:
Given:
A dice is thrown once.
Now, find the given events, and also find A ∪ B, A ∩ B, B ∩ C, E ∩ F, D ∩ F and 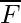
S = {1, 2, 3, 4, 5, 6}
According to the question, we have certain events as:
(i) A = Getting a number below 7
Thus, the sample spaces for A are:
A = {1, 2, 3, 4, 5, 6}
(ii) B = Getting a number greater than 7
Thus, the sample spaces for B are:
B = {Փ}
(iii) C = Getting multiple of 3
Thus, the Sample space of C is
C = {3, 6}
(iv) D = Getting a number less than 4
Thus, the sample space for D is
D = {1, 2, 3}
(v) E = Getting an even number greater than 4.
Thus, the sample space for E is
E = {6}
(vi) F = Getting a number not less than 3.
Thus, the sample space for F is
F = {3, 4, 5, 6}
Here,
A = {1, 2, 3, 4, 5, 6} and B = {Փ}
A ⋃ B = {1, 2, 3, 4, 5, 6}
A = {1, 2, 3, 4, 5, 6} and B = {Փ}
A ⋂ B = {Փ}
B = {Փ} and C = {3, 6}
B ⋂ C = {Փ}
F = {3, 4, 5, 6} and E = {6}
E ⋂ F = {6}
E = {6} and D = {1, 2, 3}
D ⋂ F = {3}
Question 5: Three coins are tossed. Describe
(i) two events A and B which are mutually exclusive.
(ii) three events A, B, and C which are mutually exclusive and exhaustive.
(iii) two events A and B which are not mutually exclusive.
(iv) two events A and B which are mutually exclusive but not exhaustive.
Solution:
Given:
Three coins are tossed.
When three coins are tossed, then the sample spaces are
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Here,
(i) The two events which are mutually exclusive are when,
A: getting no tails
B: getting no heads
Then,
A = {HHH} and B = {TTT}
So, the intersection of this set will be null. Or, the sets are disjoint.
(ii) Three events which are mutually exclusive and exhaustive are:
A: getting no heads
B: getting exactly one head
C: getting at least two head
Thus,
A = {TTT}
B = {TTH, THT, HTT} and,
C = {HHH, HHT, HTH, THH}
Hence,
A ⋃ B = B ⋂ C = C ⋂ A = Փ and
A⋃ B⋃ C = S
(iii) The two events that are not mutually exclusive are:
A: getting three heads
B: getting at least 2 heads
So,
A = {HHH}
B = {HHH, HHT, HTH, THH}
Hence, A ⋂ B = {HHH} = Փ
(iv) The two events which are mutually exclusive but not exhaustive are:
A: getting exactly one head
B: getting exactly one tail
So,
A = {HTT, THT, TTH} and B = {HHT, HTH, THH}
It is because A ⋂ B = Փ but A⋃ B ≠ S
Question 6: A die is thrown twice. Each time the number appearing on it is recorded. Describe the following events:
(i) A = Both numbers are odd.
(ii) B = Both numbers are even
(iii) C = sum of the numbers is less than 6.
Also, find A ∪ B, A ∩ B, A ∪ C, A ∩ C. Which pairs of events are mutually exclusive?
Solution:
Given:
A dice is thrown twice. Each time number appearing on it is recorded.
When a dice is thrown twice then the number of sample spaces are 62 = 36
Here,
The possibility both odd numbers are:
A = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}
Thus, possibility of both even numbers is:
B = {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)}
And, possible outcome of sum of the numbers is less than 6.
C = {(1, 1)(1, 2)(1, 3)(1, 4)(2, 1)(2, 2)(2, 3)(3, 1)(3, 2)(4, 1)}
Hence,
(AՍB) = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5) (2, 2)(2, 4)(2, 6)(4, 2)(4, 4)(4, 6)(6, 2)(6, 4)(6, 6)}
(AՌB) = {Փ}
(AUC) = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5) (1, 2)(1, 4)(2, 1)(2, 2)(2, 3)(3, 1)(3, 2)(4, 1)}
(AՌC) = {(1, 1), (1, 3), (3, 1)}
Therefore,
(AՌB) = Փ and (AՌC) ≠ Փ, A and B are mutually exclusive, but A and C are not.
Question 7: Two dice are thrown. the events A, B, C, D, E, and F are described as follows:
A=Getting an even number on the first die.
B=Getting an odd number on the first die.
C=Getting at most 5 as sum of the number on the two dice.
D=Getting the sum of the numbers on the dice greater than 5 but less than 10.
E=Getting at least 10 as the sum of the numbers on the dice.
F=Getting an odd number on one of the dice.
(i) Describe the following events:
A and B, B or C, B and C, A and E, A or F, A and F
(ii) State true or false:
(a) A and B are mutually exclusive
(b) A and B are mutually exclusive and exhaustive events.
(c) A and C are mutually exclusive events.
(d) C and D are mutually exclusive and exhaustive events.
(e) C, D, and E are mutually exclusive and exhaustive events.
(f) A’ and B’ are mutually exclusive events.
(g) A, B, F are mutually exclusive and exhaustive events.
Solution:
A = Getting an even number on the first die.
A = {(2, 1), (2, 2) (2, 3), (2, 4), (2, 5), (2, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
B = Getting an odd number on the first die.
B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
C = Getting at most 5 as sum of the numbers on the two dice.
C = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
D = Getting the sum of the numbers on the dice > 5 but < 10.
D = {(1, 5) (1, 6), (2, 4), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3)}
F = Getting an odd number on one of the dice.
F = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5)}
Its clear that A and B are mutually exclusive events and A ∩ B = ∅
B ∪ C = {(1, 1), (1,2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3,3), (3, 4), (3, 6), (5, 1), (5, 2), (5, 3), (5, 5), (5, 6), (2,1), (2,2), (2, 3), (4, 1)}
B ∩ C = {(1, 1), (1, 2), (1, 3), (1, 4), (3, 1), (3, 2)}
A ∩ E = {(4, 6), (6, 4), (6, 5), (6, 6)}
A ∪ F = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (5, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
A ∩ F = {(2, 1), (2,3), (2,5), (4,1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5)}
(ii)
a) True, A ∩ B = ∅
b) True, A ∩ B = ∅ and A ∪ B = S
c) False, A ∩ C ≠ ∅
d) False, A ∩ B = ∅ and A ∪ B ≠ S
e) True, C ∩ D = D ∩ E = C ∩ E = Φ and C ∪ D ∪ E = S
f) True, A’ ∩ B’ = ∅
g) False, A ∩ F ≠ ∅
Question 8: The number 1, 2, 3, and 4 are written separately on four slips of paper. The slips are then put in a box and mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. describe the following events:
A=The numbers on the first slip is larger than the one on the second slip.
B =The number on the second slip is greater than 2
C=The sum of the numbers on the two slips is 6 or 7
D=The number on the second slips is twice that on the first slip.
Which pair(s) of events is (are) mutually exclusive?
Solution:
We have four slips of paper with numbers 1, 2, 3 & 4.
A person draws two slips without replacement.
∴ Number of elementary events = 4C2
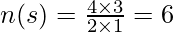
A = The number on the first slip is larger than the one on the second slip
A = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}
B = The number on the second slip is greater than 2
Therefore,
B = {(1,3), (2,3) , (1,4), (2, 4), (3, 4), (4,3)}
C = The sum of the numbers on the two slips is 6 or 7
Therefore,
C = {(2, 4), (3, 4), (4, 2), (4, 3)}
and,
D = The number on the second slips is twice that on the first slip
D = {(1, 2), (2, 4)}
and, A and D form a pair of mutually exclusive events as A ∩ B = ∅
Question 9: A card is picked up from a deck of 52 playing cards.
(i) What is the sample space of the experiment?
(ii) What is the event that the chosen card is ace faced card?
Solution:
(i) Sample space for picking up a card from a set of 52 cards is set of 52 cards itself.
(ii) For an event of chosen card be black faced card, event is a set of jack, king, queen of spades and clubs,
Share your thoughts in the comments
Please Login to comment...