Class 11 RD Sharma Solutions – Chapter 10 Sine and Cosine Formulae and Their Applications – Exercise 10.2 | Set 1

Question 1. In a ∆ABC, if a = 5, b = 6 and C = 60^o, show that its area is (15√3)/2 sq. units.

Solution:

We are given a = 5, b = 6 and C = 60^o. 

Now we know the area of a ∆ABC is given by 1/2 ab sin C where, a and b are the lengths of the sides of a triangle and C is the angle between these sides.

So, area of ∆ABC = (1/2) 5(6) sin 60^o

= (1/2) (5) (6) (√3/2)

= 15√3/2 sq. units

Hence, proved.

Question 2. In a ∆ABC, if a = √2, b = √3 and c = √5 show that its area is √6/2 sq. units.

Solution:

We are given a = √2, b = √3 and c = √5. 

According to Cosine formula, cos C = (a² + b² – c²)/2ab

= (2 + 3 – 5)/2√6

= 0

So, sin C = √(1–cos² C) = 1

Now we know the area of a ∆ABC is given by 1/2 ab sin C where, a and b are the lengths of the sides of a triangle and C is the angle between these sides.

Therefore, area of ∆ABC = (1/2) (√2) (√3) (1)

= √6/2 sq. units.

Hence, proved.

Question 3. The sides of a triangle are a = 4, b = 6 and c = 8, show that: 

8 cos A + 16 cos B + 4 cos C = 17

Solution:

We are given a = 4, b = 6 and c = 8.

According to Cosine formula, cos A = (b² + c² – a²)/2bc

= (36 + 64 – 16)/96

= 84/96

= 7/8

Also, cos B = (a² + c² – b²)/2ac

= (16 + 64 – 36)/64

= 44/64

= 11/16

Also, cos C = (a² + b² – c²)/2ab

= (16 + 36 – 64)/48

= –12/48

= –1/4

Here, L.H.S. = 8 cos A + 16 cos B + 4 cos C 

= 8 × (7/8) + 16 × (11/16) + 4 × (–1/4) 

= 7 + 11 – 1

= 17

= R.H.S.

Hence, proved.

Question 4. In a ∆ABC, if a = 18, b = 24, c = 30, find cos A, cos B and cos C.

Solution: 

We are given a = 18, b = 24 and c = 30.  

According to Cosine formula, cos A = (b² + c² – a²)/2bc

= (24² + 30² – 18²)/2(24)(30)

= (576 + 900 – 324)/1440

= 1152/1440

= 4/5

Also, cos B = (a² + c² – b²)/2ac

= (324 + 900 – 576)/2(18)(30)

= 648/1080

= 3/5

Also, cos C = (a² + b² – c²)/2ab

= (324 + 576 – 900)/2(18)(24)

= 0

Therefore, the values of cos A, cos B and cos C are 4/5, 3/5 and 0 respectively.

Question 5. For any ΔABC, show that b (c cos A – a cos C) = c² – a²

Solution:

According to Cosine formula, 

cos A = (b² + c² – a²)/2bc

=> bc cos A = (b² + c² – a²)/2 . . . . (1)

Also, cos C = (a² + b² – c²)/2ab

=> ab cos C = (a² + b² – c²)/2 . . . . (2)

Subtracting (2) from (1), we get,

L.H.S. = bc cos A – ab cos C = (b² + c² – a²)/2 – (a² + b² – c²)/2

= (b² + c² – a² – a² – b² + c²)/2

= (2c² – 2a²)/2

= c² – a²

= R.H.S.

Hence, proved.

Question 6. For any ΔABC show that c (a cos B – b cos A) = a² – b²

Solution:

According to Cosine formula,

cos B = (a² + c² – b²)/2ac

=> ac cos B = (a² + c² – b²)/2  . . . . (1)

Also cos A = (b² + c² – a²)/2bc

=> bc cos A = (b² + c² – a²)/2  . . . . (2)

Subtracting (2) from (1), we get,

L.H.S. = ac cos B – bc cos A = (a² + c² – b²)/2 – (b² + c² – a²)/2

= (a² + c² – b² – b² – c² + a²)/2  

= (2a² – 2b²)/2

= a² – b²

= R.H.S.

Hence, proved.

Question 7. For any ΔABC show that 2 (bc cos A + ca cos B + ab cos C) = a² + b² + c²

Solution:

According to Cosine formula,

cos A = (b² + c² – a²)/2bc

=> 2bc cos A = b² + c² – a²  . . . . (1)

Also, cos B = (a² + c² – b²)/2ac

=> 2ac cos B = a² + c² – b² . . . . (2)

Also, cos C = (a² + b² – c²)/2ab

=> 2ab cos C = a² + b² – c² . . . . (3)

Adding (1), (2) and (3), we get,

L.H.S. = 2bc cos A + 2ac cos B + 2ab cos C 

= b² + c² – a² + a² + c² – b² + a² + b² – c²

= a² + b² + c²

= R.H.S.

Hence, proved.

Question 8. For any ΔABC show that (c² + b² – a²) tan A = (a² + c² – b²) tan B = (a² + b² – c²) tan C

Solution:

According to sine rule in ΔABC,

sin A/a = sin B/b = sin C/c = k (constant) 

According to Cosine formula,

cos A = (b² + c² – a²)/2bc

2bc cos A = (b² + c² – a²)

(b² + c² – a²) tan A = 2bc cos A tan A 

= 2bc sin A

= 2kabc . . . . (1)

Also, cos B = (a² + c² – b²)/2ac

2ac cos B = (a² + c² – b²)  

(a² + c² – b²) tan B = 2ac cos B tan B

= 2ac sin B

= 2kabc . . . . (2)

Also, cos C = (a² + b² – c²)/2ab

2ab cos C = (a² + b² – c²)  . . . . (3)

(a² + b² – c²) tan C = 2ab cos C tan C

= 2ab sin C

= 2kabc . . . . (3)

From (1), (2) and (3), we get,

(c² + b² – a²) tan A = (a² + c² – b²) tan B = (a² + b² – c²) tan C

Hence, proved.

Question 9. For any ΔABC show that: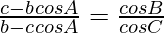

Solution:

According to sine rule in ΔABC,

a/sin A = b/sin B = c/sin C = k (constant) 

Here, L.H.S. =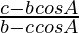 

= 

= 

= 

= 

= 

= 

= 

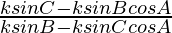
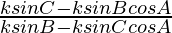
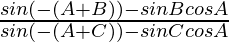
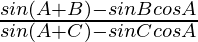
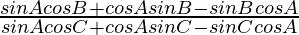
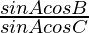
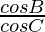
= R.H.S.

Hence, proved.

Question 10. For any ΔABC show that: 

a(cos B + cos C – 1) + b(cos C + cos A – 1) + c(cos A + cos B – 1) = 0

Solution:

According to projection formula, we get,

a = b cos C + c cos B

b = c cos A + a cos C

c = a cos B + b cos A

Here, L.H.S. = a(cos B + cos C – 1) + b(cos C + cos A – 1) + c(cos A + cos B – 1)

= a cos B + a cos C – a + b cos C + b cos A – b + c cos A + c cos B – c

= c – b cos A + a cos C – a + a – c cos B + b cos A – b + b – a cos C + c cos B – c

= 0

= R.H.S.

Hence, proved.