Class 11 RD Sharma Solutions – Chapter 30 Derivatives – Exercise 30.5 | Set 1
Last Updated :
30 Apr, 2021
Differentiate the following functions with respect to x:
Question 1. 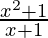
Solution:
By using quotient rule, we get,

= 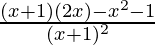
= 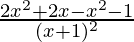
= 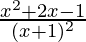
= 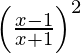
Question 2. 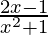
Solution:
By using quotient rule, we get,
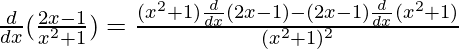
= 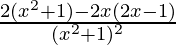
= 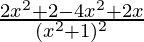
= 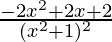
= 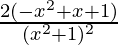
Question 3. 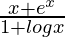
Solution:
By using quotient rule, we get,
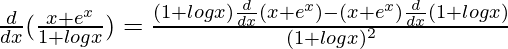
= 
= 
= 
= 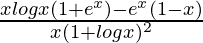
Question 4. 
Solution:
By using quotient rule, we get,
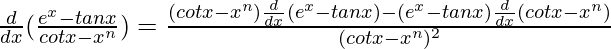
= 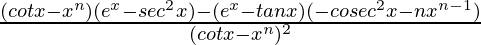
= 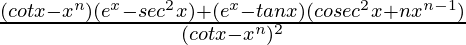
Question 5. 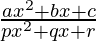
Solution:
By using quotient rule, we get,
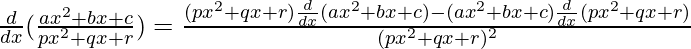
= 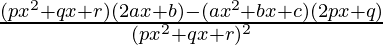
= 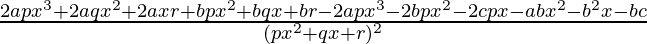
= 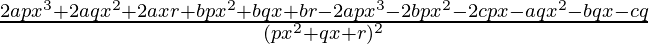
= 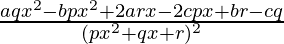
= 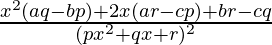
Question 6. 
Solution:
By using quotient rule, we get,
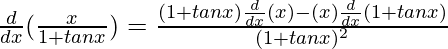
= 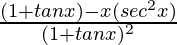
= 
Question 7. 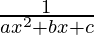
Solution:
By using quotient rule, we get,
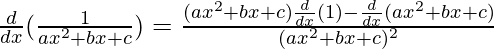
= 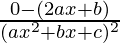
= 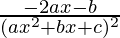
Question 8. 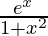
Solution:
By using quotient rule, we get,
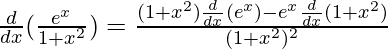
= 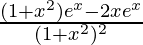
= 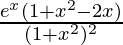
= 
Question 9. 
Solution:
By using quotient rule, we get,

= 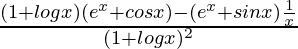
= 
Question 10. 
Solution:
By using quotient rule, we get,
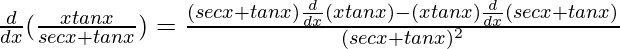
= 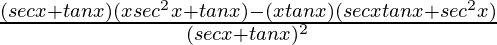
= 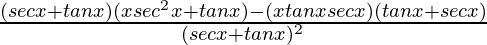
= 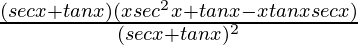
= 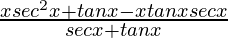
= 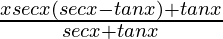
Question 11. 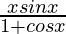
Solution:
By using quotient rule, we get,

= 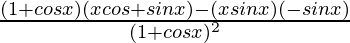
= 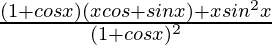
= 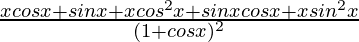
= 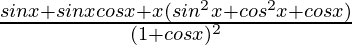
= 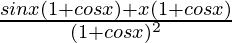
= 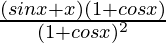
= 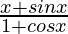
Question 12. 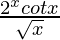
Solution:
By using quotient rule, we get,
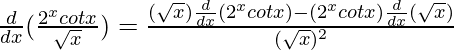
= 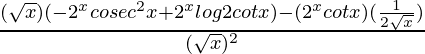
= 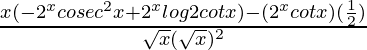
= 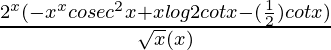
= 
Question 13. 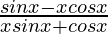
Solution:
By using quotient rule, we get,

= 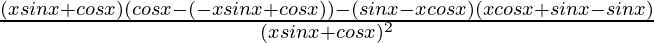
= 
= 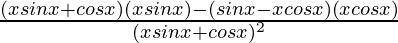
= 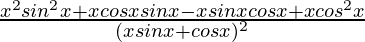
= 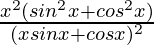
= 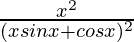
Question 14. 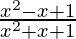
Solution:
By using quotient rule, we get,
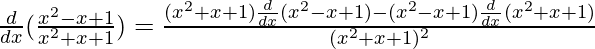
= 
= 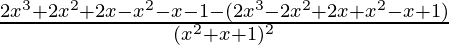
= 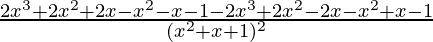
= 
= 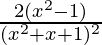
Question 15. 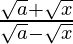
Solution:
By using quotient rule, we get,
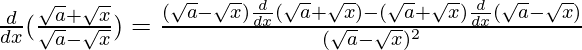
= 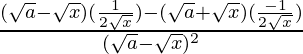
= 
= 
= 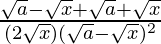
= 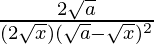
= 
Share your thoughts in the comments
Please Login to comment...