Class 11 NCERT Solutions- Chapter 13 Limits And Derivatives – Miscellaneous Exercise on Chapter 13 | Set 1
Last Updated :
30 Aug, 2022
Question 1: Find the derivative of the following functions from first principle:
(i) -x
Solution:
f(x) = -x
f(x+h) = -(x+h)
From the first principle,
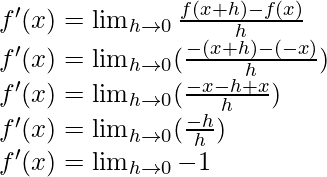
f'(x) = -1
(ii) (-x)-1
Solution:
f(x) = (-x)-1 = 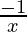
f(x+h) = (-(x+h))-1 = 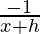
From the first principle,
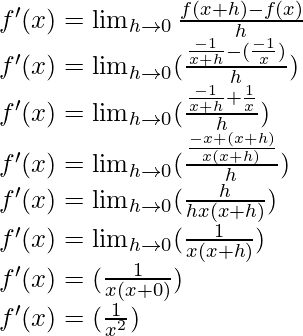
(iii) sin(x+1)
Solution:
f(x) = sin(x+1)
f(x+h) = sin((x+h)+1)
From the first principle,
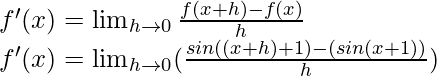
Using the trigonometric identity,
sin A – sin B = 2 cos 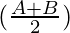 sin
sin 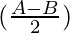
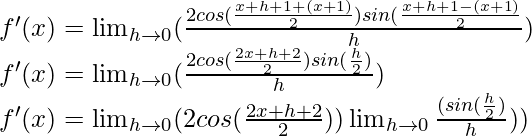
Multiply and divide by 2, we have
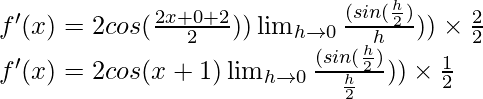
f'(x) = cos (x+1) (1)
f'(x) = cos (x+1)
(iv) 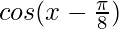
Solution:
Here, 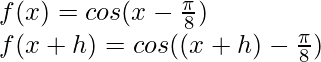
From the first principle,
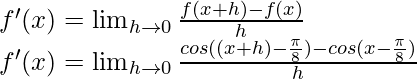
Using the trigonometric identity,
cos a – cos b = -2 sin 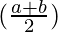 sin
sin 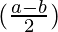
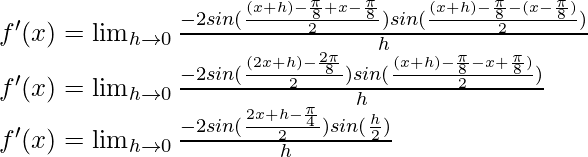
Multiplying and dividing by 2,

Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Question 2: (x+a)
Solution:
f(x) = x+a
Taking derivative both sides,
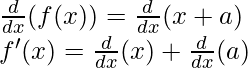
As, the derivative of xn is nxn-1 and derivative of constant is 0.
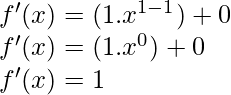
Question 3: 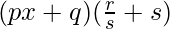
Solution:
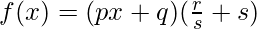
Taking derivative both sides,
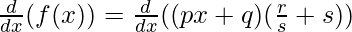
Using the product rule, we have
(uv)’ = uv’+u’v
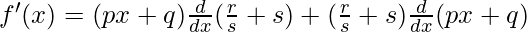
As, the derivative of xn is nxn-1 and derivative of constant is 0.
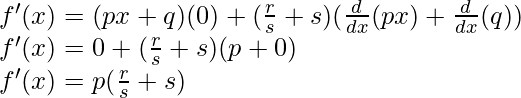
Question 4: (ax+b) (cx+d)2
Solution:
f(x) = (ax+b) (cx+d)2
Taking derivative both sides,
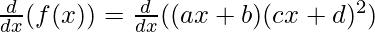
Using the product rule, we have
(uv)’ = uv’+u’v
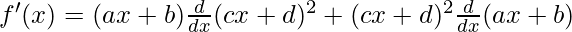
As, the derivative of xn is nxn-1 and derivative of constant is 0.
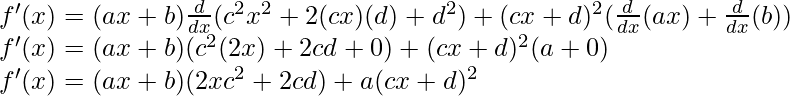
Question 5: 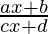
Solution:
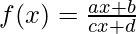
Taking derivative both sides,
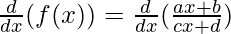
Using the quotient rule, we have
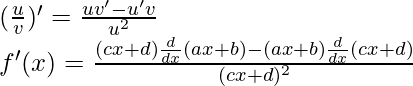
As, the derivative of xn is nxn-1 and derivative of constant is 0.
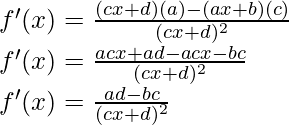
Question 6: 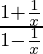
Solution:
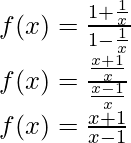
Taking derivative both sides,
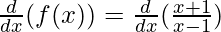
Using the quotient rule, we have
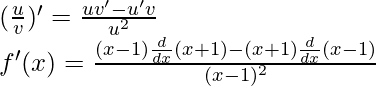
As, the derivative of xn is nxn-1 and derivative of constant is 0.
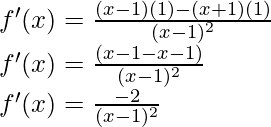
Question 7: 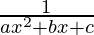
Solution:
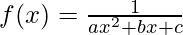
Taking derivative both sides,
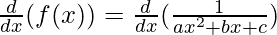
Using the quotient rule, we have
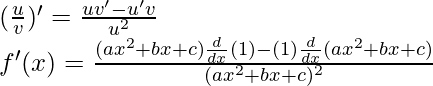
As, the derivative of xn is nxn-1 and derivative of constant is 0.
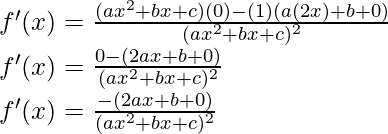
Question 8: 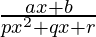
Solution:
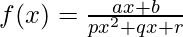
Taking derivative both sides,
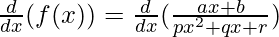
Using the quotient rule, we have
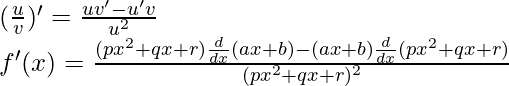
As, the derivative of xn is nxn-1 and derivative of constant is 0.
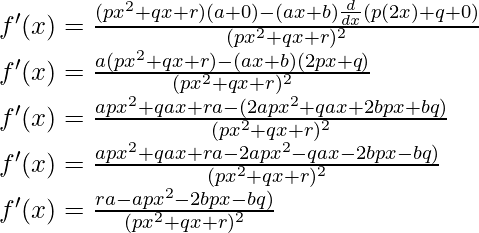
Question 9: 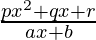
Solution:
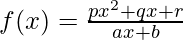
Taking derivative both sides,
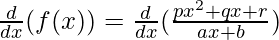
Using the quotient rule, we have
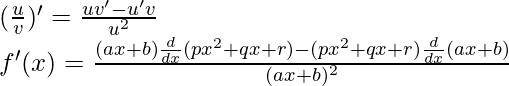
As, the derivative of xn is nxn-1 and derivative of constant is 0.
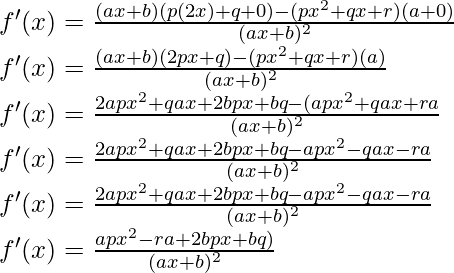
Question 10: 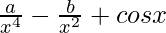
Solution:
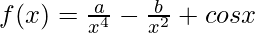
Taking derivative both sides,
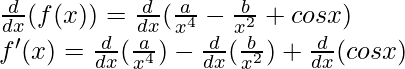
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = a \frac{d}{dx}(x^{-4}) - b\frac{d}{dx}(x^{-2})+(- sin x)\\ f'(x) = a (-4x^{-4-1}) - b((-2)x^{-2-1})+(- sin x)\\ f'(x) = a (-4x^{-5}) - b((-2)x^{-3})+(- sin x)\\ f'(x) = -[4ax^{-5} - 2bx^{-3} + sin x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ab5d3ca2f48977416005ce986aa7ee7_l3.png)
Question 11: 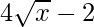
Solution:
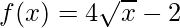
Taking derivative both sides,
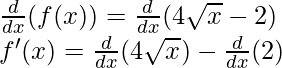
As, the derivative of xn is nxn-1 and derivative of constant is 0.
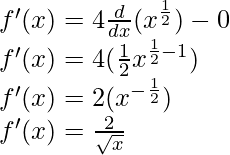
Question 12: (ax+b)n
Solution:
f(x) = (ax+b)n
f(x+h) = (a(x+h)+b)n
f(x+h) = (ax+ah+b)n
From the first principle,
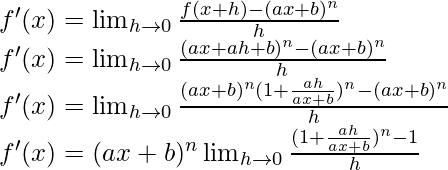
Using the binomial expansion, we have
![Rendered by QuickLaTeX.com f'(x) = (ax+b)^n \lim_{h \to 0} \frac{[1+n(\frac{ah}{ax+b}+\frac{n(n-1)}{2!}(\frac{ah}{(ax+b)^2}+.....]-1}{h}\\ f'(x) = (ax+b)^n \lim_{h \to 0} \frac{[n(\frac{ah}{ax+b}+\frac{n(n-1)a^2h^2}{2!(ax+b)^2}+.................]}{h}\\ f'(x) = (ax+b)^n \lim_{h \to 0} [n(\frac{a}{ax+b}+\frac{n(n-1)a^2h}{2!(ax+b)^2}+.................]\\ f'(x) = (ax+b)^n [n(\frac{a}{ax+b}+\frac{n(n-1)a^2(0)}{2!(ax+b)^2}+0+0+0......]\\ f'(x) = (ax+b)^n (\frac{na}{ax+b})\\ f'(x) = na (ax+b)^{n-1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5111de4b3cabfb330f5fa7ccfbc4c249_l3.png)
Question 13: (ax+b)n (cx+d)m
Solution:
f(x) = (ax+b)n (cx+d)m
Taking derivative both sides,
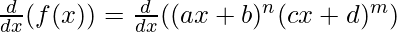
Using the product rule, we have
(uv)’ = uv’+u’v
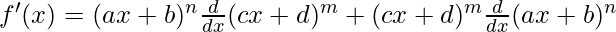
Let’s take, g(x) = (cx+d)m
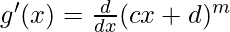
g(x+h) = (c(x+h)+d)m
g(x+h) = (cx+ch+d)m
From the first principle,
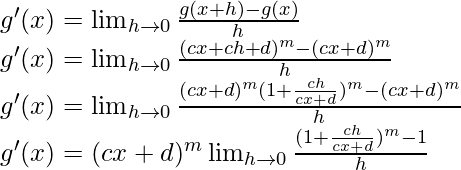
Using the binomial expansion, we have
![Rendered by QuickLaTeX.com g'(x) = (cx+d)^m \lim_{h \to 0} \frac{[1+m(\frac{ch}{cx+d}+\frac{m(m-1)}{2!}(\frac{ch}{(cx+d})^2+.....)]-1}{h}\\ g'(x) = (cx+d)^m \lim_{h \to 0} \frac{[m(\frac{ch}{cx+d}+\frac{m(nm-1)c^2h^2}{2!(cx+d)^2}+.................)]}{h}\\ g'(x) = (cx+d)^m \lim_{h \to 0} [m(\frac{c}{cx+d}+\frac{m(m-1)c^2h}{2!(cx+d)^2}+.................)]\\ g'(x) = (cx+d)^m [m(\frac{c}{cx+d}+\frac{m(m-1)c^2(0)}{2!(cx+d)^2}+0+0+0......)]\\ g'(x) = (cx+d)^m (\frac{mc}{cx+d})\\ g'(x) = mc (cx+d)^{m-1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c778c55d5223983e04e541b252d9202_l3.png)
So, as
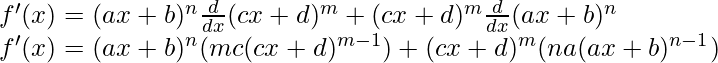
Question 14: sin (x + a)
Solution:
f(x) = sin(x+a)
f(x+h) = sin((x+h)+a)
From the first principle,
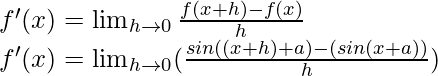
Using the trigonometric identity,
sin A – sin B = 2 cos 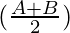 sin
sin 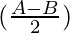
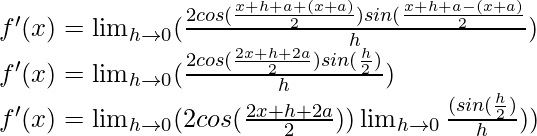
Multiply and divide by 2, we have
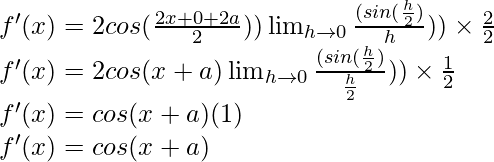
Question 15: cosec x cot x
Solution:
f(x) = cosec x cot x
Taking derivative both sides,
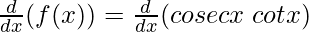
Using the product rule, we have
(uv)’ = uv’+u’v
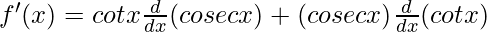
f'(x) = cot x (-cot x cosec x) + (cosec x) (-cosec2 x)
f'(x) = – cot2 x cosec x – cosec3 x
Share your thoughts in the comments
Please Login to comment...