Class 11 RD Sharma Solutions – Chapter 23 The Straight Lines- Exercise 23.13
Last Updated :
28 Mar, 2021
Question 1: Find the angles between each of the following pairs of straight lines.
(i) 3x+y+12=0 and x+2y-1=0
Solution:
Given equations of lines are,3x + y + 12 = 0, x + 2y -1 = 0
Letm1 andm2 be the slopes of these lines respectively.
By y = mx +c, we getm1=-3 and m2=-1/2
Let θ be the angle between the two lines,
By using formula 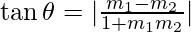
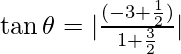
⇒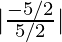
⇒ 1
Therefore,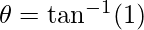
The angles between the two lines is 45°.
(ii) 3x-y+5 = 0 and x-3y+1 = 0
Solution:
Given equations of lines are 3x – y + 5 = 0, x – 3y +1 = 0
Let m1 and m2 be the slopes of these lines respectively.
By y = mx +c, we get m1=3 and m2=1/3
Let θ be the angle between the two lines,
We know that,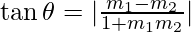
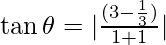
⇒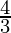
Therefore,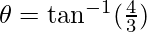
The angle between the two lines is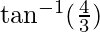
(iii) 3x+4y -7 = 0 and 4x-3y+5 = 0
Solution:
Given equations of lines are 3x + 4y – 7 = 0, 4x – 3y+5 = 0
Letm1 andm2 be the slopes of these lines respectively.
By y= mx +c, we get m1 = 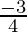 and m2 =
and m2 = 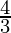
Here, if we carefully observe, m1m2 = -1, which means
From the formula, 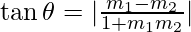 denominator will become 0,
denominator will become 0,
Therefore, 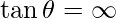 ,
,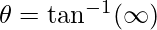
The angle between the two lines is 90°.
(iv) x-4y = 3 and 6x-y = 11
Solution:
Given equations of lines are x – 4y =3, 6x – y =11
Letm1 andm2 be the slopes of these lines respectively.
By y = mx +c, we get, m1=1/4 and m2=6
Let θ be the angle between the two lines,
We know that,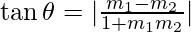
⇒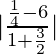
⇒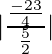
⇒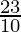
Therefore,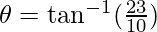
The angle between the two lines is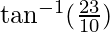
(v) (m2-mn)y = (mn+n2)x + n3 and (mn+m2)y = (mn-n2)x + m3
Solution:
Given two lines, letm1 andm2 be the slopes of these lines.
By y = mx +c, we getm1 = 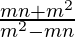 and m2 =
and m2 = 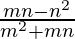
Let θ be the angle between two lines,
We know that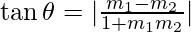
⇒ 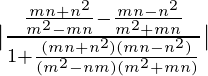
⇒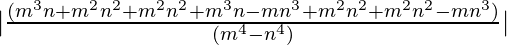
⇒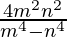
Therefore, Angle between two lines is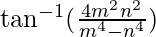 .
.
Question 2: Find the acute angle between the lines 2x-y+3 = 0 and x+y+2 = 0
Solution:
Letm1 andm2 be the slopes of these two lines
By y = mx +c, we get m1=2 and m2=-1
Let θ be the angle between the two lines,
We know that,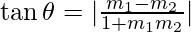
⇒ 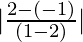
⇒ 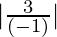
Here we need acute angle,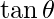 is positive if the angle is acute and negative if obtuse.
is positive if the angle is acute and negative if obtuse.
Therefore,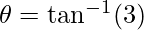 .
.
The acute angle between the two lines is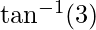 .
.
Question 3: Prove that points (2, -1), (0, 2), (2, 3), and (4, 0) are the coordinates of the vertices of a parallelogram and find the angle between its diagonals.
Solution:
Let the given points are A = (2,-1), B = (0, 2), C = (2, 3) and D = (4, 0) are coordinates of a parallelogram.
For these points to form a parallelogram, it is must that any pair of two lines formed by these points are parallel to each other.
So, Now lets find the slopes of lines AB, BC, CD, DA using formula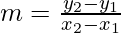
Slope of line 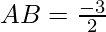
Slope of line 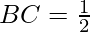
Slope of line 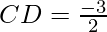
Slope of line 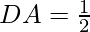
Since the lines AB parallel to CD and BC parallel to DA, the points form a parallelogram.
Now, Angle between the diagonals of parallelogram = Angle between the lines AC and BD.

Letm1 andm2 be the slopes of these lines,
From the figure, the angle between diagonals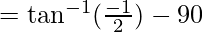
We know that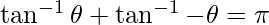
⇒ 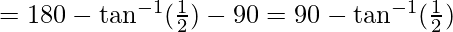
Therefore, The angle between the diagonals is 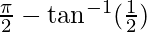
Question 4: Find the angles between the line joining the points (2, 0), (0, 3), and the line x + y = 1.
Solution:
Let slope of line joining the points (2, 0) and (0, 3) is m1 = -3/2
slope of line m2 =-1
Let θ be the angle between the two lines,
We know that,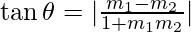
⇒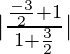
⇒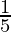
Therefore, the acute angle between the line and the line joining the points is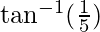
Question 5: If θ is the angle which the straight line joining the points (x1,y1)and (x2,y2) subtends at origin, prove that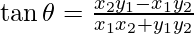 and
and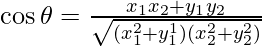
Solution:
Let the points A = (x1, y1), B = (x2, y2) and origin O = (0, 0)

Slopes of lines joining OA and OB are m1 = y1/x1 and m2 = y2/x2
Let θ be the angle between the lines OA and OB.
We know that,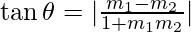
⇒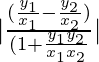
Therefore,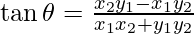
By the formula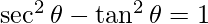 ,we get
,we get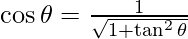
Substituting Tanθ from above equation, we get,
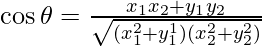
Therefore, hence proved.
Question 6: Prove that the straight lines(a+ b)x+(a – b)y=2ab, (a – b)x+(a + b)y=2ab and x + y=0 form an isosceles triangle whose vertical angle is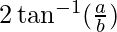
Solution:
Let m1, m2, m3 be the slopes of given lines respectively.
m1 =  , m2 =
, m2 = 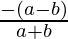 and m3 = -1
and m3 = -1
Let θ1, θ2, θ3 be the angles between the lines

Now,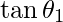 =
=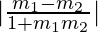
⇒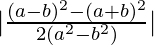
⇒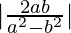 ⇒
⇒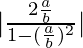
We know that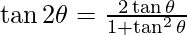 , using this above equation
, using this above equation
⇒ 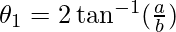
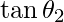 =
=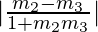
⇒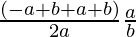
⇒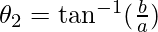
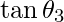 =
=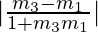
⇒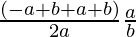
⇒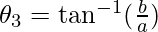
Here, angle θ2 and θ3 are equal, and θ1 is the vertical angle
Therefore, the given lines forms Isosceles triangle with vertical angle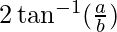
Question 7: Find the angle between the lines x = a, by + c = 0
Solution:
The given lines are in the form of x = constant and y=constant respectively
where x=c and y= -c/b
x = c line is parallel to y-axis as there is no y-coefficient
and 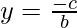 is parallel to x-axis as there is no x-coefficient
is parallel to x-axis as there is no x-coefficient

Therefore, the Angle between the two lines is 90°
Question 8: Find the tangent of the angle between the lines which have intercepts 3, 4, and 1, 8 on the axes respectively.
Solution:
Equation of line which have intercepts a, b on x and y-axis is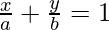
Therefore, the line with intercepts 3,4 is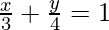
and the line with intercepts 1, 8 is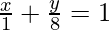
letm1 and m2 be the slopes of these lines,
m1 = 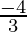 and m2 = -8
and m2 = -8
Now, let θ be the angle between the lines,
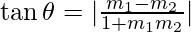
⇒ 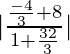
⇒ 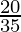 ⇒
⇒ 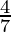
Therefore, The tangent of angle between the lines is 4/7
Question 9: Show that line a2x+ay+1 = 0 is perpendicular to line x-ay = 1
Solution:
Letm1 and m2 be the slopes of given lines,m1=-a andm2=1/a
Here, if we carefully observe,m1m2=-1 ,which means
From the formula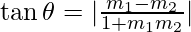 , denominator will become 0,
, denominator will become 0,
Therefore,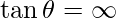 ,
, 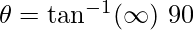 .
.
The angle between the two lines is 90°, and they are perpendicular to each other.
Therefore, Hence proved.
Question 10: Show that tangent of an angle between the lines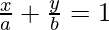 and
and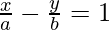 is
is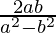 .
.
Solution:
Given lines,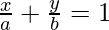 ⇒
⇒ 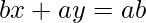
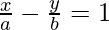 ⇒
⇒ 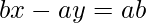
Let slopes of these lines arem1 andm2 respectively.
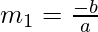 and
and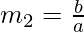
Now, let θ be the angle between the lines,
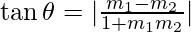
⇒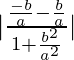
⇒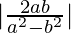
Therefore, Tangent of angle between the lines is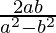
Hence, proved.
Share your thoughts in the comments
Please Login to comment...