Question 1(i). Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6
3x + 2y ≤ 6
x ≥ 0, y ≥ 0
Solution:
Let us convert the given inequations to equations.
2x + 3y = 6 -(1)
3x + 2y = 6 -(2)
x = 0 -(3)
y = 0 -(4)
Let us consider eq(1)
The line 2x + 3y = 6 meets the x-axis at (3, 0) and the y-axis at (0, 2).
And Origin(0, 0) satisfies the inequation 2x + 3y ≤ 6.
So, the section containing the origin will represent the solution set of inequation 2x + 3y ≤ 6.
Let us consider eq(2)
The line 3x + 2y = 6 meets the x-axis at (2, 0) and the y-axis at (0, 3).
And Origin(0, 0) satisfies the inequation 3x + 2y ≤ 6.
So, the section containing the origin will represent the solution set of inequation 3x + 2y ≤ 6.
x ≥ 0 and y ≥ 0 represent the first quadrant.
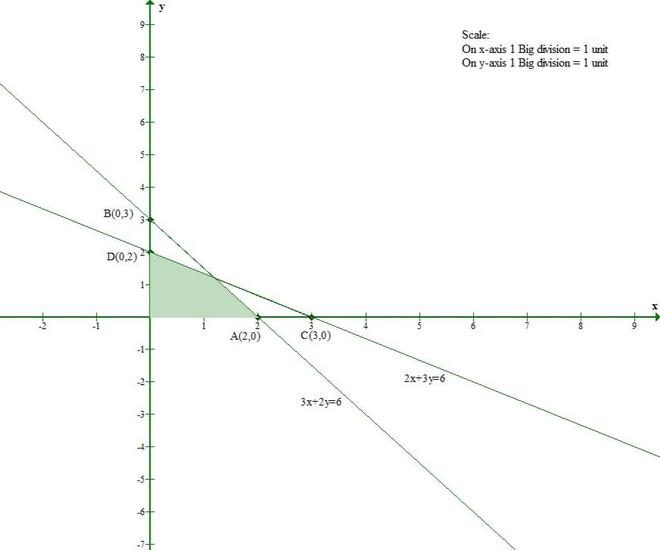
Thus, the shaded region represents the solution of the given inequations.
Question 1(ii). Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6
x + 4y ≤ 4
x ≥ 0, y ≥ 0
Solution:
Let us convert the given inequations to equations.
2x + 3y = 6 -(1)
x + 4y = 4 -(2)
x = 0 -(3)
y = 0 -(4)
Let us consider eq(1)
The line 2x + 3y = 6 meets the x-axis at (3, 0) and the y-axis at (0, 2).
And Origin(0, 0) satisfies the inequation 2x + 3y ≤ 6.
So, the section containing the origin will represent the solution set of inequation 2x + 3y ≤ 6.
Let us consider eq(2)
The line x + 4y = 4 meets the x-axis at (4, 0) and the y-axis at (0, 1).
And Origin(0, 0) satisfies the inequation x + 4y ≤ 4.
So, the section containing the origin will represent the solution set of inequation x + 4y ≤ 4.
x ≥ 0 and y ≥ 0 represent the first quadrant.
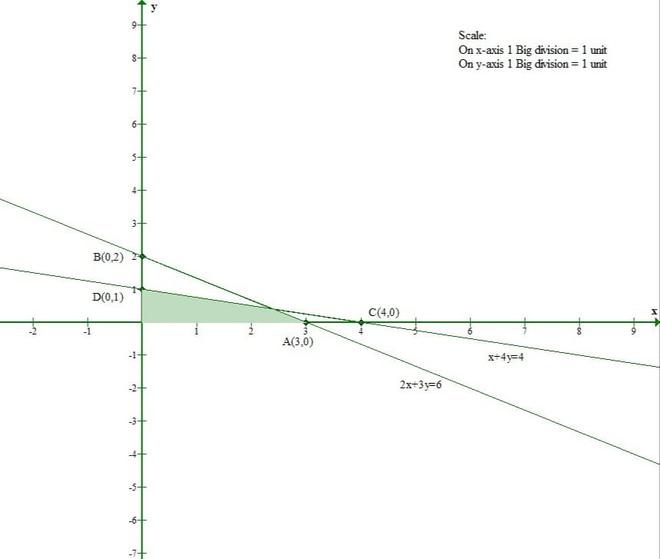
Thus, the shaded region represents the solution set of given inequations.
Question 1(iii). Solve the following systems of linear equation graphically:
x – y ≤ 1
x + 2y ≤ 8
2x + y ≥ 2
x ≥ 0, y ≥ 0
Solution:
Let us convert the given inequations to equations.
x – y = 1 – (1)
x + 2y = 8 -(2)
2x + y = 2 -(3)
x = 0, y = 0 -(4)
Let us consider eq(1)
The line x – y = 1 meets the x-axis at (1, 0) and the y-axis at (0, -1).
And Origin(0, 0) satisfies the inequation x – y ≤ 1
So, the section containing the origin will represent the solution set of inequation x – y ≤ 1.
Let us consider eq(2)
The line x + 2y = 8 meets the x-axis at (8, 0) and the y-axis at (0, 4).
And Origin(0, 0) satisfies the inequation x + 2y ≤ 8.
So, the section containing the origin will represent the solution set of inequation x + 2y ≤ 8.
Let us consider eq(3)
The line 2x + y = 2 meets the x-axis at (1, 0) and the y-axis at (0, 2).
And Origin(0, 0) doesnot satisfy the inequation 2x + y ≥ 2.
So, the section containing the origin will represent the solution set of inequation 2x + y ≥ 2.
x ≥ 0 and y ≥ 0 represent the first quadrant.
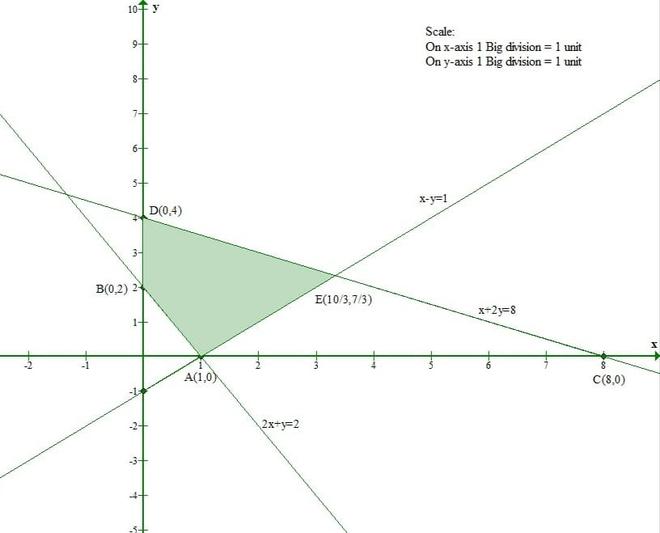
Thus the shaded region represents the solution set of given inequations.
Question 1(iv). Solve the following systems of linear equation graphically:
x + y ≥ 1
7x + 9y ≤ 63
x ≤ 6
y ≤ 5
x ≥ 0, y ≥ 0
Solution:
Let us convert the given inequations to equations.
x + y = 1 -(1)
7x + 9y = 63 -(2)
x = 6 -(3)
y = 5 -(4)
x = 0, y = 0
Let us consider eq(1)
The line x + y= 1 meets the x-axis at (1, 0) and the y-axis at (0, 1).
And Origin(0, 0) doesnot satisfy the inequation x + y ≥ 1.
So, the section containing the origin will represent the solution set of inequation x + y ≥ 1.
Let us consider eq(2)
The line 7x + 9y = 63 meets the x-axis at (9, 0) and the y-axis at (0, 7).
And Origin(0, 0) satisfies the inequation 7x + 9y ≤ 63.
So, the section containing the origin will represent the solution set of inequation 7x + 9y ≤ 63.
Let us consider eq(3)
The line x = 6 is parallel to y-axis and it is at a distance of 6 units from it.
And Origin(0, 0) satisfies the inequation x ≤ 6.
So, the section containing the origin will represent the solution set of inequation x ≤ 6.
Let us consider eq(4)
The line y = 5 is parallel to x-axis and it is at a distance of 5 units from it.
And Origin(0, 0) satisfies the inequation y ≤ 5.
So, the section containing the origin will represent the solution set of inequation y ≤ 5.
x ≥ 0 and y ≥ 0 represent the first quadrant.
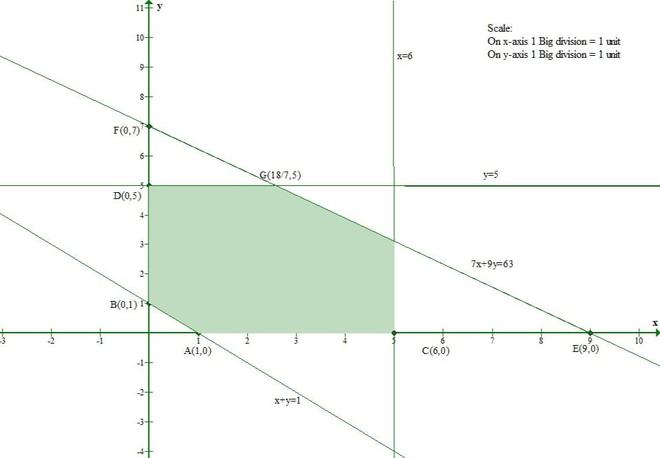
Thus, the shaded region represents the solution sets of given inequations.
Question 1(v). Solve the following systems of linear equation graphically:
2x + 3y ≤ 35
y ≥ 3
x ≥ 2
x ≥ 0, y ≥ 0
Solution:
Let us convert the given inequations to equations.
2x + 3y = 35 -(1)
y = 3 -(2)
x = 2 -(3)
x = 0, y = 0
Let us consider eq(1)
The line 2x + 3y = 35 meets the x-axis at (35/2, 0) and the y-axis at (0, 35/3).
And Origin(0, 0) satisfies the inequation 2x + 3y ≤ 35.
So, the section containing the origin will represent the solution set of inequation 2x + 3y ≤ 35.
Let us consider eq(2)
The line y = 3 is parallel to x-axis and it is at a distance of 3 units from it.
And Origin(0, 0) doesnot satisfy the inequation y ≥ 3.
So, the section containing the origin will represent the solution set of inequation y ≥ 3.
Let us consider eq(3)
The line x = 2 is parallel to y-axis and it is at a distance of 2 units from it.
And Origin(0, 0) doesnot satisfy the inequation x ≥ 2.
So, the section containing the origin will represent the solution set of inequation x ≥ 2.
x ≥ 0 and y ≥ 0 represent the first quadrant.
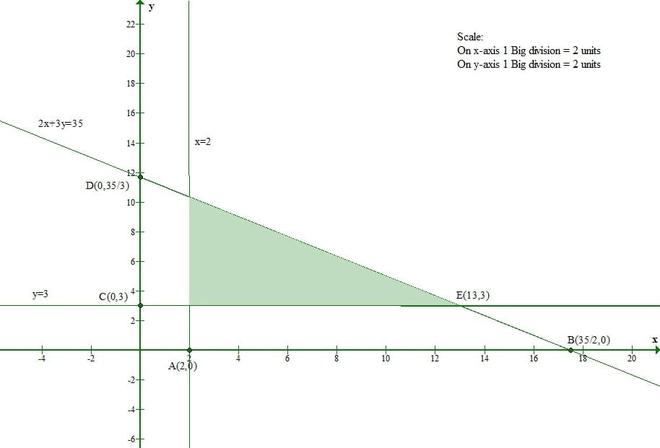
Thus, the shaded region represents the solution sets of given inequations.
Question 2(i). Show that the solution set of the following linear equations is empty set:
x – 2y ≥ 0
2x – y ≤ -2
x ≥ 0
y ≥ 0
Solution:
Let us convert the given inequations to equations.
x – 2y = 0 –(1)
2x – y = -2 -(2)
x = 0 -(3)
y = 0 -(4)
Let us consider eq(1)
The line x – 2y = 0 meets the x-axis at (0, 0) and the y-axis at (0, 0).
If x = 1 then y = 1/2
And Origin(0, 0) satisfies the inequation x – 2y ≥ 0.
So, the section containing the origin will represent the solution set of inequation x – 2y ≥ 0.
Let us consider eq(2)
The line 2x – y = -2 meets the x-axis at (-1, 0) and y-axis at (0, 2).
And Origin(0, 0) doesn’t satisfy the inequation 2x – y ≤ -2.
So, the section containing the origin will represent the solution set of inequation 2x – y ≤ -2.
Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.
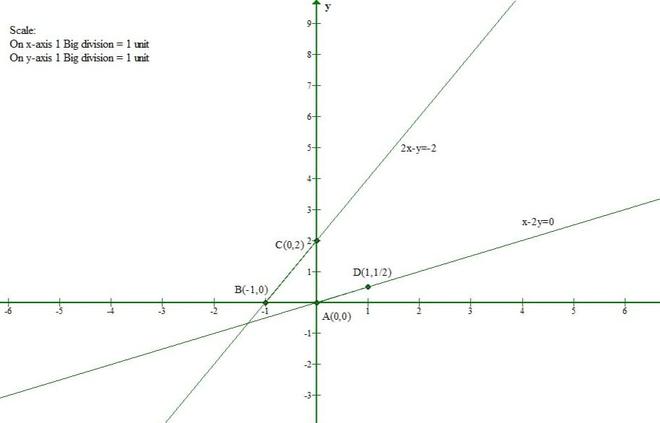
From the given graph we conclude that there is no common region in all the lines.
So, the solution set to given inequations is empty.
Hence Proved
Question 2(ii). Show that the solution set of the following linear equations is empty set:
x + 2y ≤ 3
3x + 4y ≥ 12
y ≥ 1
x ≥ 0
y ≥ 0
Solution:
Let us convert the given inequations to equations.
x + 2y = 3 -(1)
3x + 4y = 12 -(2)
y = 1 -(3)
x = 0 -(4)
y = 0 -(5)
Let us consider eq(1)
The line x + 2y = 3 meets the x-axis at (3, 0) and the y-axis at (0, 3/2).
And Origin(0, 0) satisfies the inequation x + 2y ≤ 3.
So, the section containing the origin will represent the solution set of inequation x + 2y ≤ 3.
Let us consider eq(2)
The line 3x + 4y = 12 meets the x-axis at (4, 0) and y-axis at (0, 3).
And Origin(0, 0) doesnot satisfy the inequation 3x + 4y ≥ 12.
So, the section containing the origin will represent the solution set of inequation 3x + 4y ≥ 12.
Let us consider eq(3)
The line y = 1 is parallel to x-axis and it is at a distance of 1 unit from it.
And Origin(0, 0) doesnot satisfy the inequation y ≥ 1.
So, the section containing the origin will represent the solution set of inequation y ≥ 1.
x ≥ 0 and y ≥ 0 represent the first quadrant.
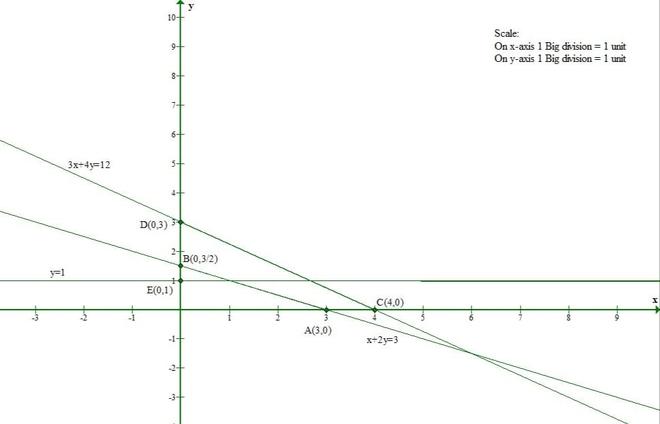
From the given graph we conclude that there is no common region in all the lines.
So, the solution set to given inequations is empty.
Hence Proved
Question 3. Find the linear inequations for which shaded region in the given below figure is the solution set. Draw the diagram for the solution set of linear inequations.
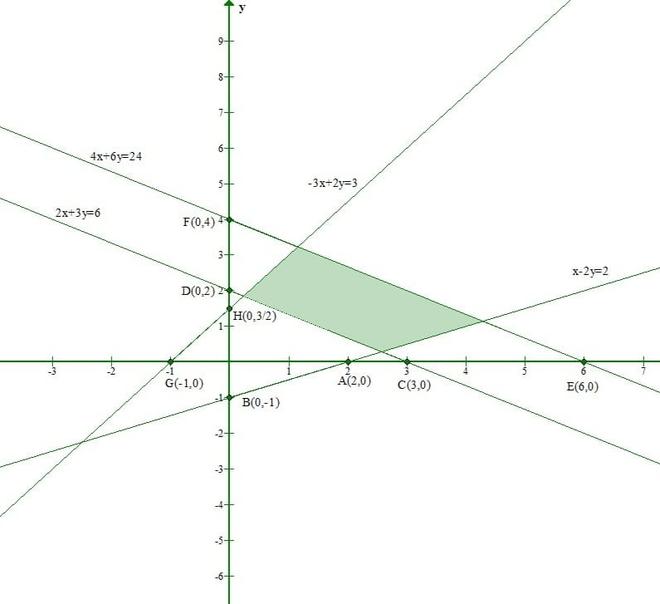
Solution:
Let us consider the line 2x + 3y = 6
The shaded region and origin(0, 0) are on the opposite side of this line.
And Origin(0, 0) doesnot satisfy the inequation 2x + 3y ≥ 6
Let us consider the line 4x + 6y = 24
The shaded region and origin (0, 0) are on the same side of this line.
And Origin(0, 0) satisfies the inequation 4x + 6y ≤ 24
Let us consider the line x – 2y = 2
The shaded region and origin (0, 0) are on the same side of this line.
And Origin(0, 0) satisfies the inequation x – 2y ≤ 2
Let us consider the line -3x + 2y = 3
The shaded region and origin (0, 0) are on the same side of this line.
And Origin(0, 0) satisfies the inequation -3x + 2y ≤ 3
Since the shaded part is in the first quadrant.
We also have to take x ≥ 0 and y ≥ 0.
Thus, the linear equations comprising the given solution set are:
2x + 3y ≥ 6, 4x + 6y ≤ 24, x – 2y ≤ 2, -3x + 2y ≤ 3, x ≥ 0 and y≥. 0.
Question 4. Find the linear inequations for which the solution set is the shaded region given below.
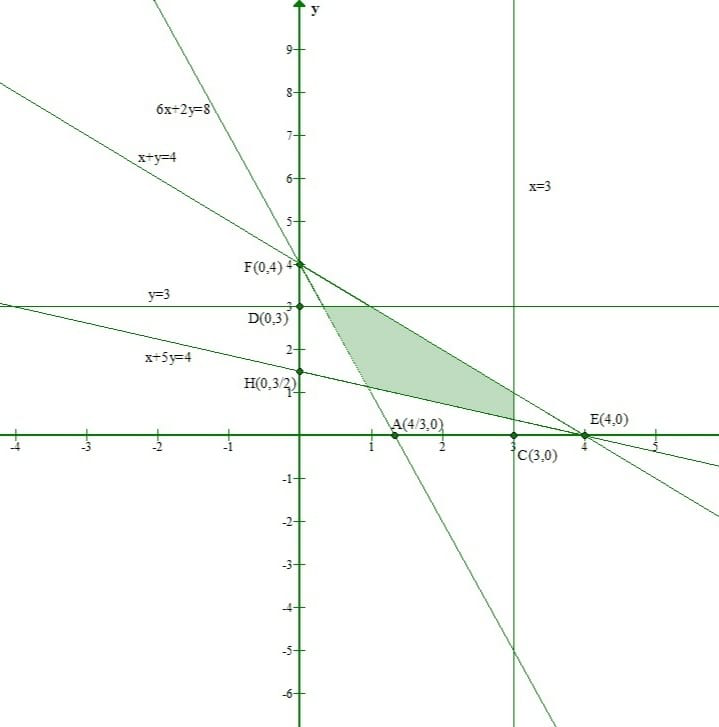
Solution:
Let us consider line x + y = 4
The shaded region and origin (0, 0) are on the same side of this line.
And Origin(0, 0) doesnot satisfy the inequation x + y ≤ 4
Let us consider line y = 3
The shaded region and origin (0, 0) are on the same side of this line.
And Origin(0, 0) satisfies the inequation y ≤ 3.
Let us consider line x = 3
The shaded region and origin (0, 0) are on the same side of this line.
And Origin(0, 0) satisfies the inequation x ≤ 3.
Let us consider line x + 5y = 4
The shaded region and origin (0, 0) are on the opposite side of this line.
And Origin(0, 0) doesnot satisfy the inequation x + 5y ≥ 4.
Let us consider line 6x + 2y = 8
The shaded region and origin (0, 0) are on the opposite side of this line.
And Origin(0, 0) doesnot satisfy the inequation 6x + 2y ≥ 8.
Since the shaded part is in the first quadrant.
We also have to take x ≥ 0 and y ≥ 0.
Thus, the linear equations comprising the given solution set are:
x + y ≤ 4, x ≤ 3, y ≤ 3 x + 5y ≥ 4, 6x + 2y ≥ 8, x ≥ 0 and y ≥ 0.
Question 5. Show that the solution set of the following linear inequations is an unbounded set:
x + y ≥ 9
3x + y ≥ 12
x ≥ 0 and y ≥ 0.
Solution:
Let us convert the given inequations to equations.
x + y = 9 -(1)
3x + y = 12 -(2)
x = 0 and y = 0 -(3)
Let us consider eq(1)
The line x + y = 9 meets the x-axis at (9, 0) and the y-axis at (0, 9).
And Origin(0, 0) doesnot satisfy the inequation x + y ≥ 9.
So, the section containing the origin will represent the solution set of inequation x + y ≥ 9.
Let us consider eq(2)
The line 3x + y = 12 meets the x-axis at (4, 0) and y-axis at (0, 12).
And Origin(0, 0) doesnot satisfy the inequation 3x + y ≥ 12.
So, the section containing the origin will represent the solution set of inequation 3x + y ≥ 12.
Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.
Hence, the solution set lies in the first quadrant.
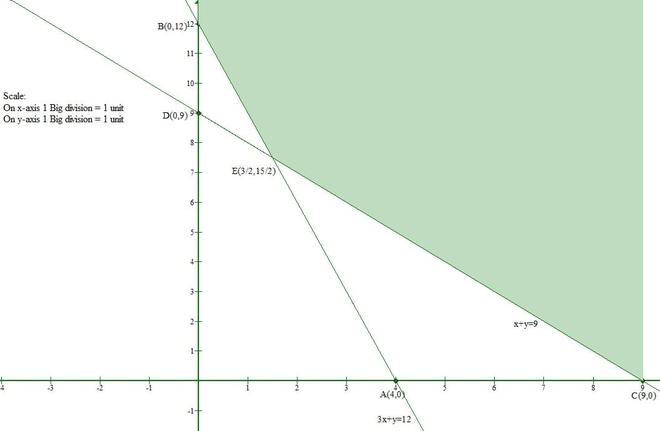
From the given graph we conclude that the shaded region is unbounded.
Hence, the solution set to the given set of inequalities is an unbounded set.
Question 6(i). Solve the following systems of inequations graphically:
2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6
Solution:
Let us convert the given inequations to equations.
2x + y = 8 -(1)
x + 2y = 8 -(2)
x + y = 6 -(3)
Let us consider eq(1)
The line 2x + y = 8 meets the x-axis at (4, 0) and the y-axis at (0, 8).
And Origin(0, 0) doesnot satisfy the inequation 2x + y ≥ 8.
So, the section containing the origin will represent the solution set of inequation 2x + y ≥ 8.
Let us consider eq(2)
The line x + 2y ≥ 8 meets the x-axis at (8, 0) and y-axis at (0, 4).
And Origin(0, 0) doesnot satisfy the inequation x + 2y ≥ 8.
So, the section containing the origin will represent the solution set of inequation x + 2y ≥ 8.
Let us consider eq(3)
The line x + y = 6 meets the x-axis at (6, 0) and the y-axis at (0, 6).
And Origin(0, 0) satisfies the inequation x + y ≤ 6.
So, the section containing the origin will represent the solution set of inequation x + y ≤ 6.
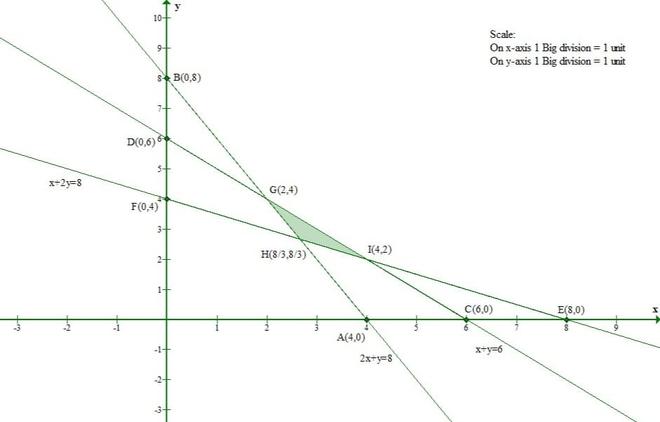
Hence, the solution set to the inequalities is the intersection of the above three solutions.
Thus, the shaded region represents the solution set of the given set of inequalities.
Question 6(ii). Solve the following systems of inequations graphically:
12x + 12y ≤ 840, 3x + 6y ≤ 300, 8x + 4y ≤ 480, x ≥ 0 and y ≥ 0.
Solution:
Let us convert the given inequations to equations.
12x + 12y = 840 -(1)
3x + 6y = 300 -(2)
8x + 4y = 480 -(3)
x = 0 and y = 0 -(4)
Let us consider eq(1)
The line 12x + 12y = 840 meets the x-axis at (70, 0) and the y-axis at (0, 70).
And Origin(0, 0) satisfies the inequation 12x + 12y ≤ 840.
So, the section containing the origin will represent the solution set of inequation 12x + 12y ≤ 840.
Let us consider eq(2)
The line 3x + 6y = 300 meets the x-axis at (100, 0) and the y-axis at (0, 50).
And Origin(0, 0) satisfies the inequation 3x + 6y ≤ 300.
So, the section containing the origin will represent the solution set of inequation 3x + 6y ≤ 300.
Let us consider eq(3)
The line 8x + 4y = 480 meets the x-axis at (60, 0) and the y-axis at (0, 120).
And Origin(0, 0) satisfies the inequation 8x + 4y ≤ 480.
So, the section containing the origin will represent the solution set of inequation 8x + 4y ≤ 480.
Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.
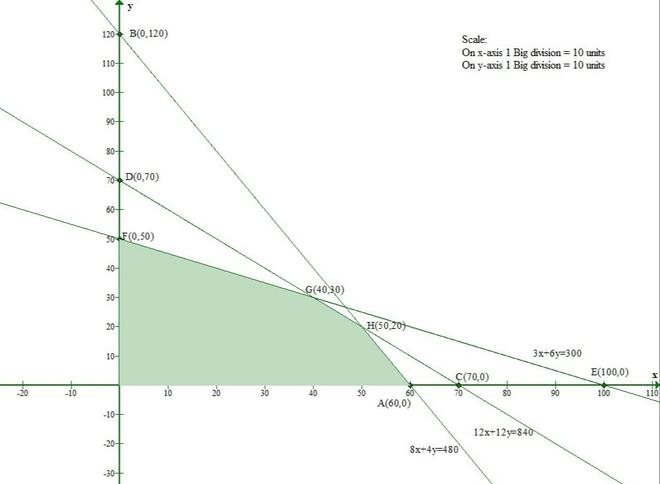
Hence, the solution set to the inequalities is the intersection of the above three solutions.
Thus, the shaded region represents the solution set of the given set of inequalities.
Question 6(iii). Solve the following systems of inequations graphically:
x + 2y ≤ 40, 3x + y ≥ 30, 4x + 3y ≥ 60, x ≥ 0 and y ≥ 0.
Solution:
Let us convert the given inequations to equations.
x + 2y = 40 -(1)
3x + y = 30 -(2)
4x + 3y = 60 -(3)
x = 0 and y = 0 -(4)
Let us consider eq(1)
The line x + 2y = 40 meets the x-axis at (40, 0) and the y-axis at (0, 20).
And Origin(0, 0) satisfies the inequation x + 2y ≤ 40.
So, the section containing the origin will represent the solution set of inequation x + 2y ≤ 40.
Let us consider eq(2)
The line 3x + y = 30 meets the x-axis at (10, 0) and y-axis at (0, 30).
And Origin(0, 0) doesnot satisfy the inequation 3x + y ≥ 30.
So, the section containing the origin will represent the solution set of inequation 3x + y ≥ 30.
Let us consider eq(3)
The line 4x + 3y = 60 meets the x-axis at (15, 0) and y-axis at (0, 20).
And Origin(0, 0) doesnot satisfy the inequation 4x + 3y ≥ 60.
So, the section containing the origin will represent the solution set of inequation4x + 3y ≥ 60.
Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.
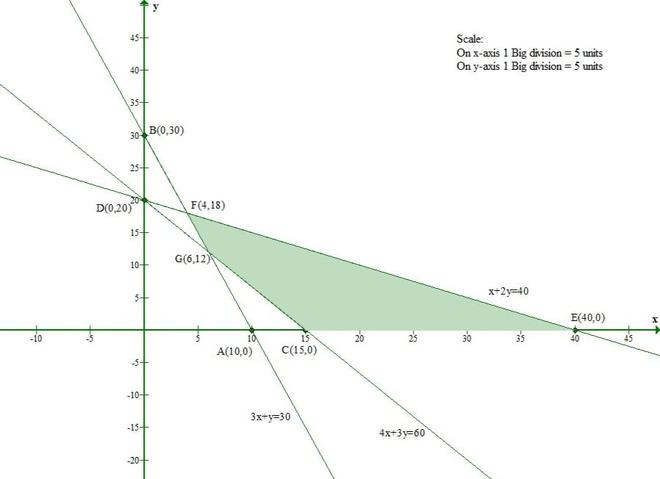
Hence, the solution set to the inequalities is the intersection of the above three solutions.
Thus, the shaded region represents the solution set of the given set of inequalities.
Question 6(iv) Solve the following systems of inequations graphically:
5x + y ≥ 10, 2x + 2y ≥ 12, x + 4y ≥ 12, x ≥ 0 and y ≥ 0.
Solution:
Let us convert the given inequations to equations.
5x + y = 10 -(1)
2x + 2y = 12 -(2)
x + 4y = 12 -(3)
x = 0 and y = 0 -(4)
Let us consider eq(1)
The line 5x + y = 10 meets the x-axis at (2, 0) and y-axis at (0, 10).
And Origin(0, 0) doesnot satisfy the inequation 5x + y ≥ 10.
So, the section containing the origin will represent the solution set of inequation 5x + y ≥ 10.
Let us consider eq(2)
The line 2x + 2y = 12 meets the x-axis at (6, 0) and y-axis at (0, 6).
And Origin(0, 0) doesnot satisfy the inequation 2x + 2y ≥ 12.
So, the section containing the origin will represent the solution set of inequation 2x + 2y ≥ 12.
Let us consider eq(3)
The line x + 4y = 12 meets the x-axis at (12, 0) and y-axis at (0, 3).
And Origin(0, 0) doesnot satisfy the inequation x + 4y ≥ 12.
So, the section containing the origin will represent the solution set of inequationx + 4y ≥ 12.
Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.
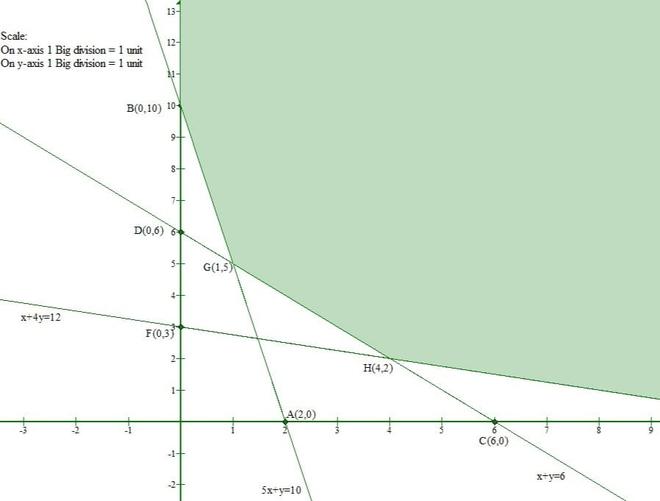
Hence, the solution set to the inequalities is the intersection of the above three solutions.
Thus, the shaded region represents the solution set of the given set of inequalities.
Question 7. Show that the following system of linear equations has no solutions
x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solution:
Let us convert the given inequations to equations.
x + 2y = 3 -(1)
3x + 4y = 12 -(2)
x = 0 and y = 1 -(3)
The points satisfying the eq(1) are
The points satisfying the eq(2) are
Now, let us draw the graph representing the given inequations
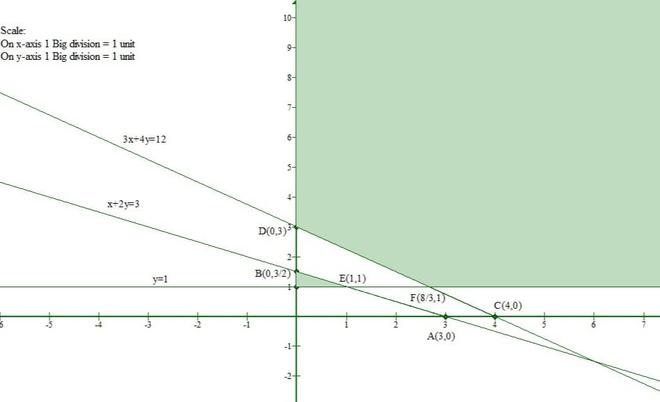
So, from the above graph we can observe that there is no common region.
Hence we can say that, the solution set of these inequalities has no solution.
Question 8. Show that the solution set of the following system of linear inequations is an unbounded region:
2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0
Solution:
Given that
2x + y ≥ 8 -(1)
x + 2y ≥ 10 -(2)
x ≥ 0 -(3)
y ≥ 0 -(4)
The points satisfying the line 2x + y = 8 are
The points satisfying the x + 2y = 10 are
Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.
Let us draw the graph representing the given inequations
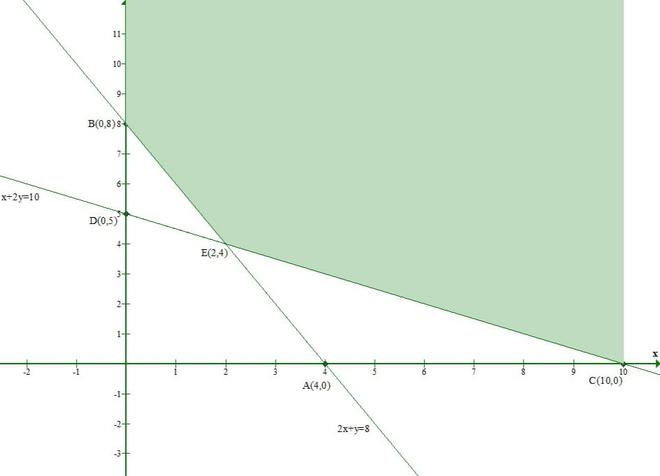
Since the common shaded region is the solution set of given set of inequalities.
Hence we proved that solution set of given linear inequations is an unbounded region.
Share your thoughts in the comments
Please Login to comment...