Class 11 RD Sharma Solutions – Chapter 15 Linear Inequations – Exercise 15.2 | Set 2
Last Updated :
25 Jan, 2021
Question 11. Solve each of the following system of equations in R: 4x – 1 ≤ 0, 3 – 4x < 0
Solution:
Let the first equation be 4x – 1 ≤ 0
⇒ 4x ≤ 1
⇒ x ≤ 1/4
and the second equation be 3 – 4x < 0
⇒ 4x > 3
⇒ x > 3/4
According to first equation, x lies in range ( -∞, 1/4 ] and according to second equation, x lies in range ( 3/4, -∞ )
Calculating the intersection of these two intervals we get no value for x. Therefore, given set of inequations has no solution.
Question 12. Solve each of the following system of equations in R: x + 5 > 2(x+1), 2 – x < 3(x+2)
Solution:
Let the first equation be x + 5 > 2(x+1)
⇒ x + 5 > 2x + 2
⇒ x < 3
and the second equation be 2 – x < 3(x+2)
⇒ 2 – x < 3x + 6
⇒ -4 < 4x
⇒ x > -1
Hence using above equations, we know x lies in range (-1,3)
Question 13. Solve each of the following system of equations in R: 2(x – 6) < 3x – 7, 11 – 2x < 6 – x
Solution:
Let the first equation be 2(x – 6) < 3x – 7
⇒ 2x – 12 < 3x – 7
⇒ -x < 5
⇒ x > -5
and the second equation be 11 – 2x < 6 – x
⇒ -x < -5
⇒ x > 5
Hence using above equations, we know x lies in range (5,∞)
Question 14. Solve each of the following system of equations in R: 5x – 7 < 3 (x + 3), 1 – 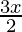 ≥ x – 4
≥ x – 4
Solution:
Let the first equation be 5x – 7 < 3 (x + 3)
⇒ 5x-7 < 3x + 9
⇒ 2x < 16
⇒ x < 8
and the second equation be1 –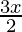 ≥ x – 4
≥ x – 4
⇒ x + 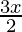 ≤ 5
≤ 5
⇒ 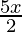 < 5
< 5
⇒ \frac{x}{2} ≤ 1
⇒ x ≤ 2
Hence using above equations, we know x lies in range [-∞, 2 ]
Question 15. Solve each of the following system of equations in R: 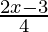 -2 ≥
-2 ≥ 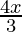 – 6, 2(2x + 3) < 6(x – 2) + 10
– 6, 2(2x + 3) < 6(x – 2) + 10
Solution:
Let the first equation be 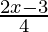 -2 ≥
-2 ≥ 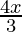 – 6
– 6
⇒ 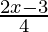 –
– 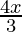 ≥ – 6 + 2
≥ – 6 + 2
⇒ 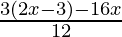 ≥ -4
≥ -4
⇒ 6x – 9 -16x ≥ -48
⇒ 10x ≤ 39
⇒ x ≤ 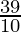
and the second equation be 2(2x + 3) < 6(x – 2) + 10
⇒ 4x + 6 < 6x -12 + 10
⇒ -2x < -8
⇒ x > 4
According to first equation, x lies in range ( -∞, 39/10 ] and according to second equation, x lies in range ( 4, ∞ )
Calculating the intersection of these two intervals we get no value for x. Therefore, given set of inequations has no solution.
Question 16. Solve each of the following system of equations in R: 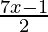 < -3,
< -3, 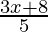 + 11 < 0
+ 11 < 0
Solution:
Let the first equation be 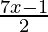 < -3
< -3
⇒ 7x – 1 < -6
⇒ 7x < -5
⇒ x < -5/7
and the second equation be 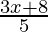 + 11 < 0
+ 11 < 0
⇒ 3x + 8 < -55
⇒ 3x < -63
⇒ x < -21
Hence using above equations, we know x lies in range ( -∞, -21)
Question 17. Solve each of the following system of equations in R: 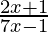 > 5,
> 5, 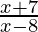 > 2
> 2
Solution:
Let the first equation be 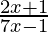 > 5
> 5
⇒ 2x + 1 > 5 (7x -1)
⇒ 2x – 35x > -6
⇒ – 33x > -6
⇒ x < 2/11
Also, 7x -1 > 0 ⇒ x > 1/7
using first equation we get, x lies in range 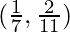
and let the second equation be 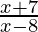 > 2
> 2
⇒ x + 7 > 2x – 16
⇒ 23 > x
⇒ x < 23
Also, x – 8 > 0 ⇒ x > 8
Hence using above equations, we know x lies in range ( 8, -23 )
Calculating the intersection of the two intervals we get after solving equation 1 and equation 2 we get no value for x. Therefore, given set of inequations has no solution.
Question 18. Solve each of the following system of equations in R: 0 < 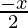 < 3
< 3
Solution:
Using the equation, 0 < 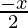 < 3
< 3
⇒ 0 < -x < 6
⇒ 0 > x > -6
⇒ x > -5
Hence using above equation, we know x lies in range ( -6, 0 )
Question 19. Solve each of the following system of equations in R: 10 ≤ -5 (x – 2) < 20
Solution:
Let the first equation be 10 ≤ -5 (x – 2) < 20
⇒ 10 ≤ -5x + 10 < 20
⇒ 0 ≤ -5x < 10
⇒ 0 ≤ x < -2
Hence using above equations, we know x lies in range ( -2, 0 ]
Question 20. Solve each of the following system of equations in R: -5 < 2x -3 < 5
Solution:
Using the equation -5 < 2x -3 < 5
⇒ -2 < 2x < 8
⇒ -1 < x < 4
Hence using above equations, we know x lies in range ( -1, 4 )
Question 21. Solve each of the following system of equations in R: 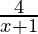 ≤ 3 ≤
≤ 3 ≤ 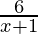 , x>0
, x>0
Solution:
Using the equation 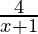 ≤ 3 ≤
≤ 3 ≤ 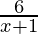 , x>0
, x>0
⇒ 4 ≤ 3 (x+1) ≤ 6
⇒ 4 ≤ 3x + 3 ≤ 6
⇒ 4 ≤ 3x + 3 ≤ 6
⇒ 1 ≤ 3x ≤ 3
⇒ 1/3 ≤ x ≤ 1
Hence using above equations, we know x lies in range ![Rendered by QuickLaTeX.com \left [ \frac{1}{3}, 1 \right ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-56bde869128e832ebbd8c27843732bdd_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...