Class 11 RD Sharma Solutions – Chapter 30 Derivatives – Exercise 30.4 | Set 1
Last Updated :
16 May, 2021
Question 1. Differentiate x3 sin x with respect to x.
Solution:
We have,
=> y = x3 sin x
On differentiating both sides with respect to x, we get,
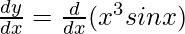
On using product rule, we get,
= 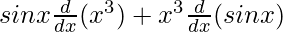
= sinx (3x2) + x3 (cosx)
= 3x2 sinx + x3 cosx
= x2 (3 sinx + x cos x)
Question 2. Differentiate x3 ex with respect to x.
Solution:
We have,
=> y = x3 ex
On differentiating both sides with respect to x, we get,
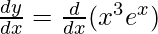
On using product rule, we get,
= 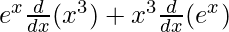
= ex (3x2) + x3 (ex)
= 3x2 ex + x3 ex
= x2 ex (3 + x)
Question 3. Differentiate x2 ex log x with respect to x.
Solution:
We have,
=> y = x2 ex log x
On differentiating both sides with respect to x, we get,
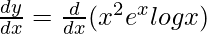
On using product rule, we get,
= 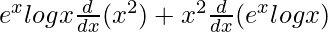
On using product rule again in the second part of the expression, we get,
= ![Rendered by QuickLaTeX.com e^xlogx(2x)+x^2[logx\frac{d}{dx}(e^x)+e^x\frac{d}{dx}(logx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-50f468ac269188f4a02ceea30d3e0f5b_l3.png)
= 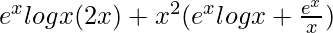
= 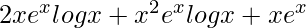
= 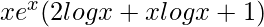
Question 4. Differentiate xn tan x with respect to x.
Solution:
We have,
=> y = xn tan x
On differentiating both sides with respect to x, we get,
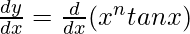
On using product rule, we get,
= 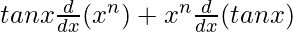
= 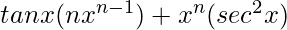
= 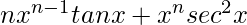
= 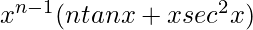
Question 5. Differentiate xn loga x with respect to x.
Solution:
We have,
=> y = xn loga x
On differentiating both sides with respect to x, we get,
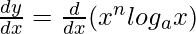
On using product rule, we get,
= 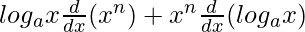
= 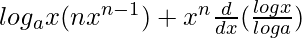
= 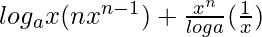
= 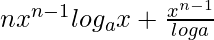
= 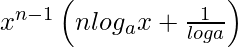
Question 6. Differentiate (x3+x2+1)sinx with respect to x.
Solution:
We have,
=> y = 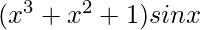
On differentiating both sides with respect to x, we get,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[(x^3+x^2+1)sinx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5f8a0cfe5d3cbda499e0e5c636a7a93d_l3.png)
On using product rule, we get,
= 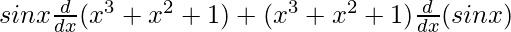
= 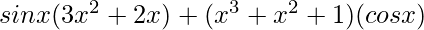
= 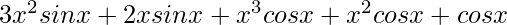
Question 7. Differentiate sin x cos x with respect to x.
Solution:
We have,
=> y = sin x cos x
On differentiating both sides with respect to x, we get,
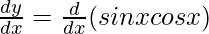
On using product rule, we get,
= 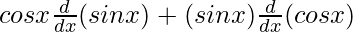
= cos x (cos x) − sin x (−sin x)
= cos2 x − sin2 x
= cos2 x − (1 − cos2 x)
= cos2 x − 1 + cos2 x
= 2 cos2 x − 1
= cos 2x
Question 8. Differentiate 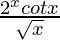 with respect to x.
with respect to x.
Solution:
We have,
=> y = 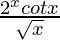
=> y = 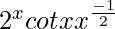
On differentiating both sides with respect to x, we get,
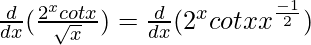
On using product rule, we get,
= 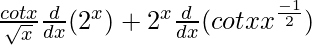
On using product rule again in the second part of the expression, we get,
= ![Rendered by QuickLaTeX.com \frac{2^xlog2cotx}{\sqrt{x}}+2^x[x^{\frac{-1}{2}}\frac{d}{dx}(cotx)+cotx\frac{d}{dx}(x^{\frac{-1}{2}})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1c81227965ff83f53d695ff48c03e5d2_l3.png)
= ![Rendered by QuickLaTeX.com \frac{2^xlog2cotx}{\sqrt{x}}+2^x\left[\frac{-cosec^2x}{\sqrt{x}}+\frac{-cotx}{2}\frac{1}{x^{\frac{3}{2}}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6db236716844c0b880d8e16632765e89_l3.png)
= 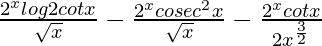
= 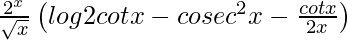
Question 9. Differentiate x2 sin x log x with respect to x.
Solution:
We have,
=> y = x2 sin x log x
On differentiating both sides with respect to x, we get,
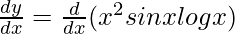
On using product rule, we get,
= 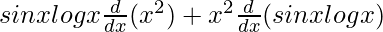
On using product rule again in the second part of the expression, we get,
= ![Rendered by QuickLaTeX.com sinxlogx(2x)+x^2[logx\frac{d}{dx}(sinx)+sinx\frac{d}{dx}(logx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-76f342a587bec6657c8eefdcea33397c_l3.png)
= ![Rendered by QuickLaTeX.com 2xsinxlogx+x^2[logxcosx+sinx(\frac{1}{x})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ed845be26a8ad891d95f2e321d992dd1_l3.png)
= 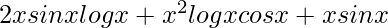
Question 10. Differentiate x5 ex + x6 log x with respect to x.
Solution:
We have,
=> y = x5 ex + x6 log x
On differentiating both sides with respect to x, we get,
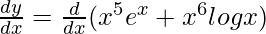
On using chain rule, we get,
= 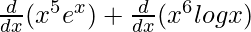
On using product rule, we get,
= 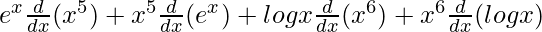
= 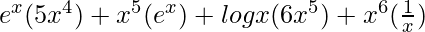
= 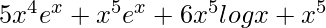
= 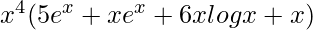
Share your thoughts in the comments
Please Login to comment...