Iterated Logarithm log*(n)
Last Updated :
19 Aug, 2022
Iterated Logarithm or Log*(n) is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1.
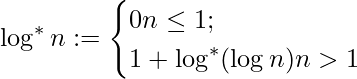
Applications: It is used in the analysis of algorithms (Refer Wiki for details)
C++
#include <bits/stdc++.h>
using namespace std;
int _log(double x, double base)
{
return (int)(log(x) / log(base));
}
double recursiveLogStar(double n, double b)
{
if (n > 1.0)
return 1.0 + recursiveLogStar(_log(n, b), b);
else
return 0;
}
int main()
{
int n = 100, base = 5;
cout << "Log*(" << n << ") = "
<< recursiveLogStar(n, base) << "\n";
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int _log(double x,
double base)
{
return (int)(Math.log(x) /
Math.log(base));
}
static double recursiveLogStar(double n,
double b)
{
if (n > 1.0)
return 1.0 +
recursiveLogStar(_log(n,
b), b);
else
return 0;
}
public static void main (String[] args)
{
int n = 100, base = 5;
System.out.println("Log*(" + n + ") = " +
recursiveLogStar(n, base));
}
}
|
Python3
import math
def _log(x, base):
return (int)(math.log(x) / math.log(base))
def recursiveLogStar(n, b):
if(n > 1.0):
return 1.0 + recursiveLogStar(_log(n, b), b)
else:
return 0
if __name__=='__main__':
n = 100
base = 5
print("Log*(", n, ") = ", recursiveLogStar(n, base))
|
C#
using System;
public class GFG{
static int _log(double x, double baset)
{
return (int)(Math.Log(x) /
Math.Log(baset));
}
static double recursiveLogStar(double n,
double b)
{
if (n > 1.0)
return 1.0 +
recursiveLogStar(_log(n,
b), b);
else
return 0;
}
static public void Main (){
int n = 100, baset = 5;
Console.WriteLine("Log*(" + n + ") = " +
recursiveLogStar(n, baset));
}
}
|
PHP
<?php
function _log($x, $base)
{
return (int)(log($x) / log($base));
}
function recursiveLogStar($n, $b)
{
if ($n > 1.0)
return 1.0 +
recursiveLogStar(_log($n,
$b), $b);
else
return 0;
}
$n = 100; $base = 5;
echo "Log*(" , $n , ")"," = ",
recursiveLogStar($n, $base), "\n";
?>
|
Javascript
<script>
function _log( x, base)
{
return (Math.log(x) /
Math.log(base));
}
function recursiveLogStar(n, b)
{
if (n > 1.0)
return 1.0 +
recursiveLogStar(_log(n,
b), b);
else
return 0;
}
let n = 100, base = 5;
document.write("Log*(" + n + ") = " +
recursiveLogStar(n, base));
</script>
|
Output :
Log*(100) = 2
Time Complexity: O(logn)
Auxiliary Space: O(logn) due to recursive stack space
Iterative Implementation :
C++
int iterativeLogStar(double n, double b)
{
int count = 0;
while (n >= 1) {
n = _log(n, b);
count++;
}
return count;
}
|
Java
public static int iterativeLogStar(double n, double b)
{
int count = 0;
while (n >= 1) {
n = _log(n, b);
count++;
}
return count;
}
|
Python3
def iterativeLogStar(n, b):
count = 0
while(n >= 1):
n = _log(n, b)
count = count + 1
return count
|
C#
static int iterativeLogStar(double n, double b)
{
int count = 0;
while (n >= 1)
{
n = _log(n, b);
count++;
}
return count;
}
|
Javascript
<script>
function iterativeLogStar(n, b)
{
var count = 0;
while (n >= 1)
{
n = _log(n, b);
count++;
}
return count;
}
</script>
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...