Juggler Sequence

Juggler Sequence is a series of integer number in which the first term starts with a positive integer number a and the remaining terms are generated from the immediate previous term using the below recurrence relation : 

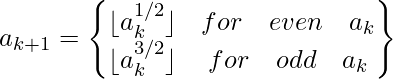
Juggler Sequence starting with number 3: 
3, 5, 11, 36, 6, 2, 1
Juggler Sequence starting with number 9: 
9, 27, 140, 11, 36, 6, 2, 1
Given a number n we have to print the Juggler Sequence for this number as the first term of the sequence. 
Examples: 

Input: 9
Output: 9, 27, 140, 11, 36, 6, 2, 1
We start with 9 and use above formula to get
next terms.

Input: 6
Output: 6, 2, 1

C++

// C++ implementation of Juggler Sequence
#include <bits/stdc++.h>
using namespace std;

// This function prints the juggler Sequence
void printJuggler(long long n)
{
    long long a = n;

    // print the first term
    cout << a << " ";

    // calculate terms until
    // last term is not 1
    while (a != 1)
    {
        long long b = 0;

        // Check if previous term
        // is even or odd
        if (a % 2 == 0)

            // calculate next term
            b = floor(sqrt(a));

        else

            // for odd previous term
            // calculate next term
            b = floor(sqrt(a) *
                      sqrt(a) * sqrt(a));

        cout << b << " ";
        a = b;
    }
}

// Driver Code
int main()
{
    printJuggler(37);
    cout <<"\n";
    printJuggler(9);
    return 0;
}

// This code is contributed by shubhamsingh10

C

// C implementation of Juggler Sequence
#include<stdio.h>
#include<math.h>

// This function prints the juggler Sequence
void printJuggler(int n)
{
    int a = n;

    // print the first term
    printf("%d ", a);

    // calculate terms until last term is not 1
    while (a != 1)
    {
        int b = 0;

        // Check if previous term is even or odd
        if (a%2 == 0)

            // calculate next term
            b  = floor(sqrt(a));

        else

            // for odd previous term calculate
            // next term
            b = floor(sqrt(a)*sqrt(a)*sqrt(a));

        printf("%d ", b);
        a = b;
    }
}

//driver program to test above function
int main()
{
    printJuggler(3);
    printf("\n");
    printJuggler(9);
    return 0;
}

Java

// Java implementation of Juggler Sequence
import java.io.*;
import java.math.*;

class GFG {

    // This function prints the juggler Sequence
    static void printJuggler(int n)
    {
        int a = n;

       // print the first term
       System.out.print(a+" ");

      // calculate terms until last term is not 1
       while (a != 1)
       {
          int b = 0;

          // Check if previous term is even or odd
          if (a%2 == 0)

             // calculate next term
                b  = (int)Math.floor(Math.sqrt(a));

          else

            // for odd previous term calculate
            // next term
                b =(int) Math.floor(Math.sqrt(a) *
                               Math.sqrt(a) * Math.sqrt(a));

          System.out.print( b+" ");
          a = b;
        }
    }

// Driver program to test above function
public static void main (String[] args) {
    printJuggler(3);
    System.out.println();
    printJuggler(9);
    }
}

//This code is contributed by Nikita Tiwari.

Python3

import math

#This function prints the juggler Sequence
def printJuggler(n) :
    a = n

    # print the first term
    print (a,end=" ")

    # calculate terms until last term is not 1
    while (a != 1) :
        b = 0

        # Check if previous term is even or odd
        if (a%2 == 0) :

            # calculate next term
            b  = (int)(math.floor(math.sqrt(a)))

        else :
            # for odd previous term calculate
            # next term
            b = (int) (math.floor(math.sqrt(a)*math.sqrt(a)*
                                         math.sqrt(a)))

        print (b,end=" ")
        a = b

printJuggler(3)
print()
printJuggler(9)

# This code is contributed by Nikita Tiwari.

C#

// C# implementation of Juggler Sequence
using System;

class GFG {

    // This function prints the juggler Sequence
    static void printJuggler(int n)
    {
        int a = n;

    // print the first term
    Console.Write(a+" ");

    // calculate terms until last term is not 1
    while (a != 1)
    {
        int b = 0;

        // Check if previous term is even or odd
        if (a%2 == 0)

            // calculate next term
                b = (int)Math.Floor(Math.Sqrt(a));

        else

            // for odd previous term calculate
            // next term
                b =(int) Math.Floor(Math.Sqrt(a) *
                     Math.Sqrt(a) * Math.Sqrt(a));

        Console.Write( b+" ");
        a = b;
        }
    }

// Driver Code
public static void Main () {
    printJuggler(3);
    Console.WriteLine();
    printJuggler(9);
    }
}

// This code is contributed by Nitin Mittal

PHP

<?php
// PHP implementation of
// Juggler Sequence

// function prints the
// juggler Sequence
function printJuggler($n)
{
    $a = $n;

    // print the first term
    echo($a . " ");

    // calculate terms until
    // last term is not 1
    while ($a != 1)
    {
        $b = 0;

        // Check if previous
        // term is even or odd
        if ($a % 2 == 0)

            // calculate next term
            $b = floor(sqrt($a));

        else

            // for odd previous term
            // calculate next term
            $b = floor(sqrt($a) * sqrt($a) *
                                  sqrt($a));

        echo($b . " ");
        $a = $b;
    }
}

// Driver Code
printJuggler(3);
echo("\n");
printJuggler(9);

// This code is contributed by Ajit.
?>

Javascript

<script>

// Javascript implementation of Juggler Sequence

    // This function prints the juggler Sequence
    function printJuggler(n)
    {
        let a = n;

       // print the first term
       document.write(a+" ");

      // calculate terms until last term is not 1
       while (a != 1)
       {
          let b = 0;

          // Check if previous term is even or odd
          if (a%2 == 0)

             // calculate next term
                b  = Math.floor(Math.sqrt(a));

          else

            // for odd previous term calculate
            // next term
                b = Math.floor(Math.sqrt(a) *
                               Math.sqrt(a) * Math.sqrt(a));

          document.write( b+" ");
          a = b;
        }
    }

// Driver code to test above methods

    printJuggler(3);
    document.write("<br/>");
    printJuggler(9);

 // This code is contributed by avijitmondal1998.
</script>

Output: 

3 5 11 36 6 2 1 
9 27 140 11 36 6 2 1

Time complexity: O(nlogn) since using a single while loop and finding square root takes logarithmic time.

Space complexity: O(1) for constant variables

Important Points:

• The terms in Juggler Sequence first increase to a peak value and then start decreasing.
• The last term in Juggler Sequence is always 1.

Reference:
https://en.wikipedia.org/wiki/Juggler_sequence
If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.