LCM of given array elements

Given an array of n numbers, find the LCM of it. 

 Example:

Input : {1, 2, 8, 3}
Output : 24

Input : {2, 7, 3, 9, 4}
Output : 252

Method 1 :

We know,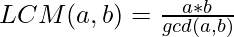 
The above relation only holds for two numbers, 

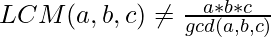
The idea here is to extend our relation for more than 2 numbers. Let’s say we have an array arr[] that contains n elements whose LCM needed to be calculated.

The main steps of our algorithm are: 

1. Initialize ans = arr[0].
2. Iterate over all the elements of the array i.e. from i = 1 to i = n-1 
   At the ith iteration ans = LCM(arr[0], arr[1], …….., arr[i-1]). This can be done easily as LCM(arr[0], arr[1], …., arr[i]) = LCM(ans, arr[i]). Thus at i’th iteration we just have to do ans = LCM(ans, arr[i]) = ans x arr[i] / gcd(ans, arr[i])
   

Below is the implementation of the above algorithm : 

C++

// C++ program to find LCM of n elements
#include <bits/stdc++.h>
using namespace std;

typedef long long int ll;

// Utility function to find
// GCD of 'a' and 'b'
int gcd(int a, int b)
{
    if (b == 0)
        return a;
    return gcd(b, a % b);
}

// Returns LCM of array elements
ll findlcm(int arr[], int n)
{
    // Initialize result
    ll ans = arr[0];

    // ans contains LCM of arr[0], ..arr[i]
    // after i'th iteration,
    for (int i = 1; i < n; i++)
        ans = (((arr[i] * ans)) /
                (gcd(arr[i], ans)));

    return ans;
}

// Driver Code
int main()
{
    int arr[] = { 2, 7, 3, 9, 4 };
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("%lld", findlcm(arr, n));
    return 0;
}

Java

// Java Program to find LCM of n elements
import java.io.*;

public class GFG {

    public static long lcm_of_array_elements(int[] element_array)
    {
        long lcm_of_array_elements = 1;
        int divisor = 2;

        while (true) {
            int counter = 0;
            boolean divisible = false;

            for (int i = 0; i < element_array.length; i++) {

                // lcm_of_array_elements (n1, n2, ... 0) = 0.
                // For negative number we convert into
                // positive and calculate lcm_of_array_elements.

                if (element_array[i] == 0) {
                    return 0;
                }
                else if (element_array[i] < 0) {
                    element_array[i] = element_array[i] * (-1);
                }
                if (element_array[i] == 1) {
                    counter++;
                }

                // Divide element_array by devisor if complete
                // division i.e. without remainder then replace
                // number with quotient; used for find next factor
                if (element_array[i] % divisor == 0) {
                    divisible = true;
                    element_array[i] = element_array[i] / divisor;
                }
            }

            // If divisor able to completely divide any number
            // from array multiply with lcm_of_array_elements
            // and store into lcm_of_array_elements and continue
            // to same divisor for next factor finding.
            // else increment divisor
            if (divisible) {
                lcm_of_array_elements = lcm_of_array_elements * divisor;
            }
            else {
                divisor++;
            }

            // Check if all element_array is 1 indicate
            // we found all factors and terminate while loop.
            if (counter == element_array.length) {
                return lcm_of_array_elements;
            }
        }
    }

    // Driver Code
    public static void main(String[] args)
    {
        int[] element_array = { 2, 7, 3, 9, 4 };
        System.out.println(lcm_of_array_elements(element_array));
    }
}

// Code contributed by Mohit Gupta_OMG

Python

# Python Program to find LCM of n elements

def find_lcm(num1, num2):
    if(num1>num2):
        num = num1
        den = num2
    else:
        num = num2
        den = num1
    rem = num % den
    while(rem != 0):
        num = den
        den = rem
        rem = num % den
    gcd = den
    lcm = int(int(num1 * num2)/int(gcd))
    return lcm

l = [2, 7, 3, 9, 4]

num1 = l[0]
num2 = l[1]
lcm = find_lcm(num1, num2)

for i in range(2, len(l)):
    lcm = find_lcm(lcm, l[i])

print(lcm)

# Code contributed by Mohit Gupta_OMG

C#

// C# Program to find LCM of n elements
using System;

public class GFG {

    public static long lcm_of_array_elements(int[] element_array)
    {
        long lcm_of_array_elements = 1;
        int divisor = 2;

        while (true) {

            int counter = 0;
            bool divisible = false;
            for (int i = 0; i < element_array.Length; i++) {

                // lcm_of_array_elements (n1, n2, ... 0) = 0.
                // For negative number we convert into
                // positive and calculate lcm_of_array_elements.
                if (element_array[i] == 0) {
                    return 0;
                }
                else if (element_array[i] < 0) {
                    element_array[i] = element_array[i] * (-1);
                }
                if (element_array[i] == 1) {
                    counter++;
                }

                // Divide element_array by devisor if complete
                // division i.e. without remainder then replace
                // number with quotient; used for find next factor
                if (element_array[i] % divisor == 0) {
                    divisible = true;
                    element_array[i] = element_array[i] / divisor;
                }
            }

            // If divisor able to completely divide any number
            // from array multiply with lcm_of_array_elements
            // and store into lcm_of_array_elements and continue
            // to same divisor for next factor finding.
            // else increment divisor
            if (divisible) {
                lcm_of_array_elements = lcm_of_array_elements * divisor;
            }
            else {
                divisor++;
            }

            // Check if all element_array is 1 indicate
            // we found all factors and terminate while loop.
            if (counter == element_array.Length) {
                return lcm_of_array_elements;
            }
        }
    }

    // Driver Code
    public static void Main()
    {
        int[] element_array = { 2, 7, 3, 9, 4 };
        Console.Write(lcm_of_array_elements(element_array));
    }
}

// This Code is contributed by nitin mittal

PHP

<?php
// PHP program to find LCM of n elements

// Utility function to find
// GCD of 'a' and 'b'
function gcd($a, $b)
{
    if ($b == 0)
        return $a;
    return gcd($b, $a % $b);
}

// Returns LCM of array elements
function findlcm($arr, $n)
{

    // Initialize result
    $ans = $arr[0];

    // ans contains LCM of
    // arr[0], ..arr[i]
    // after i'th iteration,
    for ($i = 1; $i < $n; $i++)
        $ans = ((($arr[$i] * $ans)) /
                (gcd($arr[$i], $ans)));

    return $ans;
}

// Driver Code
$arr = array(2, 7, 3, 9, 4 );
$n = sizeof($arr);
echo findlcm($arr, $n);

// This code is contributed by ChitraNayal
?>

Javascript

<script>

// Javascript program to find LCM of n elements

// Utility function to find
// GCD of 'a' and 'b'
function gcd(a, b)
{
    if (b == 0)
        return a;
    return gcd(b, a % b);
}

// Returns LCM of array elements
function findlcm(arr, n)
{
    // Initialize result
    let ans = arr[0];

    // ans contains LCM of arr[0], ..arr[i]
    // after i'th iteration,
    for (let i = 1; i < n; i++)
        ans = (((arr[i] * ans)) /
                (gcd(arr[i], ans)));

    return ans;
}

// Driver Code

    let arr = [ 2, 7, 3, 9, 4 ];
    let n = arr.length;
    document.write(findlcm(arr, n));

// This code is contributed by Mayank Tyagi

</script>

Output

252

Time Complexity: O(n * log(min(a, b))), where n represents the size of the given array.
Auxiliary Space: O(n*log(min(a, b))) due to recursive stack space.

Below is the implementation of the above algorithm Recursively :

C++

#include <bits/stdc++.h>
using namespace std;

//recursive implementation
int LcmOfArray(vector<int> arr, int idx){
    // lcm(a,b) = (a*b/gcd(a,b))
    if (idx == arr.size()-1){
        return arr[idx];
    }
    int a = arr[idx];
    int b = LcmOfArray(arr, idx+1);
    return (a*b/__gcd(a,b)); // __gcd(a,b) is inbuilt library function
}


int main() {

    vector<int> arr = {1,2,8,3};
    cout << LcmOfArray(arr, 0) << "\n";
      arr = {2,7,3,9,4};
      cout << LcmOfArray(arr,0) << "\n";
    return 0;
}

Java

import java.util.*;
import java.io.*;

class GFG
{

  // Recursive function to return gcd of a and b
  static int __gcd(int a, int b)
  {
    return b == 0? a:__gcd(b, a % b);
  }

  // recursive implementation
  static int LcmOfArray(int[] arr, int idx)
  {

    // lcm(a,b) = (a*b/gcd(a,b))
    if (idx == arr.length - 1){
      return arr[idx];
    }
    int a = arr[idx];
    int b = LcmOfArray(arr, idx+1);
    return (a*b/__gcd(a,b)); //
  }


  public static void main(String[] args)
  {

    int[] arr = {1,2,8,3};
    System.out.print(LcmOfArray(arr, 0)+ "\n");
    int[]  arr1 = {2,7,3,9,4};
    System.out.print(LcmOfArray(arr1,0)+ "\n");
  }
}

// This code is contributed by gauravrajput1

Python3

def __gcd(a, b):
    if (a == 0):
        return b
    return __gcd(b % a, a)

# recursive implementation
def LcmOfArray(arr, idx):

    # lcm(a,b) = (a*b/gcd(a,b))
    if (idx == len(arr)-1):
        return arr[idx]
    a = arr[idx]
    b = LcmOfArray(arr, idx+1)
    return int(a*b/__gcd(a,b)) # __gcd(a,b) is inbuilt library function

arr = [1,2,8,3]
print(LcmOfArray(arr, 0))
arr = [2,7,3,9,4]
print(LcmOfArray(arr,0))

# This code is contributed by divyeshrabadiya07.

C#

using System;
class GFG {

    // Function to return
    // gcd of a and b
    static int __gcd(int a, int b)
    {
        if (a == 0)
            return b;
        return __gcd(b % a, a);
    }

    //recursive implementation
    static int LcmOfArray(int[] arr, int idx){
        // lcm(a,b) = (a*b/gcd(a,b))
        if (idx == arr.Length-1){
            return arr[idx];
        }
        int a = arr[idx];
        int b = LcmOfArray(arr, idx+1);
        return (a*b/__gcd(a,b)); // __gcd(a,b) is inbuilt library function
    }

  static void Main() {
    int[] arr = {1,2,8,3};
    Console.WriteLine(LcmOfArray(arr, 0));
    int[] arr1 = {2,7,3,9,4};
    Console.WriteLine(LcmOfArray(arr1,0));
  }
}

Javascript

<script>

    // Function to return
    // gcd of a and b
    function __gcd(a, b)
    {
        if (a == 0)
            return b;
        return __gcd(b % a, a);
    }

    //recursive implementation
    function LcmOfArray(arr, idx){
        // lcm(a,b) = (a*b/gcd(a,b))
        if (idx == arr.length-1){
            return arr[idx];
        }
        let a = arr[idx];
        let b = LcmOfArray(arr, idx+1);
        return (a*b/__gcd(a,b)); // __gcd(a,b) is inbuilt library function
    }

    let arr = [1,2,8,3];
    document.write(LcmOfArray(arr, 0) + "</br>");
    arr = [2,7,3,9,4];
    document.write(LcmOfArray(arr,0));

// This code is contributed by decode2207.
</script>

Output

24
252

Time Complexity: O(n * log(max(a, b)), where n represents the size of the given array.
Auxiliary Space: O(n) due to recursive stack space. 

Method 3: This code uses the reduce function from the functools library and the gcd function from the math library to find the LCM of a list of numbers. The reduce function applies the lambda function to the elements of the list, cumulatively reducing the list to a single value (the LCM in this case). The lambda function calculates the LCM of two numbers using the same approach as the previous implementation. The final LCM is returned as the result.

C++

#include <iostream>
#include <vector>
#include <numeric> // for std::accumulate

int gcd(int a, int b)
{
    if (b == 0)
        return a;
    return gcd(b, a % b);
}

int lcm(std::vector<int> numbers)
{
    return std::accumulate(numbers.begin(), numbers.end(), 1,
        [](int x, int y) { return (x * y) / gcd(x, y); });
}

int main()
{
    std::vector<int> numbers = {2, 3, 4, 5};
    int LCM = lcm(numbers);
    std::cout << "LCM of " << numbers.size() << " numbers is " << LCM << std::endl;
    return 0;
}

Java

// Java code to find LCM of given numbers using reduce()
// function
import java.util.*;
import java.util.function.*;
import java.util.stream.*;

class Main {
    static int lcm(List<Integer> numbers)
    {
        return numbers.stream().reduce(
            1, (x, y) -> (x * y) / gcd(x, y));
    }

    static int gcd(int a, int b)
    {
        if (b == 0)
            return a;
        return gcd(b, a % b);
    }

    public static void main(String[] args)
    {
        List<Integer> numbers = Arrays.asList(2, 3, 4, 5);
        int LCM = lcm(numbers);
        System.out.println("LCM of " + numbers + " is "
                           + LCM);
    }
}

Python3

from functools import reduce
import math

def lcm(numbers):
    return reduce(lambda x, y: x * y // math.gcd(x, y), numbers, 1)

numbers = [2, 3, 4, 5]
print("LCM of", numbers, "is", lcm(numbers))

C#

using System;
using System.Linq;

class Program
{
    static int Lcm(int[] numbers)
    {
        return numbers.Aggregate((x, y) => x * y / Gcd(x, y));
    }

    static int Gcd(int a, int b)
    {
        if (b == 0)
            return a;
        return Gcd(b, a % b);
    }

    static void Main()
    {
        int[] numbers = { 2, 3, 4, 5 };
        int lcm = Lcm(numbers);
        Console.WriteLine("LCM of {0} is {1}", string.Join(", ", numbers), lcm);
    }
}

Javascript

function lcm(numbers) {
  function gcd(a, b) {
    // If the second argument is 0, return the first argument (base case)
    if (b === 0) {
      return a;
    }
    // Otherwise, recursively call gcd with arguments b and the remainder of a divided by b
    return gcd(b, a % b);
  }
  // Reduce the array of numbers by multiplying each number together and dividing by their gcd
  // This finds the Least Common Multiple (LCM) of the numbers in the array
  return numbers.reduce((a, b) => a * b / gcd(a, b));
}

// array
let numbers = [2, 3, 4, 5];

// Call the lcm function
let lcmValue = lcm(numbers);

// Print the Output
console.log(`LCM of ${numbers.join(', ')} is ${lcmValue}`);

Output

LCM of 4 numbers is 60

The time complexity of the program is O(n log n)

The auxiliary space used by the program is O(1) 

Method 4: Using Euclidean algorithm 

The function starts by initializing the lcm variable to the first element in the array. It then iterates through the rest of the array, and for each element, it calculates the GCD of the current lcm and the element using the Euclidean algorithm. The calculated GCD is stored in the gcd variable.

Once the GCD is calculated, the LCM is updated by multiplying the current lcm with the element and dividing by the GCD. This is done using the formula LCM(a,b) = (a * b) / GCD(a,b).

C++

#include <iostream>
#include <vector>
using namespace std;

int gcd(int num1, int num2)
{
    if (num2 == 0)
        return num1;
    return gcd(num2, num1 % num2);
}

int lcm_of_array(vector<int> arr)
{
    int lcm = arr[0];
    for (int i = 1; i < arr.size(); i++) {
        int num1 = lcm;
        int num2 = arr[i];
        int gcd_val = gcd(num1, num2);
        lcm = (lcm * arr[i]) / gcd_val;
    }
    return lcm;
}

int main()
{
    vector<int> arr1 = { 1, 2, 8, 3 };
    vector<int> arr2 = { 2, 7, 3, 9, 4 };
    cout << lcm_of_array(arr1) << endl; // Output: 24
    cout << lcm_of_array(arr2) << endl; // Output: 252
    return 0;
}

Java

import java.util.*;

public class Main {

    public static int gcd(int num1, int num2)
    {
        if (num2 == 0)
            return num1;
        return gcd(num2, num1 % num2);
    }

    public static int lcm_of_array(ArrayList<Integer> arr)
    {
        int lcm = arr.get(0);
        for (int i = 1; i < arr.size(); i++) {
            int num1 = lcm;
            int num2 = arr.get(i);
            int gcd_val = gcd(num1, num2);
            lcm = (lcm * arr.get(i)) / gcd_val;
        }
        return lcm;
    }

    public static void main(String[] args)
    {
        ArrayList<Integer> arr1
            = new ArrayList<>(Arrays.asList(1, 2, 8, 3));
        ArrayList<Integer> arr2
            = new ArrayList<>(Arrays.asList(2, 7, 3, 9, 4));
        System.out.println(
            lcm_of_array(arr1)); // Output: 24
        System.out.println(
            lcm_of_array(arr2)); // Output: 252
    }
}

Python3

def lcm_of_array(arr):
    lcm = arr[0]
    for i in range(1, len(arr)):
        num1 = lcm
        num2 = arr[i]
        gcd = 1
        # Finding GCD using Euclidean algorithm
        while num2 != 0:
            temp = num2
            num2 = num1 % num2
            num1 = temp
        gcd = num1
        lcm = (lcm * arr[i]) // gcd
    return lcm


# Example usage
arr1 = [1, 2, 8, 3]
arr2 = [2, 7, 3, 9, 4]
print(lcm_of_array(arr1))  # Output: 24
print(lcm_of_array(arr2))  # Output: 252

C#

using System;
using System.Collections.Generic;

class Program {
    static int Gcd(int num1, int num2)
    {
        if (num2 == 0)
            return num1;
        return Gcd(num2, num1 % num2);
    }

    static int LcmOfArray(List<int> arr)
    {
        int lcm = arr[0];
        for (int i = 1; i < arr.Count; i++) {
            int num1 = lcm;
            int num2 = arr[i];
            int gcdVal = Gcd(num1, num2);
            lcm = (lcm * arr[i]) / gcdVal;
        }
        return lcm;
    }

    static void Main()
    {
        List<int> arr1 = new List<int>{ 1, 2, 8, 3 };
        List<int> arr2 = new List<int>{ 2, 7, 3, 9, 4 };
        Console.WriteLine(LcmOfArray(arr1)); // Output: 24
        Console.WriteLine(LcmOfArray(arr2)); // Output: 252
    }
}

Javascript

function gcd(num1, num2) {
    if (num2 == 0)
        return num1;
    return gcd(num2, num1 % num2);
}

function lcm_of_array(arr) {
    let lcm = arr[0];
    for (let i = 1; i < arr.length; i++) {
        let num1 = lcm;
        let num2 = arr[i];
        let gcd_val = gcd(num1, num2);
        lcm = (lcm * arr[i]) / gcd_val;
    }
    return lcm;
}

let arr1 = [1, 2, 8, 3];
let arr2 = [2, 7, 3, 9, 4];
console.log(lcm_of_array(arr1)); // Output: 24
console.log(lcm_of_array(arr2)); // Output: 252

Output

24
252

The time complexity of the above code is O(n log n), where n is the length of the input array. This is because for each element of the array, we need to find the GCD, which has a time complexity of O(log n) using the Euclidean algorithm. Since we are iterating over n elements of the array, the overall time complexity becomes O(n log n).

The auxiliary space used by this algorithm is O(1), as only a constant number of variables are used throughout the algorithm, regardless of the size of the input array.

If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above